线性回归

概念

---

　　回归即Regression，回归分析到意思中其实包含了“倒推”的含义，其实就是一种归纳到过程，一种思想。当看到大量事实所呈现的样式形态，推断出原因是如何的；当看到大量到数字对(pair)是某种样态，推断他们之间蕴含到关系是如何的。

　　线性回归是利用数理统计学中到回归分析来确定两种或者两种以上变量间相互依赖到定量关系到一种统计分析方法。先不讲概念，我直接用例子说明吧。

　　我们知道两个点可以确定一条直线，那么假设平面内有n个点，我们画一条线使得这个线尽量的代表这个点的分布，那么该如何画呢？

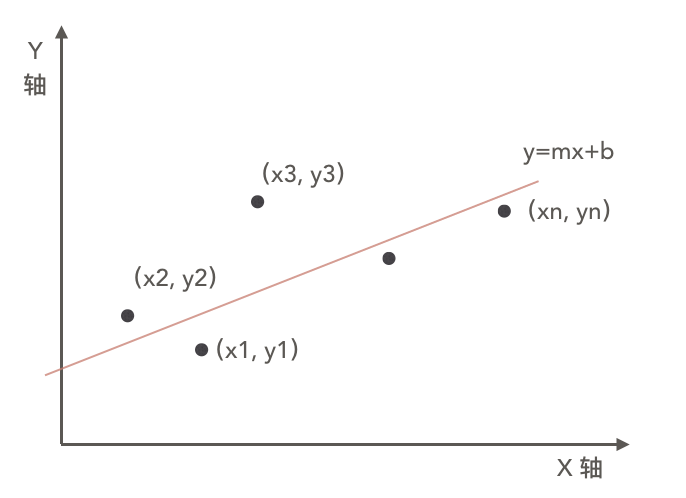
推导过程

---

　　接下来部分我就用图了，因为公式实在很难打出来：

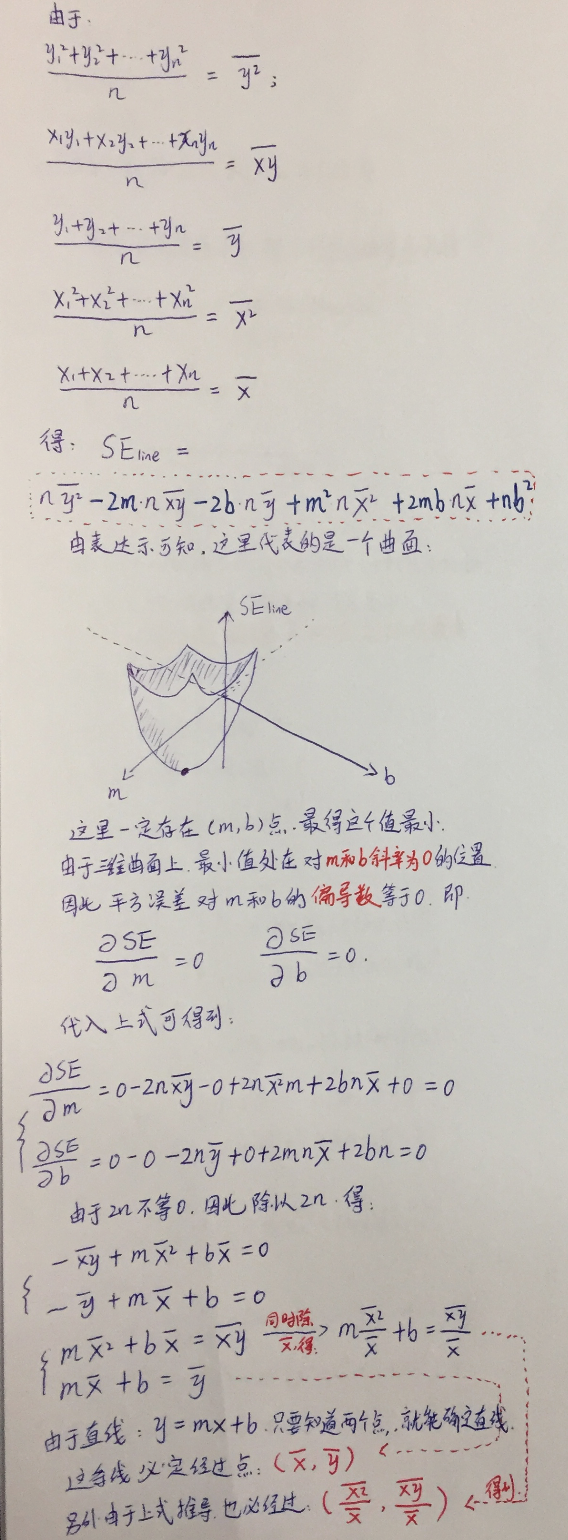
　　通过上面的推断，最终得到的最佳拟合直线的 斜率和截距。

　　斜率：m = （（x平均*y平均）–（x*y）的平均）÷（（x平均）*（x平均）–（x²）的平均）

　　截距：b = y平均 – m*x平均

　　

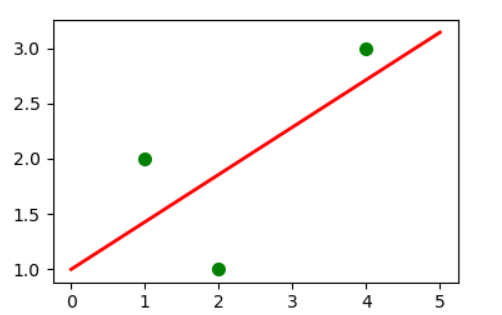
　　接下来，我们就用一个实际的例子来验证下我们的结果，假设有三个点（1，2）（2，1）（4，3）

　　那么根据上面得知：

　　x平均 = （1+2+4）/3 = 7/3

　　y平均 = （2+1+3）/3 = 2

 　（x*y）的平均 = （1*2+2*1+4*3）/3 = 16/3

　 （x²）的平均 = （1*1+2*2+4*4）/3 = 7

　　所以：

　　m = （（7/3）*2 – 16/3）/（（7/3）*（7/3）– 7）=  3/7

　　b =  y平均 – m*x平均 = 2 – （ 3/7）*（7/3） = 1

　　最终得到的直线方程是：

　　y = （3/7）x + 1

代码实现

---

　　接下来我用python使用最小二乘法将线进行拟合 

# -*- coding:utf-8 -*-
##科学计算库 
import numpy as np   
##绘图库
import matplotlib.pyplot as plt  

# 传入坐标
inputX = [1, 2, 4]
inputY = [2, 1, 3]

##样本数据(Xi,Yi)，需要转换成数组(列表)形式 ，画点用
Xi=np.array(inputX)
Yi=np.array(inputY)

#画样本点
plt.scatter(Xi, Yi, color="green", label="data", linewidth=2) 

# 一次多项式拟合，相当于线性拟合
m, b = np.polyfit(inputX, inputY, 1) 
print ('斜率为：' + str(m) + '
截距为：'+str(b))

#画拟合直线
x = np.linspace(0,5,100) ##在0-15直接画100个连续点
##函数式
y = m*x+b ##函数式
plt.plot(x, y, color="red" ,label="line", linewidth=2) 
plt.show()

　　最终对输出结果为：

斜率为：0.42857142857142877
截距为：0.9999999999999993

　　画出的图像为：