[排序N大件之]谢尔排序

这个我们跳过，好不好

答案是不行啊，学着看一个乐呵吧。

不过从这里开始，让我第一次接触一个排序中的分治概念吧，后面归并排序和快速排序都需要，谢尔排序本质上就是一个对子列表的一个插入排序

当每一个子列表逐渐有序时，最后维持整个列表的有序，付出的代价也会更小

谢尔排序需要一个gap，这个就是每个子列表中，每个元素的间隔，如果是采用二分的思想去构造子列表

第一个gap = len(nums) // 2时，就会有len(nums) //2 个列表，子列表中每个元素的间隔为len(nums) // 2，每个子列表中有1~2~3个元素

把gap在缩短一半，就会重新产生gap//2个列表，子列表中每个元素的间隔为gap//2， 每个子列表中多多少个元素呢？我猜是大概是4个或5个吧

当gap等于1时，那个就会产生一个子列表，那么当前子列表就是整个列表了，元素间隔为1，每个子列表中有len(nums)个元素

谢尔排序还需要每个子列表的位置，用来作为每个子列表进行排序的初始位置

是不是有点晕了？我也有一点，画个图的话大概就是下面那个样子

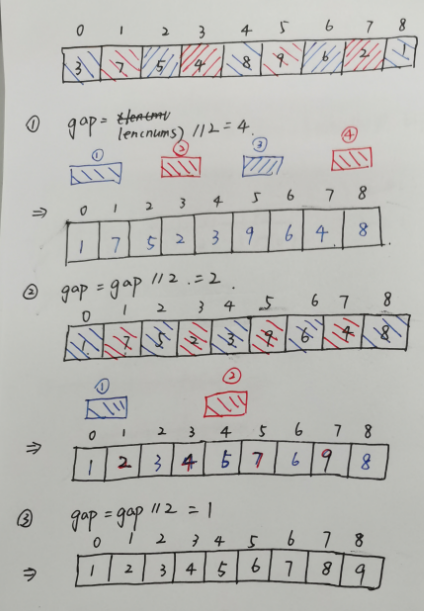
所以只要把子列表构造好，传入每个列表的起始位置和gap值分别进行插入排序，谢尔排序就完成了

def shellSort(nums):

    gap = len(nums) // 2
    while gap > 0:
        for i in range(gap):
            subInsertionSort(nums, i, gap)

        gap = gap // 2

    return nums

def subInsertionSort(nums, start_index, gap):

    for i in range(start_index + 1, len(nums), gap):
        cur = nums[i]
        position = i
        while position >= gap and nums[position - gap] > cur:
            nums[position] = nums[position - gap]
            position = position - gap

        nums[position] = cur

if __name__ == "__main__":
    numbers = [3, 7, 5, 4, 8, 9, 6, 2, 1]
    print(shellSort(numbers))

时间复杂度：O(nlogn) ~ O(nlog²n)

空间复杂度：O(1)