最大子数组和问题求解:
对于这个问题,一下就可以想到一个O(n2)的算法,即穷举连续数组段的首尾索引,两个for解决问题。但还有没有更快的方法呢?答案是肯定的,下面就给出一个时间复杂度为O(n)的算法。
该算法是基于动态规划思想的,我们考虑数组(arr[])中以 i 为结尾的连续数据的的最大值,并用max_arr[]来记录这个最大值。显然,对于 i=0,最大值就是arr[0],即max_arr[0]=arr[0],那对于 i>0 的情况呢?显然max_arr[i]的值受到max_arr[i-1]的值的影响(这正是动态规划思想的体现:将之前计算的结果保留下来用以计算之后的结 果),如果max_arr[i-1]>0(等不等于0无所谓,看具体要求),则max_arr[i]=max_arr[i-1]+arr[i],否 则max_arr[i]=arr[i],除了这两种情况别无其他。于是我们得到了下面这个递推关系:
max_arr[i]= arr[i],i=0或max_arr[i-1]>=0
max_arr[i-1]+arr[i],其他情况
根 据该递推关系,我们就可以得到最大的子数组和了,但还有一个小问题:这样我们只能的到最终的结果值,却不能的到相应的子数组,那有没有办法将子数组也找出 来呢?显然是可以的。我们可以在申请一个数组来保存以 i 结尾的子数组取得最大值时最开始的索引(相对于原数组),而不难得出该数组(max_startindex_arr)满足以下递推关系:
max_startindex_arr=0,i=0
max_startindex_arr[i]=max_startindex_arr[i-1],max_arr[i-1]>=0
max_startindex_arr[i]=i,其他情况
这样我们便记录了所有所需的信息,问题便迎刃而解了,当然这里的最大子数组不唯一,可能有多个,不过根据上面记录的信息,我们都可以把他们找出来。下面给出一种C++实现:
平台:WindowsVisual Studio
语言:C++
输入:保存在文件中,第一行是一个数字N加一个英文逗号",",表征输入数据的个数;第二行有N个数字,以英文
逗号隔开,作为输入的原始数组。
输入样例:6,
5,6,-3,8,-9,2
输出:输出到屏幕,格式如下:
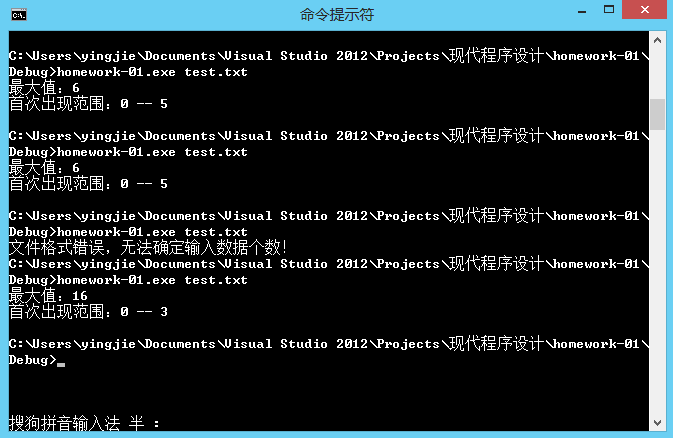
最大值:16
首次出现范围:0 -- 3
其中,最大值是最大子数组和,首次出现范围是产生第一个最大值的子数组索引范围。
运行方法:在cmd中运行:程序可执行文件名+存放输入数据的文件全路径或相对路径。
测试用例:

输出结果:
源代码:
//下面程序针对一维数组一维数组 #include<iostream> #include<fstream> using namespace std; int find_max(int *src_arr,int *max_arr,int *max_startindex_arr,int len){ int max_index=0; for (int i = 1; i < len; i++) { if (max_arr[i-1]>=0) { max_arr[i]=max_arr[i-1]+src_arr[i]; max_startindex_arr[i]=max_startindex_arr[i-1]; if (max_arr[i]>max_arr[max_index]) { max_index=i; } }else { max_arr[i]=src_arr[i]; max_startindex_arr[i]=i; if (max_arr[i]>max_arr[max_index]) { max_index=i; } } } return max_index; } int main(int argc,char *argv[]){ int element_num=-1; //数组元素个数 int max_index=0; //最大值索引 char tmp; ifstream my_cin; int *src_arr; //输入数据数组 int *max_arr; //保存当前最大值的数组 int *max_startindex_arr; //保存最大值范围的起始索引 if(argc!=2){ cout<<"命令行格式错误!"; return 0; }else{ my_cin.open(argv[1]); } if(!my_cin.is_open()){ cout<<"打开输入文件失败!"; return 0; }else{ if(!(my_cin >> element_num)){ cout<<"文件格式错误,无法确定输入数据个数!"; my_cin.close(); return 0; } if(element_num==0){ cout<<"原始数据个数为0!"; my_cin.close(); return 0; } src_arr = new int[element_num]; max_arr = new int[element_num]; max_startindex_arr = new int[element_num]; for (int i = 0; i < element_num; i++) { my_cin>>tmp; if (tmp!=','||!(my_cin>>src_arr[i])) { cout<<"文件格式错误!"; my_cin.close(); return 0; } } my_cin.close(); max_arr[0]=src_arr[0]; max_startindex_arr[0]=0; } max_index = find_max(src_arr,max_arr,max_startindex_arr,element_num); cout<<"最大值:"<<max_arr[max_index]<<endl; cout<<"首次出现范围:"<<max_startindex_arr[max_index]<<" -- "<<max_index<<endl; return 0; }
从上面的代码可以看出:其实核心代码没有几行,大量的代码都是一些容错性处理。当然,可能还是有许多错误不能处理,就比如结果溢出,这些准备在下一次作业中进行处理。当然,要想支持任意大整数,如果不利用语言特性(如python、java对任意大数据的支持),恐怕还是有点难度的。另外,由一维数组的求解过程,我们也很容易联想到二维数组的求解算法,可以在O(mn)的时间内解决问题,这个就留给下次作业了。
另外:我所使用的教科书是《代码大全》。