众所周知,Dijkstra算法是跑单源最短路的一种优秀算法,不过他的缺点在于难以处理负权边。
但是由于在今年的NOI赛场上SPFA那啥了(嗯就是那啥了),所以我们还是好好研究一下Dij的原理和它的优化吧。
(前面那篇写的太简陋了)
1.Dijkstra算法的原理
首先,我们先假设整个图已经被建完而且所有边权全部为正。使用dis[i]表示从原点s到i点的最短距离。之后我们从选取的原点s开始,进行到汇点t的最短路搜寻。s一开始就会连向几个顶点,它所能到达的顶点的距离我们更新一
下,而不能到达的顶点的距离就先设为INF。之后,我们在这个点所能到达的所有点之中,找出一个dis最小的点,那么此时,到这个点的最短路径就已经被确定了。
这是为什么呢?因为图中所有边权全部为正,而当前点(u)的dis已经是最小的了,从其他点(v)再到这个点,所经过的距离必然大于dis[u],也就是肯定不是到达u点的最短路。
因此这样我们就可以不断地确定一些点,之后再从确定的点集出发,去确定更多的点,这样就可以找到到汇点t的最短路径长度了。
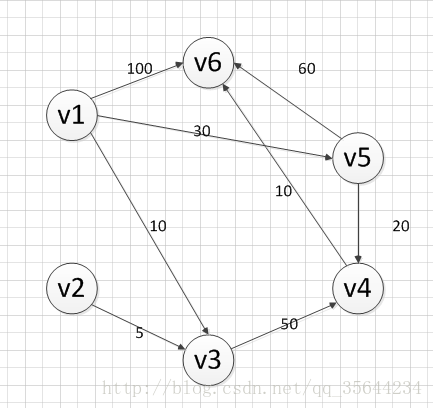
(我偷了别人的图和文章来演示如何求从顶点v1到其他各个顶点的最短路径)
首先第一步,我们先声明一个dis数组,该数组初始化的值为:
我们的顶点集T的初始化为:T={v1}
既然是求 v1顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后,dis[2](下标从0开始)的值就已经从“估计值”变为了“确定值”,即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。
为什么呢?因为目前离 v1顶点最近的是 v3顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.
OK,既然确定了一个顶点的最短路径,下面我们就要根据这个新入的顶点V3会有出度,发现以v3 为弧尾的有: < v3,v4 >,那么我们看看路径:v1–v3–v4的长度是否比v1–v4短,其实这个已经是很明显的了,因为dis[3]代表的就是v1–v4的长度为无穷大,而v1–v3–v4的长度为:10+50=60,所以更新dis[3]的值,得到如下结果:
因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3],通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程。
然后,我们又从除dis[2]和dis[0]外的其他值中寻找最小值,发现dis[4]的值最小,通过之前是解释的原理,可以知道v1到v5的最短距离就是dis[4]的值,然后,我们把v5加入到集合T中,然后,考虑v5的出度是否会影响我们的数组dis的值,v5有两条出度:< v5,v4>和 < v5,v6>,然后我们发现:v1–v5–v4的长度为:50,而dis[3]的值为60,所以我们要更新dis[3]的值.另外,v1-v5-v6的长度为:90,而dis[5]为100,所以我们需要更新dis[5]的值。更新后的dis数组如下图:
然后,继续从dis中选择未确定的顶点的值中选择一个最小的值,发现dis[3]的值是最小的,所以把v4加入到集合T中,此时集合T={v1,v3,v5,v4},然后,考虑v4的出度是否会影响我们的数组dis的值,v4有一条出度:< v4,v6>,然后我们发现:v1–v5–v4–v6的长度为:60,而dis[5]的值为90,所以我们要更新dis[5]的值,更新后的dis数组如下图:
然后,我们使用同样原理,分别确定了v6和v2的最短路径,最后dis的数组的值如下:
那么原理我们就说完了。
2.Dijkstra堆优化
Dijkstra的功能虽然强大,不过其时间复杂度比较大,对于n个点,每次最坏要枚举n次,时间复杂度是O(n^2)的。
这个复杂度有点大,我们考虑如何来优化呢?
首先,Dijkstra是基于贪心的,他每次都是找当前dis值最小的那一个点来继续更新。这样的话,每次的枚举就显得无用,我们直接维护当前最小值就可以了!所以优化就是使用set(小根堆)维护最小值,之后每次在贪心的时候取堆首元素,再更新堆首元素所能走到的点。每次更新的时候,把原来点存储的信息从set里面删掉,再压一个新的进去就可以了。时间复杂度被优化为O(nlogn)。
代码看下面的例题吧。
3.最短路计数
洛谷上的这道题比较简单,因为是无权图(其实有权也一样)。
非常easy的操作,正常跑一遍Dijkstra的堆优化,在每次松弛操作的时候,如果dis[u] > dis[v] + 1,那么到达u的最短路个数应该和到达v是一样的。如果dis[u] = dis[v] + 1,那么到达v的最短路个数应该加上到达u的最短路个数。
因为所有边的边权都是1,所以如果dis[u] = dis[v]+1,那么肯定从u经过的最短路,在v上经过的时候也是最短路。
这样就可以做了,注意取个模。
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<cmath> #include<set> #include<cstdlib> #include<cctype> #include<queue> #define rep(i,a,n) for(int i = a;i <= n;i++) #define per(i,n,a) for(int i = n;i >= a;i--) #define enter putchar(' ') using namespace std; typedef long long ll; const int M = 1000005; const int mod = 100003; int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') op = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { ans *= 10; ans += ch - '0'; ch = getchar(); } return ans * op; } #define pr pair<int,int> #define mp make_pair set <pr> q; set <pr> :: iterator it; int n,m,ecnt,head[M],x,y,dis[M],num[M]; bool vis[M]; struct node { int next,to; }e[M<<1]; void add(int x,int y) { e[++ecnt].next = head[x]; e[ecnt].to = y; head[x] = ecnt; } void dij(int s) { rep(i,1,n) dis[i] = 2147483646; dis[s] = 0,num[s] = 1; q.insert(mp(dis[s],s)); while(!q.empty()) { pr k = *(q.begin()); q.erase(q.begin()); vis[k.second] = 1; for(int i = head[k.second];i;i = e[i].next) { if(dis[e[i].to] > dis[k.second] + 1) { it = q.find(mp(dis[e[i].to],e[i].to)); if(it != q.end()) q.erase(it); dis[e[i].to] = dis[k.second] + 1; num[e[i].to] = num[k.second]; q.insert(mp(dis[e[i].to],e[i].to)); } else if(dis[e[i].to] == dis[k.second] + 1) { num[e[i].to] += num[k.second]; num[e[i].to] %= mod; } } } } int main() { n = read(), m = read(); rep(i,1,m) x = read(), y = read(), add(x,y), add(y,x); dij(1); rep(i,1,n) printf("%d ",num[i]); return 0; }