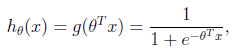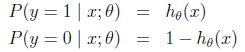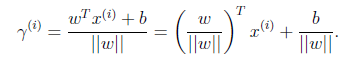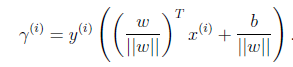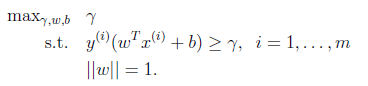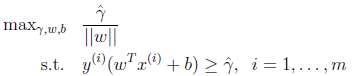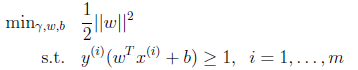SVM(一) 问题的提出

http://www.cnblogs.com/liqizhou/archive/2012/05/11/2495537.html

SVM是支持向量机从诞生至今才10多年，发展史虽短，但其理论研究和算法实现方面却都取得了突破性进展，有力地推动机器学习理论和技术的发展。这一切与支持向量机具有较完备的统计学习理论基础的发展背景是密不可分的。

我看了一下网上的帖子和有关的资料，目前关于SVM大约有3到4个版本，但在网上到处都是转载的内容，最后谁叶不知原稿人是谁。

svm主要分有4个问题

       1.问题的提出

       2.拉格朗日对偶问题。

       3.核函数问题。

       4.二次规划问题。

 1.问题的提出

支持向量机基本上是最好的有监督学习算法了。最开始接触SVM是去年暑假的时候，老师要求交《统计学习理论》的报告，那时去网上下了一份入门教程，里面讲的很通俗，当时只是大致了解了一些相关概念。这次斯坦福提供的学习材料，让我重新学习了一些SVM知识。我看很多正统的讲法都是从VC 维理论和结构风险最小原理出发，然后引出SVM什么的，还有些资料上来就讲分类超平面什么的。这份材料从前几节讲的logistic回归出发，引出了SVM，既揭示了模型间的联系，也让人觉得过渡更自然。

 1.1 重新审视logistic回归

Logistic 回归目的是从特征学习出一个0/1分类模型，而这个模型是将特性的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。因此，使用logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上，映射后的值被认为是属于y=1的概率。

形式化表示就是

假设函数

其中x是n维特征向量，函数g就是logistic函数。

的图像是

 

 

可以看到，将无穷映射到了(0,1)。

而假设函数就是特征属于y=1的概率。

当我们要判别一个新来的特征属于哪个类时，只需求，若大于0.5就是y=1的类，反之属于y=0类。

再审视一下，发现只和有关，>0，那么，g(z)只不过是用来映射，真实的类别决定权还在。还有当(远大于)时，=1，反之=0。如果我们只从出发，希望模型达到的目标无非就是让训练数据中y=1的特征，而是y=0的特征。Logistic回归就是要学习得到，使得正例的特征远大于0，负例的特征远小于0，强调在全部训练实例上达到这个目标。

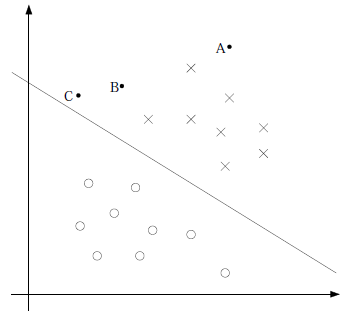
图形化表示如下：

中间那条线是，logistic回顾强调所有点尽可能地远离中间那条线。学习出的结果也就中间那条线。考虑上面3个点A、B和C。从图中我们可以确定A是×类别的，然而C我们是不太确定的，B还算能够确定。这样我们可以得出结论，我们更应该关心靠近中间分割线的点，让他们尽可能地远离中间线，而不是在所有点上达到最优。因为那样的话，要使得一部分点靠近中间线来换取另外一部分点更加远离中间线。我想这就是支持向量机的思路和logistic回归的不同点，一个考虑局部（不关心已经确定远离的点），一个考虑全局（已经远离的点可能通过调整中间线使其能够更加远离）。这是我的个人直观理解。

1.2 形式化表示

我们这次使用的结果标签是y=-1,y=1，替换在logistic回归中使用的y=0和y=1。同时将替换成w和b。以前的，其中认为。现在我们替换为b，后面替换为（即）。这样，我们让，进一步。也就是说除了y由y=0变为y=-1，只是标记不同外，与logistic回归的形式化表示没区别。再明确下假设函数

上一节提到过我们只需考虑的正负问题，而不用关心g(z)，因此我们这里将g(z)做一个简化，将其简单映射到y=-1和y=1上。映射关系如下：

1.3 函数间隔（functional margin）和几何间隔（geometric margin）

给定一个训练样本，x是特征，y是结果标签。i表示第i个样本。我们定义函数间隔如下：

可想而知，当时，在我们的g(z)定义中，，的值实际上就是。反之亦然。为了使函数间隔最大（更大的信心确定该例是正例还是反例），当时，应该是个大正数，反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。

继续考虑w和b，如果同时加大w和b，比如在前面乘个系数比如2，那么所有点的函数间隔都会增大二倍，这个对求解问题来说不应该有影响，因为我们要求解的是，同时扩大w和b对结果是无影响的。这样，我们为了限制w和b，可能需要加入归一化条件，毕竟求解的目标是确定唯一一个w和b，而不是多组线性相关的向量。这个归一化一会再考虑。

刚刚我们定义的函数间隔是针对某一个样本的，现在我们定义全局样本上的函数间隔

 

说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。

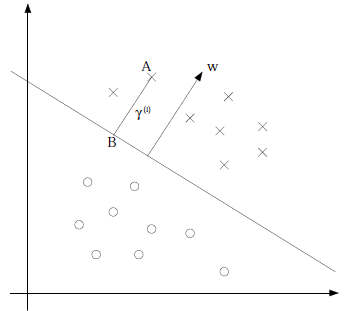
接下来定义几何间隔，先看图

假设我们有了B点所在的分割面。任何其他一点，比如A到该面的距离以表示，假设B就是A在分割面上的投影。我们知道向量BA的方向是（分割面的梯度），单位向量是。A点是，所以B点是x=（利用初中的几何知识），带入得，

进一步得到

实际上就是点到平面距离。

再换种更加优雅的写法：

当时，不就是函数间隔吗？是的，前面提到的函数间隔归一化结果就是几何间隔。他们为什么会一样呢？因为函数间隔是我们定义的，在定义的时候就有几何间隔的色彩。同样，同时扩大w和b，w扩大几倍，就扩大几倍，结果无影响。同样定义全局的几何间隔

1.4  最优间隔分类器（optimal margin classifier）

回想前面我们提到我们的目标是寻找一个超平面，使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面，我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。形象的说，我们将上面的图看作是一张纸，我们要找一条折线，按照这条折线折叠后，离折线最近的点的间距比其他折线都要大。形式化表示为：

这里用=1规约w，使得是几何间隔。

到此，我们已经将模型定义出来了。如果求得了w和b，那么来一个特征x，我们就能够分类了，称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。

由于不是凸函数，我们想先处理转化一下，考虑几何间隔和函数间隔的关系，，我们改写一下上面的式子：

这时候其实我们求的最大值仍然是几何间隔，只不过此时的w不受的约束了。然而这个时候目标函数仍然不是凸函数，没法直接代入优化软件里计算。我们还要改写。前面说到同时扩大w和b对结果没有影响，但我们最后要求的仍然是w和b的确定值，不是他们的一组倍数值，因此，我们需要对做一些限制，以保证我们解是唯一的。这里为了简便我们取。这样的意义是将全局的函数间隔定义为1，也即是将离超平面最近的点的距离定义为。由于求的最大值相当于求的最小值，因此改写后结果为：

这下好了，!!只有线性约束了，而且是个典型的二次规划问题（目标函数是自变量的二次函数）。代入优化软件可解。

到这里发现，这个讲义虽然没有像其他讲义一样先画好图，画好分类超平面，在图上标示出间隔那么直观，但每一步推导有理有据，依靠思路的流畅性来推导出目标函数和约束。

接下来介绍的是手工求解的方法了，一种更优的求解方法。