我们今天来介绍一下B样条曲线。相比较Beizer曲线来说,B样条有着两个优点:(1)k次B样条曲线具有良好的局部性,它只与k+1个控制点有关;(2)B样条曲线拼接较为简单。不过B样条曲线的公式比较难懂,网上介绍原理的也着实不多,这里详细分享一下。
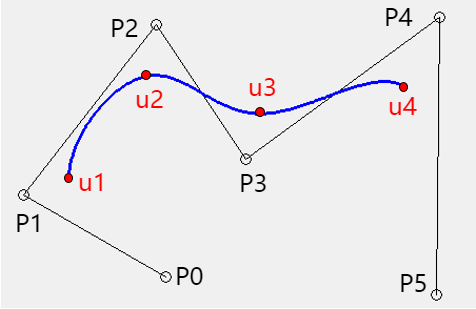
图1
我们先来看看什么是B样条曲线,如图1,我们以三次B样条曲线为例。由于k次B样条曲线的控制点有k+1个,所以P0P1P2P3控制u1u2段曲线,P1P2P3P4控制u2u3段曲线,P2P3P4P5控制u3u4段曲线。所以这样就不会像beizer曲线那样,改变任一控制点,都会对整个曲线产生影响。接下来我们看一下B样条曲线的公式:
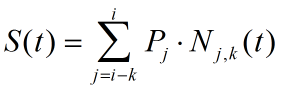
图2
S(t)表示的是uaua+1段曲线,k表示的k次B样条曲线,所以S(t)就是控制点与基函数的乘积之和,其中控制点是从Pj点到Pi点,一共有i-j+1个。结合图1中的u1u2段曲线举个例子,Su1u2(t) = P0N0,3(t) + P1N1,3(t) + P2N2,3(t) + P3N3,3(t)。这个公式比较抽象,我们换种写法,同时我们再给出N(t)的公式:
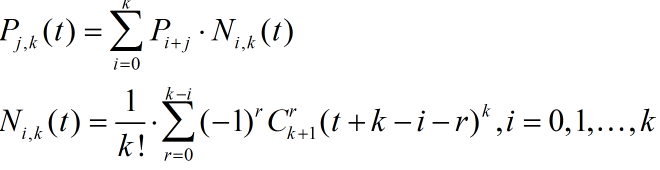
图3
图3、图2的公式参数意义略有不同。图3中,j表示的是起始的控制点,k表示的是k次B样条曲线,i表示的是迭代参数,相当于控制点是从Pj到Pj+k。基函数N(t)中参数i,k跟其上面的公式保持同步。这个公式看起来很复杂,光用文字说明并不能解释太清楚,我们举一个二次B样条曲线和一个三次B样条曲线的例子来说明一下。
(1)二次B样条曲线:k=2,下面是二次B样条曲线的三个基函数(建议大家拿笔算一算,这样对公示理解的更深):
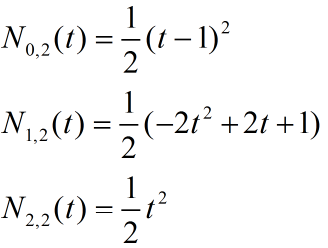
图4
这里我们跟据上面的基函数给出P0,2(t)的公式及相关性质:
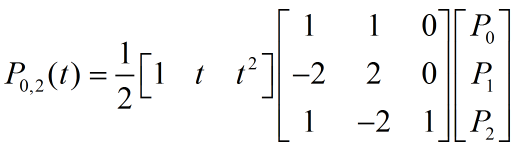 图5
图5
这条曲线的端点位置和端点切失如下:
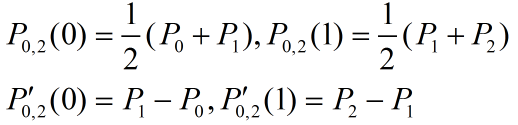
图6
根据上面的公式和性质可以得到如下曲线:
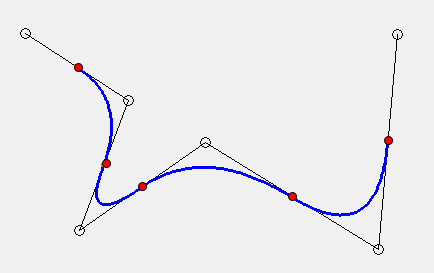
图7
(2)三次B样条曲线:k=3,这个也是我们今天代码展示的曲线。下面是三次B样条曲线的四个基函数:
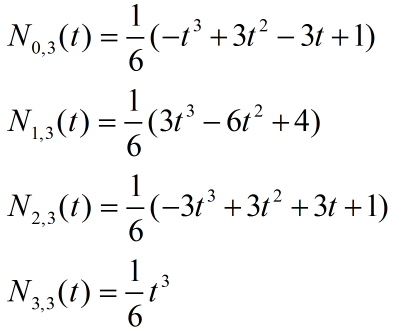 图8
图8
这里我们跟据上面的基函数给出P0,3(t)的公式及相关性质:
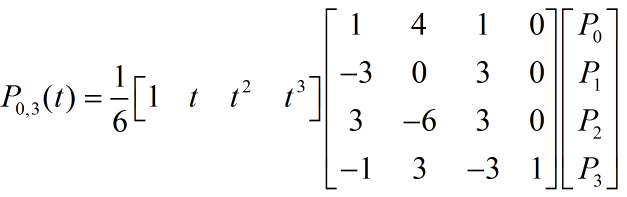
图9
这条曲线的端点位置和端点切失如下:
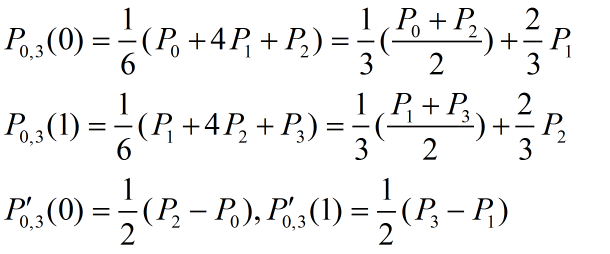
图10
根据上面的公式和性质可以得到如下曲线:
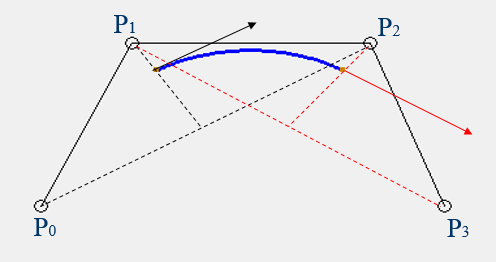
图11
我们这里就讲完三种最基本也是最常用的曲线,我们在贴B样条曲线的代码之前,先讨论一下三种曲线的优缺点(这只是个人观点)。首先,Hermite曲线和Beizer曲线基本是一致的,虽然原理上有着一定的差异,但从性质以及参数的影响程度来说,大致上是相似的。而且这两种曲线在表达复杂的曲线时,都是利用低次曲线拼接的方式来表达。相比这两种曲线,B样条曲线就显得比较具有优势,具体优势开头也有提到,这里就不重复了,缺点也非常明显,控制点不在曲线上导致不好容易控制。
说到这,OpenGL绘制曲线就正式完结了。最后贴出三次B样条曲线的代码(效果就是图1,不过可以拖动顶点调整曲线),大家可以试试。
#include <math.h>
#include <gl/glut.h>
#include <iostream>
using namespace std;
#define NUM_POINTS 6
#define NUM_SEGMENTS (NUM_POINTS-3)
struct Point2
{
double x;
double y;
Point2() { ; }
Point2(int px, int py) { x = px; y = py; }
void SetPoint2(int px, int py) { x = px; y = py; }
};
/*全局变量*/
Point2 vec[NUM_POINTS];
bool mouseLeftDown = false;
/*绘制B样条曲线*/
void Bspline(int n)
{
float f1, f2, f3, f4;
float deltaT = 1.0 / n;
float T;
glBegin(GL_LINE_STRIP);
for (int num = 0; num < NUM_SEGMENTS; num++)
{
for (int i = 0; i <= n; i++) {
T = i * deltaT;
f1 = (-T*T*T + 3*T*T - 3*T + 1) / 6.0;
f2 =(3*T*T*T - 6*T*T + 4) / 6.0;
f3 = (-3*T*T*T +3*T*T + 3*T + 1) / 6.0;
f4 = (T*T*T) / 6.0;
glVertex2f( f1*vec[num].x + f2*vec[num+1].x + f3*vec[num+2].x + f4*vec[num+3].x,
f1*vec[num].y + f2*vec[num+1].y + f3*vec[num+2].y + f4*vec[num+3].y);
}
}
glEnd();
}
void display()
{
glClear(GL_COLOR_BUFFER_BIT);
glLoadIdentity();
glLineWidth(1.5f);
glColor3f(1.0,0.0,0.0);
glBegin(GL_LINE_STRIP);
for(int i = 0;i < NUM_POINTS; i++)
{
glVertex2f(vec[i].x, vec[i].y);
}
glEnd();
glPointSize(10.0f);
glColor3f(0.0, 0.0, 1.0);
glBegin(GL_POINTS);
for(int i = 0;i < NUM_POINTS; i++)
{
glVertex2f(vec[i].x, vec[i].y);
}
glEnd();
Bspline(20);
glFlush();
glutSwapBuffers();
}
void init()
{
glClearColor(1.0, 1.0, 1.0, 0.0);
glShadeModel(GL_FLAT);
vec[0].SetPoint2(200, 400);
vec[1].SetPoint2(100, 300);
vec[2].SetPoint2(200, 200);
vec[3].SetPoint2(250, 300);
vec[4].SetPoint2(400, 200);
vec[5].SetPoint2(400, 400);
}
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei)w, (GLsizei)h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, (GLsizei)w, (GLsizei)h, 0.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void mouse(int button, int state, int x, int y)
{
if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN)
{
mouseLeftDown = true;
}
if (button == GLUT_LEFT_BUTTON && state == GLUT_UP)
{
mouseLeftDown = false;
}
}
double distance(int x1, int y1, int x2, int y2)
{
return sqrt((x1-x2) * (x1 -x2) + (y1-y2) * (y1-y2));
}
void motion(int x, int y)
{
if (mouseLeftDown)
{
for (int i = 0; i < NUM_POINTS; i++)
{
if (distance(vec[i].x, vec[i].y, x, y) < 20)
{
vec[i].SetPoint2(x, y);
}
}
}
glutPostRedisplay();
}
int main(int argc,char** argv)
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_RGBA|GLUT_DOUBLE);
glutInitWindowSize(500, 500);
glutInitWindowPosition (200, 200);
glutCreateWindow("B-Spline Curve");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMouseFunc(mouse);
glutMotionFunc(motion);
glutMainLoop();
return 0;
}