由于图形学比较复杂,经常会遇到各种各样的小问题,这里做一个汇总,方便以后查找。
1、坐标系
一般来说,坐标系分为左手坐标系和右手坐标系。如图1所示,左图为右手坐标系,右图为左手坐标系。两个坐标系通过旋转、平移、缩放这几个操作是没有办法相互转化的。所以在处理顶点等数据的时候,要特别注意这些数据实在什么样的坐标系环境里。比如,我曾经写过一个程序,将3dmax中的模型导入opengl中。由于3dmax是用左手坐标系,而opengl是用右手坐标系,直接导入肯定会出问题。最简单的方法就是变换坐标次序,把<x,y,z>赋给<z,x,y>。
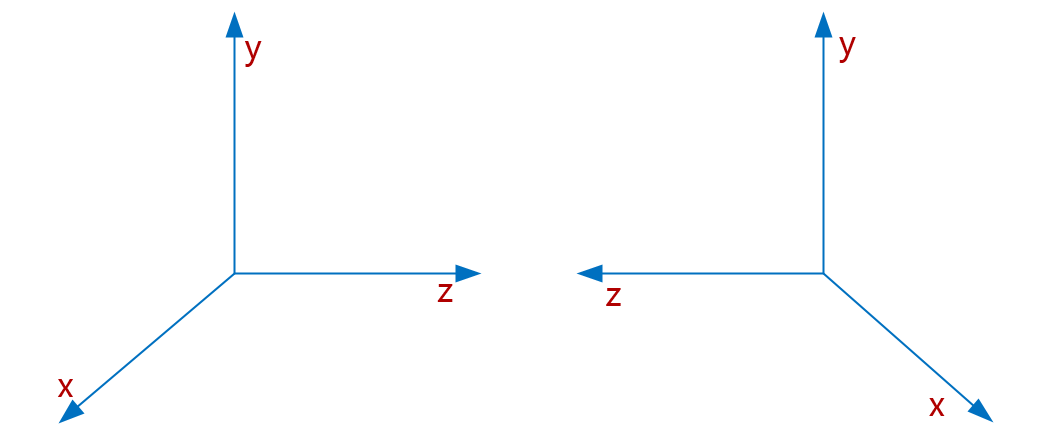
图1
2、行优先和列优先
行优先和列优先也称行主序和列主序,这两概念都是针对二维数组来说的。顾名思义,行主序的意思也就是在存储二维数组的时候,将数据先填满行,再填满列。列主序就是先填满列,再填满行。举个例子,我们这里有一个4*4的二维数组,里面包含16个元素(a1,a2,...,a16)。图2中左图为行主序的存储方式,右图为列主序的存储方式。C++中存储二维数组就是以行主序的方式存储的。那么我们在OpenGl中经常处理一些矩阵,矩阵可以说就是一个二维数组。OpenGL存储矩阵的方式和C++的存储方式正好是相反,它是以列主序的方式存储的。这里再说个例子,OpenGL的shader中也是以列主序的方式存储,不过我们有时不必考虑这一点:当我们使用gluniformmatrix()这个函数传递矩阵的时候,其中有个参数transpose,如果设置为GL_TRUE,那么数据是以行主序的顺序读入,如果是GL_FALSE,那么数据是以列主序的方式读入。所以我建议在自己写矩阵的时候最好以一维数组的方式表达。
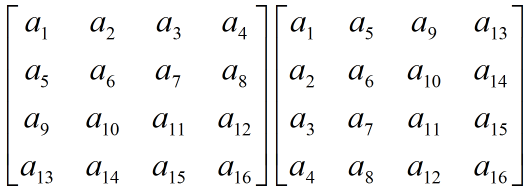
图2
3、矩阵的左乘和右乘
矩阵乘法分为右乘和左乘,由于矩阵乘法不支持交换律,所以左乘和右乘肯定是不一样。其实再我看来,左乘右乘的区别一点也不复杂,就是列主序和行主序的区别。为什么这么说呢?下面我举个例子。变换矩阵T中旋转信息为(r1,r2,...,r9),平移信息为(t1,t2,t3)。图3中上图就是一个右乘的例子,而矩阵就是一个行主序的存储方式,下图就是左乘,矩阵式一个列主序的。这里主要注意的是平移信息的位置的变化,就可以看出左乘和右乘的区别了。OpenGL用列主序的方式存储矩阵,所以OpenGL矩阵都是左乘。另外3dmax也是左乘。
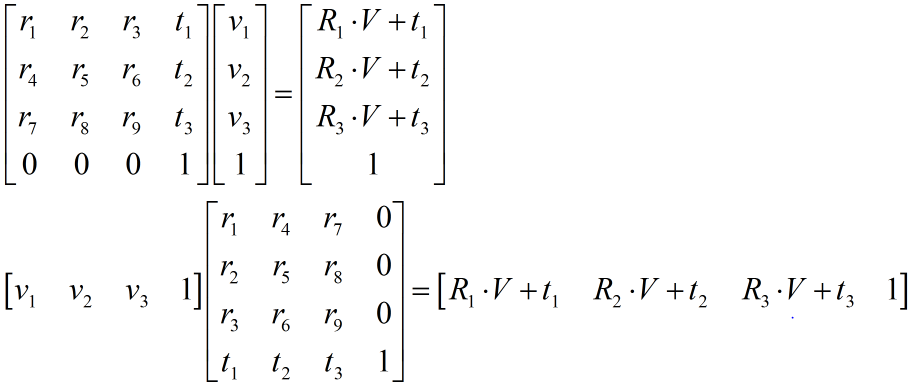
图3