原文链接:https://jiang-hao.com/articles/2020/algorithms-algorithms-insert-sort.html
算法原理
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。(有点像扑克牌在手上排序的过程)
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
排序步骤
将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
动图演示
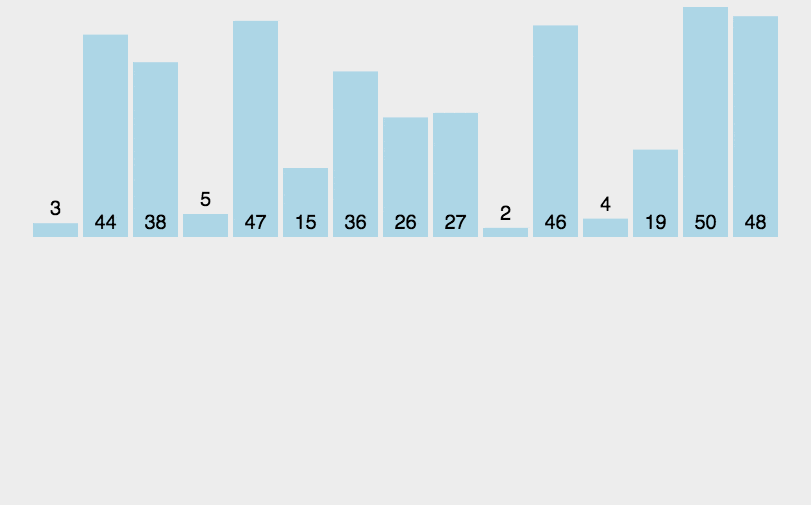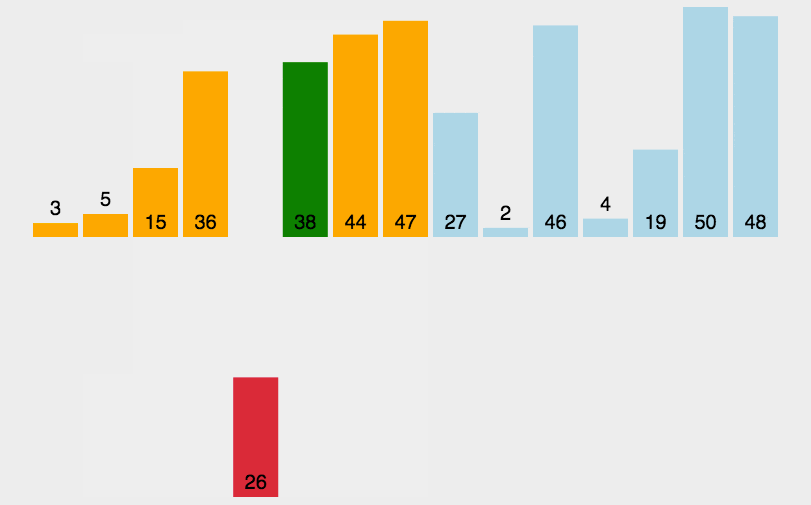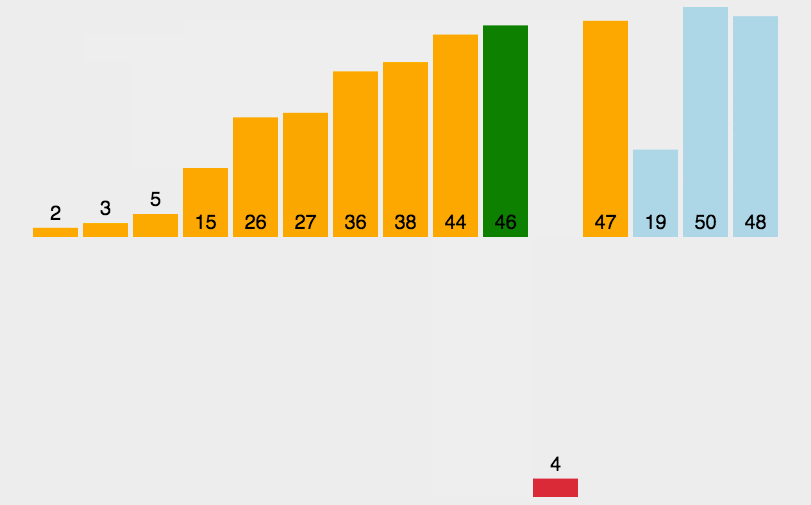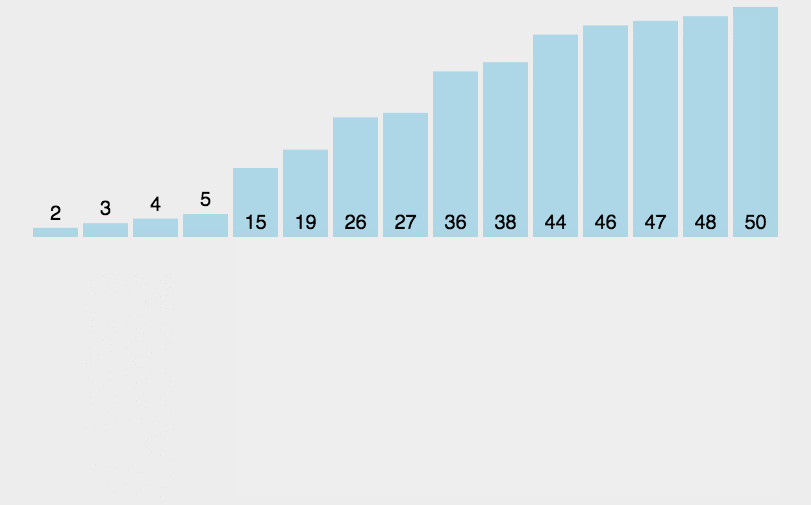
代码实现
public static int[] insert_sort_original(int[] nums) {
int[] arr = Arrays.copyOf(nums, nums.length);
int valuationCnt=0; // 赋值操作计数
int comparisonCnt=0; // 比较操作计数
for (int i=1; i<nums.length; i++) {
int target = arr[i];
int j;
for (j=i; j>0 && target<arr[j-1]; j--) {
valuationCnt++;
comparisonCnt++;
arr[j] = arr[j-1];
}
arr[j] = target;
}
System.out.println(comparisonCnt+ "," +valuationCnt);
return arr;
}
复杂度分析
时间复杂度
在插入排序中,当待排序数组是有序时,是最优的情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较N- 1次,时间复杂度为O(N)。
最坏的情况是待排序数组是逆序的,此时需要比较次数最多,总次数记为:1+2+3+…+N-1,所以,插入排序最坏情况下的时间复杂度为O(N^2)。
空间复杂度
插入排序的空间复杂度为常数阶O(1)。
总结
| 平均时间复杂度 | [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xVXuqLd2-1608381699639)(https://wikimedia.org/api/rest_v1/media/math/render/svg/6cd9594a16cb898b8f2a2dff9227a385ec183392)] |
|---|---|
| 最坏时间复杂度 | [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xtcPXaJ5-1608381699641)(https://wikimedia.org/api/rest_v1/media/math/render/svg/6cd9594a16cb898b8f2a2dff9227a385ec183392)] |
| 最优时间复杂度 | [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gp5n3v6z-1608381699643)(https://wikimedia.org/api/rest_v1/media/math/render/svg/34109fe397fdcff370079185bfdb65826cb5565a)] |
| 空间复杂度 | [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-juHRH2ar-1608381699646)(https://wikimedia.org/api/rest_v1/media/math/render/svg/e66384bc40452c5452f33563fe0e27e803b0cc21)] |
| 稳定性 | 稳定 |
算法优化
折半插入(二分查找)
二分查找插入排序的原理:是直接插入排序的一个变种,区别是:在有序区中查找新元素插入位置时,为了减少元素比较次数提高效率,采用二分查找算法进行插入位置的确定。
public static int[] insert_sort_binary_search(int[] nums) {
int[] arr = Arrays.copyOf(nums, nums.length);
int valuationCnt=0;
int comparisonCnt=0;
for (int i=1; i<nums.length; i++) {
int target = arr[i];
int left = 0;
int right = i;
while (left < right) {
comparisonCnt++;
int middle = left + (right-left)/2;
if (arr[middle] > target) {
right = middle;
} else {
left = middle + 1;
}
}
int j;
for (j=i; j>left; j--) {
valuationCnt++;
arr[j] = arr[j-1];
}
arr[j] = target;
}
System.out.println(comparisonCnt+ "," +valuationCnt);
return arr;
}
优化结果
运行直接插入排序代码和二分插入排序代码,使用数据集https://leetcode-cn.com/submissions/detail/114474973/testcase/测试运行,得结果如下:
622443661,622443661 // 直接插入排序
711424,622443661 // 二分插入排序
可见二分插入排序大大降低了元素的比较次数,其时间复杂度如下:
最好情况:查找的位置是有序区的最后一位后面一位,则无须进行后移赋值操作,其比较次数为:log2n 。即O(log2N)。
最坏情况:查找的位置是有序区的第一个位置,则需要的比较次数为:log2n,需要的赋值操作次数为n(n-1)/2加上 (n-1) 次。即O(N^2)。
平均时间复杂度:O(N^2)。
从实现原理可知,二分查找插入排序是在原输入数组上进行后移赋值操作的(称“就地排序”),所需开辟的辅助空间跟输入数组规模无关,所以空间复杂度为:O(1)。