KL散度、JS散度和交叉熵三者都是用来衡量两个概率分布之间的差异性的指标
1. KL散度
KL散度又称为相对熵,信息散度,信息增益。KL散度是是两个概率分布 P 和 Q (概率分布P(x)和Q(x)) 之间差别的非对称性的度量。 KL散度是用来 度量使用基于 Q 的编码来编码来自 P 的样本平均所需的额外的位元数。 典型情况下,P 表示数据的真实分布,Q 表示数据的理论分布,模型分布,或 P 的近似分布
定义如下:

因为对数函数是凸函数,所以KL散度的值为非负数。
当P(x)和Q(x)的相似度越高,KL散度越小。
KL散度主要有两个性质:
(1)不对称性
尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即D(P||Q)!=D(Q||P)
(2)非负性
相对熵的值是非负值,即D(P||Q)>0
2.JS散度(Jensen-Shannon divergence)
JS散度度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。一般地,JS散度是对称的,其取值是 0 到 1 之间。定义如下:

但是不同于KL主要又两方面:
(1)值域范围
JS散度的值域范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更确切了。
(2)对称性
即 JS(P||Q)=JS(Q||P),从数学表达式中就可以看出
KL散度和JS散度度量的时候有一个问题:
如果两个分配 P,QP,Q 离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为 00。梯度消失了
3.交叉熵(Cross Entropy)
在神经网络中,交叉熵可以作为损失函数,因为它可以衡量P和Q的相似性
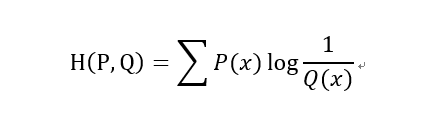
交叉熵和相对熵的关系
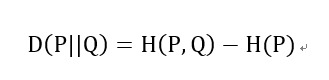
以上都是基于离散分布的概率,如果是连续的数据,则需要对数据进行Probability Density Estimate来确定数据的概率分布,就不是求和而是通过求积分的形式进行计算了