使用Spark进行ALS编程的例子可以看:http://www.cnblogs.com/charlesblc/p/6165201.html
ALS:alternating least squares
关于协同过滤ALS原理的可以看这篇文章:http://www.docin.com/p-938897760.html
最后的惩罚因子那部分没看懂。前面的还挺好的。








上面3.1节关于矩阵分解模型的自然意义和解释,讲的非常好!
注:矩阵的每一行代表一个方程,m行代表m个线性联立方程。 n列代表n个变量。如果m是独立方程数,根据m<n、m=n、m>n确定方程是 ‘欠定’、‘适定’ 还是 ‘超定’。
注:frobenius范数的定义?

矩阵的模:就是矩阵中每个元素的平方和再开方。
下面这篇讲的内容主要是Spark关于ALS的实现,
也很好:http://www.dataguru.cn/article-7049-1.html


我们把一个协同推荐的问题通过低秩假设成功转变成了一个优化问题。下面要讨论的内容很显然:这个优化问题怎么解?其实答案已经在 ALS 的名字里给出——交替最小二乘。(最小二乘法,见下)
ALS 的目标函数不是凸的,而且变量互相耦合在一起,所以它并不算好解。
注:凸函数还有一个重要的性质:对于凸函数来说,局部最小值就是全局最小值。
但如果我们把用户特征矩阵U和产品特征矩阵V固定其一,这个问题立刻变成了一个凸的而且可拆分的问题。比如我们固定U,那么目标函数就可以写成

Spark MLlib的性能很棒:

大家在 Spark 上实现机器学习算法时,不妨先分析一下空间、时间、和通信复杂度,然后合理的利用 Spark 的分区和缓存机制做到高效的实现。
最小二乘法
可以参考:http://blog.csdn.net/lotus___/article/details/20546259
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)- 即采用平方损失函数。
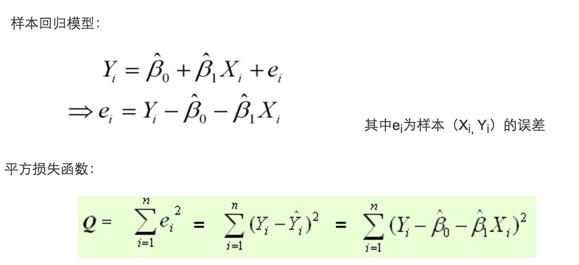

最小二乘法与梯度下降法
最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么区别呢。
相同
1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。
2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为:

不同

上面的所有文章,都是由下面这篇文章看到的:
https://www.zhihu.com/question/31509438/answer/52268608

上面文章里面i 和 j后面加.,指的是只考虑“评过分的”,未评分的不考虑。
其中提到了这篇文章:http://www.docin.com/p-714582034.html 里面的内容明显是山寨的,就不贴了。
重要的是 加正则化参数,来防止过拟合。
总结一下:
ALS算法的核心就是将稀疏评分矩阵分解为用户特征向量矩阵和产品特征向量矩阵的乘积
交替使用最小二乘法逐步计算用户/产品特征向量,使得差平方和最小
通过用户/产品特征向量的矩阵来预测某个用户对某个产品的评分
两个问题
(1)在第一个公式中加入正则化参数是啥意思?为什么是那种形态的?
(2)固定一个矩阵U,求偏导数之后可以得到求解V的公式,为什么?
回答:
(1)加入正则化项朴实点说就是避免分解出的值太大带来过拟合的问题,至于为什么是这种形态,两个原因:a、这样就能很好避免分解出过大值的问题;b、计算求导方便,使得优化容易,同时尽可能减少模型估计误差。
(2)固定一个矩阵求解另一个绝阵,这种方法其实就是坐标梯度下降法的一个变形,这种方法优点是计算优化简单,缺点是收敛略慢,有兴趣可以查看相关资料。
补充:(2):这是多元函数求极值的方法,回想一下最简单的一元函数求极值,就是求其一阶导数等于0的点。而多元函数求极值无非就是求使得每个偏导数等于0的点嘛。但是,每个偏导数等于0是原函数极值点的必要非充分条件。
补充:(1):正则化加入代价函数 L(U,V),求U,V 使 L(U,V) 趋近0则相当于把正则项最小化。这样能够让模型不过拟合,具有更好的普适性。不同的正则化方法,能够达到不同的防过拟合的效果,可以参考正则化用到的 L0 L1 L2 L3距离函数,在2~3维的图像。(注:看起来上面那个是L2正则)
这篇文章对ALS-WR算法有描述,
开始我以为WR指的就是加入最后的正则化项(也叫代价函数,也叫惩罚因子),看起来不完全是。往下看。
http://blog.csdn.net/wguangliang/article/details/51539710
ALS-WR是alternating-least-squares with weighted-λ -regularization的缩写,意为加权正则化交替最小二乘法。
该方法常用于基于矩阵分解的推荐系统中。例如:将用户(user)对商品(item)的评分矩阵分解为两个矩阵:一个是用户对商品隐含特征的偏好矩阵,另一个是商品所包含的隐含特征的矩阵。在这个矩阵分解的过程中,评分缺失项得到了填充,也就是说我们可以基于这个填充的评分来给用户最商品推荐了。
损失函数一般需要加入正则化项来避免过拟合等问题,我们使用L2正则化,所以上面的公式改造为:

到这里,协同过滤就成功转化成了一个优化问题。

- 迭代步骤:首先随机初始化Y,利用公式(3)更新得到X, 然后利用公式(4)更新Y, 直到均方根误差变RMSE化很小或者到达最大迭代次数。
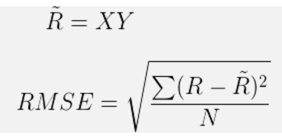
ALS-WR
上文提到的模型适用于解决有明确评分矩阵的应用场景,然而很多情况下,用户没有明确反馈对商品的偏好,也就是没有直接打分,我们只能通过用户的某些行为来推断他对商品的偏好。
比如,在电视节目推荐的问题中,对电视节目收看的次数或者时长,这时我们可以推测次数越多,看得时间越长,用户的偏好程度越高,但是对于没有收看的节目,可能是由于用户不知道有该节目,或者没有途径获取该节目,我们不能确定的推测用户不喜欢该节目。
ALS-WR通过置信度权重来解决这些问题:对于更确信用户偏好的项赋以较大的权重,对于没有反馈的项,赋以较小的权重。ALS-WR模型的形式化说明如下:
