最小生成树模版 Kruskal

如题，简单来说，最小生成树就是给出一定结点和无向边，通过选定给出的无向边把结点连接成一棵或几棵树，使它（它们）的边权最小

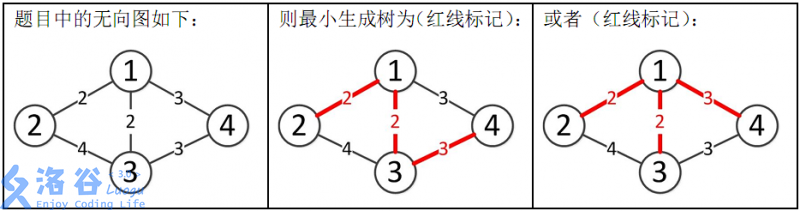
如图所示，该最小生成树的最小边权即为2+2+3=7

最小生成树常用的有两种方法：Prim和Kruskal  

这里只说Kruskal（炒鸡感谢hyc神犇的讲解，讲的真的特别清楚）

先看模版题（传送门）

正好gg周末讲了贪心，其实就是Kruskal的基本思路：先把给定无向边按照权值进行排序，用贪心的思想优先选取权值较小的边，并依次连接，若出现环（无向边两端结点已连接）则跳过此边（用并查集来判断是否存在环）继续搜，直到已经使用的边的数量比

 

同时为方便操作，推荐用结构体储存边权，sort进行快排

 

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,i,j,u,v,total;
struct edge{
    int start,to;long long val;
}bian[2000005];
int f[100000];
long long ans;

int find(int x)
{
    if (f[x]!=x)
    f[x]=find(f[x]);
    return f[x];
       
}

bool cmp(edge a,edge b)
{
    return a.val<b.val;
}

inline void kruskal()
{

    for(int i=1;i<=m;i++)
    {
        u=find(bian[i].start);
        v=find(bian[i].to);
        if(u==v) continue;
            ans+=bian[i].val;
            f[u]=v;
            total++;
            if(total==n-k) break;
    }
} 
int main()
{
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++) f[i]=i;
    for(i=1;i<=m;i++)
    {
        scanf("%d%d%d",&bian[i].start,&bian[i].to,&bian[i].val);
    }
    sort(bian+1,bian+m+1,cmp);
    kruskal();
    printf("%d",ans);
    return 0;
}

再附一道相同思想的题，同样应用了Kruskal：P1195 口袋的天空（很符合诗意科学的一道题）

虽然难度提了两个档，但其实感觉和模版并没有很大的差异，唯一要特别改动的地方是要调整结束连边的条件，因为要生成的可能并不止一棵树。

强力推荐能看到这里的朋友们去看一下hyc神犇的题解讲的真的好%%%

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,k,i,j,u,v,total,sign;
struct edge{
    int start,to,val;
}bian[10010];
int f[1010];
long long ans;

int find(int x)
{
    if (f[x]!=x)
    f[x]=find(f[x]);
    return f[x];
       
}

bool cmp(edge a,edge b)
{
    return a.val<b.val;
}

void kruskal()
{

    for(int i=1;i<=m;i++)
    {
        u=find(bian[i].start);
        v=find(bian[i].to);
        if(u==v) continue;
            ans+=bian[i].val;
            f[u]=v;
            total++;
            if(total==n-k)
            {   sign=1;
                break;}
    }
} 
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(i=1;i<=n;i++) f[i]=i;
    for(i=1;i<=m;i++)
    {
        scanf("%d%d%d",&bian[i].start,&bian[i].to,&bian[i].val);
    }
    sort(bian+1,bian+m+1,cmp);
    kruskal();
    if(sign==1) printf("%d",ans);
    else printf("No Answer");
    return 0;
}