Codeforces Round #642 (Div. 3)

Codeforces #642 (Div. 3)

A. Most Unstable Array

题意：构造序列a,使得(sum_{i=1}^{n} a_{i} = m)，且 (sum_{i = 1}^{n-1}|a_{i} - a_{i + 1}|) 最大。输入n,m，输出这个最大值。

题解：

• n = 1, res = 0。
• n = 2, res = m。
• n > 2, res = m * 2。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 5;

int T, n, m;
int main()
{
    scanf("%d",&T);
    while(T --){
        scanf("%d%d",&n,&m);
        if(n == 1) printf("0
");
        else if(n == 2) printf("%d
",m);
        else printf("%d
",m * 2);
    }
    return 0;
}

B. Two Arrays And Swaps

题意：给两个数组a,b。 可以执行操作：任意交换a数组与b数组中两个数，求不超过k次操作可以得到的A数组的和的最大值。

题解：

题目操作可以理解为把B数组中较大的数交换到A数组中，为了让A数组的和最大，那每次看能否把A中最小值换成B中比它更大的值，这样一定使答案变得更优。显然每次尝试去换B中最大值。

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
const int N = 3e6 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const ll INF = 1e9;

int a[N], b[N];
int T, n, k;
int main()
{
    scanf("%d",&T);
    while(T --){
        scanf("%d%d",&n,&k);
        for(int i = 1; i <= n; ++ i) scanf("%d",&a[i]);
        for(int i = 1; i <= n; ++ i) scanf("%d",&b[i]);
        sort(a + 1, a + n + 1);
        sort(b + 1, b + n + 1, cmp);
        for(int i = 1; i <= k; ++ i)
            if(a[i] < b[i]) a[i] = b[i];
        int res = 0;
        for(int i = 1; i <= n; ++ i) res += a[i];
        printf("%d
",res);
    }
    return 0;
}

C. Board Moves

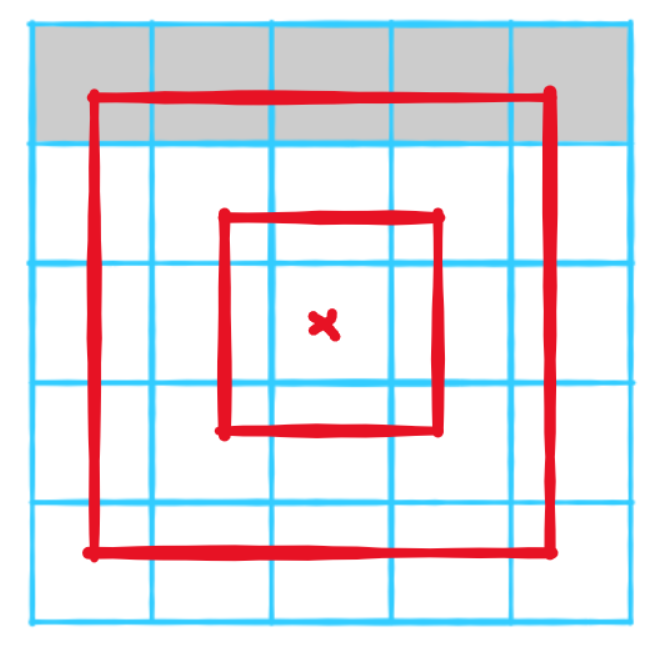
题意： n*n (n为奇数) 的网格图每个格子有一个物品，一次移动可以把这个物品移到周围8个方向的网格中。问把所有物品移到一个格子的最少移动次数。

题解：

把一个物品从一个格子移到另一个格子对答案的贡献是两个格子的哈密顿距离( (|x_{1}-x_{2}|+|y_{1}-y_{2}|​) ) 。那么所有物品移动到最中间距离和最少。

从中间格子开始进行分层，第i层到中间格子的距离是 i - 1, 每层贡献是： (每层格子数 * (i - 1)) 。且除第1和2层外任意相邻两层相差8，当然第1层贡献是0，可以直接从第2层开始计算每层贡献求和就是答案。

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
const int N = 2e5 + 105;
const int mod = 998244353;

ll T, n;
int main()
{
    scanf("%lld",&T);
    while(T --){
        scanf("%lld",&n);
        ll res = 0, num = 8;
        for(ll i = 2; i <= n / 2 + 1; ++ i){
            res += num * (i - 1); 
            num += 8;
        }
        printf("%lld
",res);
    }
    return 0;
}

D. Constructing the Array

题意： 给一个数组，初始时都是0，第 i 次操作你需要找到连续的0最多的区间[l, r]。如果区间大小是奇数，把中间位置 mid 设为 i，如果区间大小是偶数，把(mid = (l + r - 1) / 2) 位设为 i 。输出最后的数组。

题解：

要解决这道题你需要发现：每次操作实际就是找剩下连续0的最大区间。可以用优先队列维护连续0的区间大小，每次操作处理优先队列头的区间[l, r] , 然后把[l, mid - 1]，和[mid + 1, r] 区间放入优先队列。

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
#define px first
#define py second
typedef long long ll;
typedef pair<int,int> PII;
const int N = 5e5 + 5;
const int mod = 1e9 + 7;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
// bool cmp(ll a, ll b){return a > b;}

struct node{
    int l, r, val;
};
bool operator < (node a, node b) {
    if(a.val != b.val) return a.val < b.val;
    else return a.l > b.l;
}  
int T, n, cnt, mid;
int res[N];
int main()
{
    scanf("%d",&T);
    while(T --){
        cnt = 0; memset(res, 0, sizeof(res));
        priority_queue<node> q;
        scanf("%d",&n);
        q.push((node){1, n, n});
        while(q.size()){
            node e = q.top(); q.pop();
            if(e.val & 1) mid = (e.r + e.l) / 2;
            else mid = (e.r + e.l) / 2;
            res[mid] = ++ cnt;
            if(mid > e.l) q.push((node){e.l, mid - 1, mid - e.l});
            if(mid < e.r) q.push((node){mid + 1, e.r, e.r - mid});
        }
        for(int i = 1; i <= n; ++ i){
            printf("%d",res[i]);
            if(i == n) printf("
");
            else printf(" ");
        }
    }
    return 0;
}

E. K-periodic Garland

题意： 给一个01串，求最少修改多少个字符使得两个 1 之间有 (k-1) 个 0。

题解：

用 (dp[i][0]) 表示使第 i 位为 0 且前 i 位满足要求的最少修改次数。同样 (dp[i][1]) 表示使第 i 位为 1 且前 i 位满足要求得最少修改次数。

状态转移：

[egin{aligned} dp[i][0] &= min(dp[i-1][0],dp[i-1][1]) + (s[i] e 0) \ \ dp[i][1] &= min left{egin{array}{l} min lbrace sum[i - 1]，dp[i - k][1]+sum[i-1]-sum[i-k] brace + (s[i] e 1)&(i >= k)\ \ sum[i - 1]+(s[i] e 1)&(i < k) end{array} ight. end{aligned} ]

#include<bits/stdc++.h>
using namespace std;
#define rep(i, l, r) for(long long i = l; i <= r; ++ i);
#define per(i, r, l) for(long long i = r; i >= l; -- i);
typedef long long ll;
typedef pair<int, int> PII;
const int N = 2e6 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const ll INF = 1e18+1;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//

int T, n, k, res;   
int dp[N][2], sum[N];
char s[N];

int main()
{
    scanf("%d",&T);
    while(T --){
        scanf("%d%d", &n, &k);
        scanf("%s", s + 1);
        sum[0] = 0; dp[0][0] = dp[0][1] = 0;
        for(int i = 1; i <= n; ++ i) sum[i] = sum[i - 1] + (s[i] == '1');

        for(int i = 1; i <= n; ++ i){
            dp[i][0] = min(dp[i - 1][0], dp[i - 1][1]) + (s[i] != '0');
            if(i > k) dp[i][1] = min(sum[i - 1], dp[i - k][1] + sum[i - 1] - sum[i - k]) + (s[i] != '1');
            else dp[i][1] = sum[i - 1] + (s[i] != '1');
        }
        printf("%d
",min(dp[n][0], dp[n][1]));
    }
    return 0;
}

F. Decreasing Heights

题意： 给出一个网格图，每个格子有其高度，从((1, 1)) 出发，前往 ((n, m)) , 每次只能从格子((i, j)) 向下或向右移动到 ((i + 1, j)) 和 ((i, j + 1))。还有一个限制：每次只能从高度为 (x) 的格子移动到高度为 (x + 1) 的格子上。可以无限次地执行将一个格子高度减1的操作,问最少需要多少次操作可以从((1, 1)) 移动到 ((n, m))。

题解：

首先证明解决本题的一个关键信息：这条路径上必然有一个点高度不变。

证明先略。。

有了这个信息后，我们观察下图，其中紫色为一条((1, 1)) 到 ((n, m)) 的路径，且假设红色方格 (x, y) 为高度不变的格子，高度为k, 按照题目的限制这条路径上其他格子((i, j ))应该被修改为如下标记的高度。也就是 (k+dis) ，其中 (dis = i + j - x- y)。

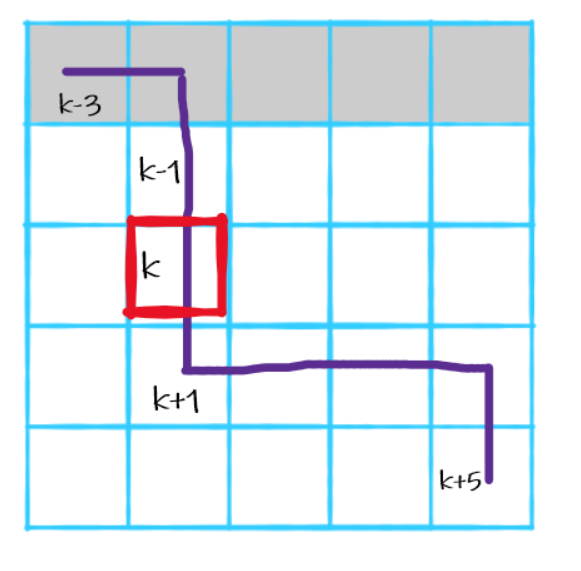
当知道某个格子高度不变后，它所在路径上其他格子应该修改为的值也确定了。那么我没可以枚举哪个格子的高度不变，然后更新dp[] []数组，其中dp[i] [j]表示从 ((1, 1)) 到 ((i, j)) 的最少修改次数。这个是个很常见的模型。

[a[i][j] >= (a[x][y] + dis) 时 \ dp[i][j]=min lbrace dp[i-1][j],dp[i][j-1] brace +a[i][j]-(a[x][y]+dis) ]

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
typedef pair<int,int>PII;
const int N = 1e5 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const ll INF = 1e18;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//

int T, n, m;
ll dp[105][105], a[105][105];

int main()
{
    scanf("%d",&T);
    while(T --){
        scanf("%d%d",&n,&m);
        for(int i = 1; i <= n; ++ i){
            for(int j = 1; j <= m; ++ j)
                scanf("%lld",&a[i][j]);
        }
        ll res = INF;
        for(int x = 1; x <= n; ++ x){
            for(int y = 1; y <= m; ++ y){
                
                for(int i = 0; i <= n; ++ i)
                    for(int j = 0; j <= m; ++ j)
                        dp[i][j] = INF;
                dp[1][0] = 0;
                
                for(int i = 1; i <= n; ++ i){
                    for(int j = 1; j <= m; ++ j){
                        ll dis = i + j - x - y;
                        if(a[i][j] < a[x][y] + dis) continue;
                        dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + a[i][j] - (a[x][y] + dis);
                    }
                }
                res = min(res, dp[n][m]);
            }
        }
        printf("%lld
",res);
    }
    return 0;
}