Topic:关于多项式正则化问题
Description:对历届奥运会男子自由泳100米取胜时间数据进行拟合
Environment:Win 10 + matlab 2015
Date: 2018.10.18-19 by hw_Chen
(需要程序和数据集的朋友可以私聊Q:1621673079,并备注:CSDN + 程序)
1.不对数据做预处理
先观察数据集分布,大约在1895年时,出现了一个离群点(由于其他数据点均满足一定的线性关系,并且大致在直线附近,如图1),同时数据集中存在部分数据的缺失,如1890年等。为了尽可能多的拟合数据点(当然这样极可能造成很大的过拟合),暂时不对数据点做任何预处理,包括不进行舍弃离群点和对样本缺失值的补充。选择六次多项式归(虽然这并不是很符合实际,但在这里主要以多尝试不同阶次为主,作为平常练习)来对样本点进行拟合,图1由程序LineRegression.m画出,图2是采用多项式回归,分别是一元线性回归、二次多项式回归、三次多项式回归、六次多项式回归,图3是分别采用标准六次多项式回归和正则六次多项式。其中红色线为标准多项式回归,蓝色线为标准多项式回归。
观察图2曲线,由程序PloynomialRegression.m画出。各多项式曲线与一元线性回归曲线相比,在训练集上效果相仿,但在测试集上,一元线性回归的效果明显比多项式回归好,说明在不对数据做任何预处理的情况下,一元线性回归学习到了训练集的数据的内在规律,而不是仅仅追求对数据点的尽可能的拟合,其对未知样本的泛化能力更好,显然多项式回归在本例中产生了过拟合。**我们提出假想1:数据本质是一元线性关系,加入多项式后,高次项增加了模型的过拟合。**事实上,抛开误差较大的数据点,其余数据点是满足线性关系的,又因为变量只有参会时间,故满足一元线性关系的。
观察图3曲线和训练及测试损失,正则化的效果都比未正则化的好,虽然正则化后训练损失增加了,但测试损失减小了,说明对未知样本的泛化能力更好,能够更准确地预测未知样本。实验中为了方便观察损失变化,图3曲线暂时设置lambda=3000,由程序RegularizedPloynomialRegression.m画出。 (实验中采用误差平方和计算公式作为损失计算方法)
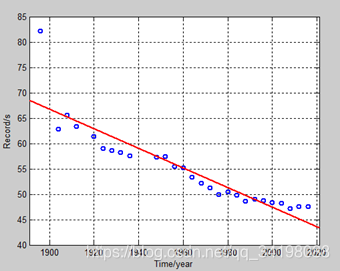
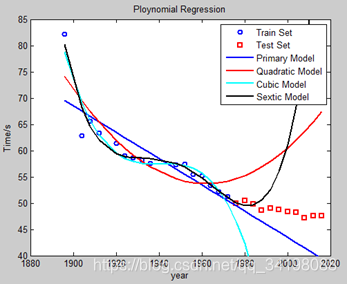
图1 一元线性回归 图2 多项式回归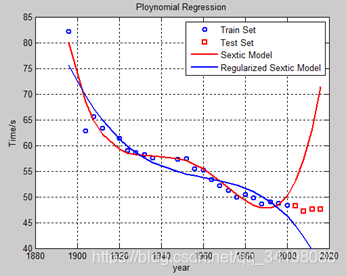
图3 标准六次多项式回归和正则六次多项式回归

再来看看图3两种情况下求解的参数theta的情况:
标准多项式回归参数theta3:
正则多项式回归参数theta4:
从上到下依次是一次项、二次项、…、六次项的系数。可以看出正则化后各高次项除五次项外系数都减小了。正则化后的测试损失更小了,我们修改下假想1,提出假想2:加入多项式,高次项增加了过拟合,但正则化后,正则项使多项式系数趋于0,减弱高次项的影响以达到减小损失的目标。
先看看损失计算函数:
标准多项式回归损失函数计算公式:
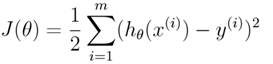 (式1)
(式1)
正则化多项式回归损失函数计算公式:
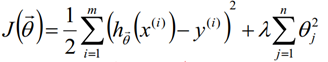 (式2)
(式2)
理论分析下,首先假设使用式1计算得到标准多项式回归的损失为a,则使用式2计算正则化多项式回归的损失为a+b,其中a、b均大于0 。在利用梯度下降法求解参数theta的情况下,损失对theta求偏导再乘以学习率alpha即得惩罚,在每一步迭代中,显然正则多项式对于误差的惩罚更大,故能够更最后使得损失会更小。虽然在这里,正则化后训练损失增大了,那是因为曲线并非完全追求拟合全部的数据点,而是更加注重学习数据内在规律,并且为了使正则化效果看起来更好,此处的lambda也并非最佳取值,在下文中会提到在这个数据集中最佳lambda取值。
梯度下降法迭代公式:
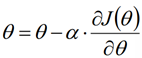 (式3)
(式3)
利用迭代次数作为梯度下降法的终止条件,值得注意的是,使用梯度下降法时,如果各输入数据间差距太大时,需要对数据进行规范化,否则梯度下降法下降缓慢,甚至发散。
首先让我们先看看,当把迭代次数设置成10次时(为什么迭代次数一开始就设置成10呢?后面会提到,因为随着次数的增加,各个图的区别越不明显)。其中横坐标是迭代次数,纵坐标是参数的变化。theta1是标准六次多项式参数,theta2是正则化六次多项式参数。theta1(1)、theta1(2)、theta1(3)、…、theta1(7)分别是标准六次多项式常数项、一次项、二次项、…、六次项系数,同样theta2(1)、theta2(2)、theta2(3)、…、theta2(7) 分别是正则六次多项式常数项、一次项、二次项、…、六次项系数,程序由ModifiedRPR.m画出。先上图~~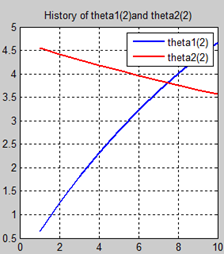
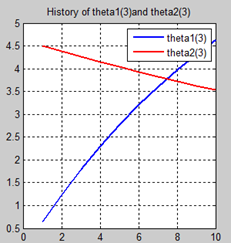
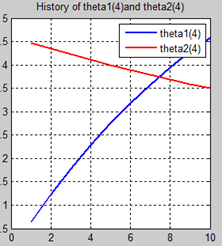
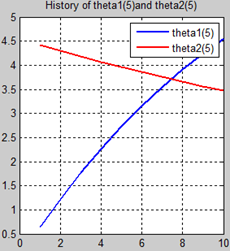
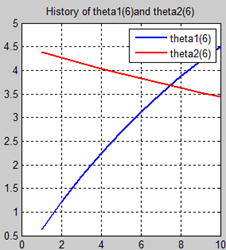
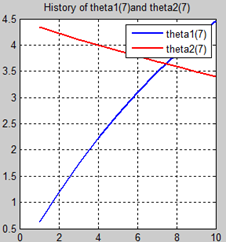
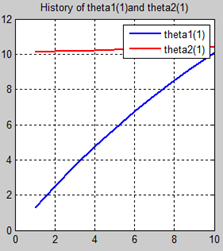
观察这些图,除第一幅图外,即常数项系数图,其他六幅图基本趋势和形状相同,为了确保所画图的真实性,先看theta1和theta2的历史数据。
theta1历史数据: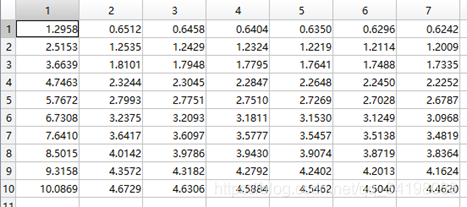
theta2历史数据: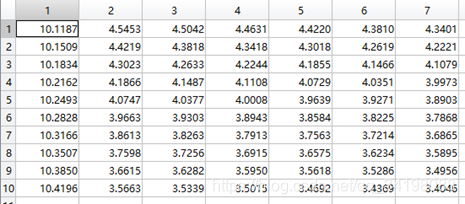
观察这些数据,以theta1数据为例,每列从上到下看,2-7列变化趋势且取值相仿,同样theta2数据同样有这样的规律,说明所画的图是正确的。
迭代次数n=10时,它整体长这样:
n=20: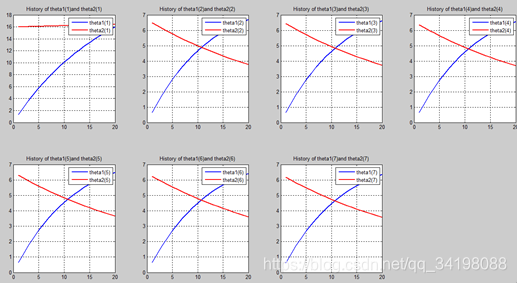
n=30: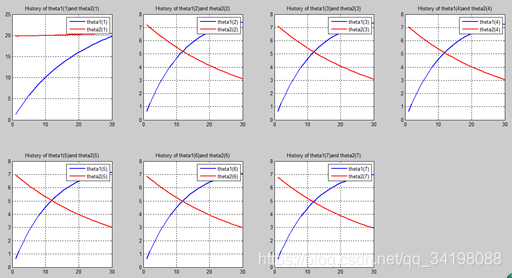
n=60: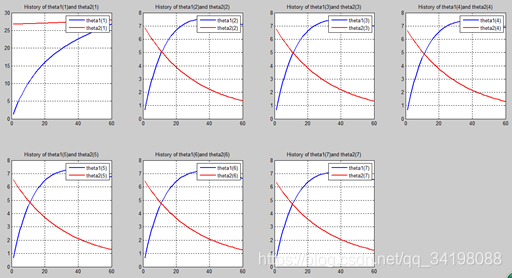
n=100: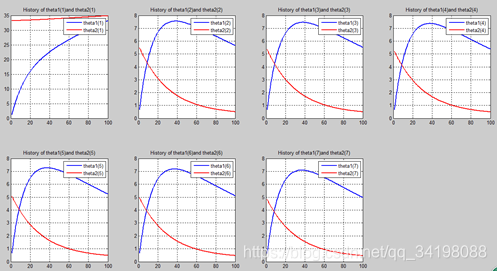
n=200: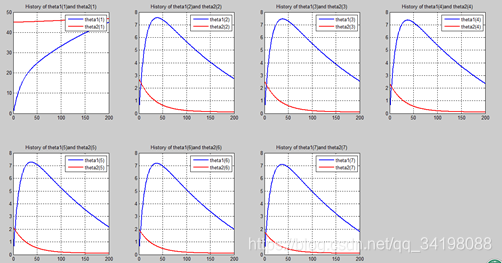
n=1000: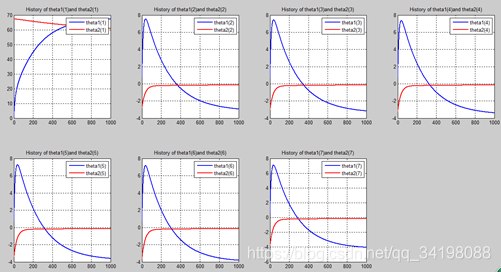
n=2000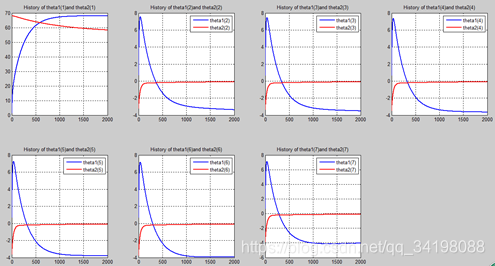
N=5000: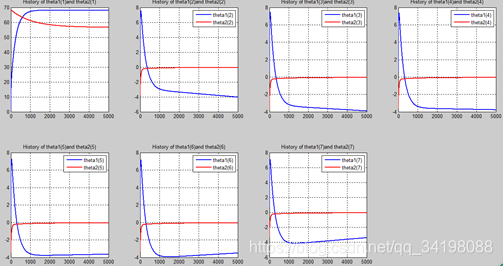
n=10000: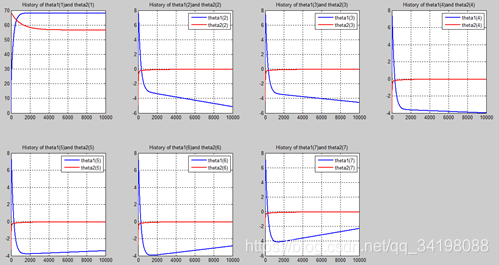
从上图中可以看出(稍微有点多),正如假想2中那样,正则项的加入能够使高次项的影响减弱,一次项及高次项系数皆趋近于0,至于为什么拟合的曲线不是一条直线,是因为即使其系数趋于0,但并没有等于0,对于曲线的构成还有影响。综上假想2是正确的。
不同的lambda值对曲线的拟合与预测也有不同的影响,下面是不同lambda对应的训练损失和测试损失。由ModifiedRPR_Lambda.m得出: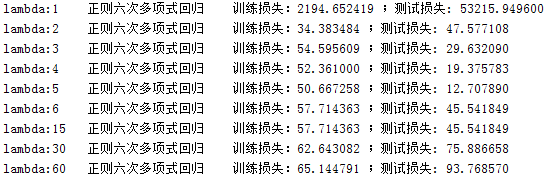
可以看出lambda=5时,是最佳的取值,其对应的多项式拟合曲线如下图: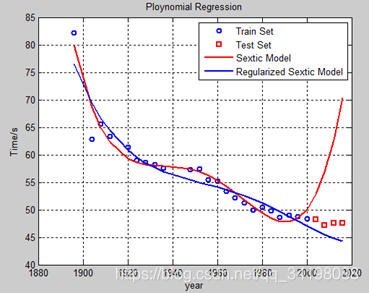
2.对数据进行预处理
观察本实验所用的数据集,发现有离群的噪声点和数据缺失,如果不进行数据预处理,会影响模型的效果。博客【1】中介绍的介绍了一些异常数据处理的方法,在本次实验,采用舍弃噪声较大的离群点和相邻两值取平均的插值方法,因为在缺失的1916年和1940及1944年附近数值变化较缓慢,因此采用取平均的插值方法是可行的。下图是未进行数据处理和进行数据处理的对比图,由程序ModifiedRPR2.m得出。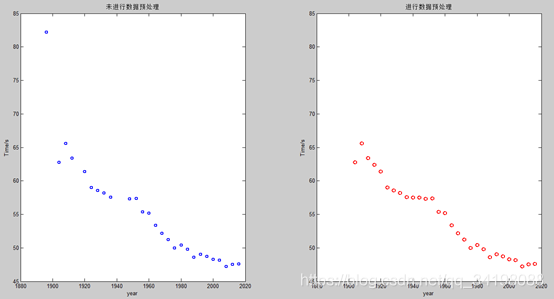
再分别对上述两组数据集作标准六次多项式回归和正则六次多项式回归。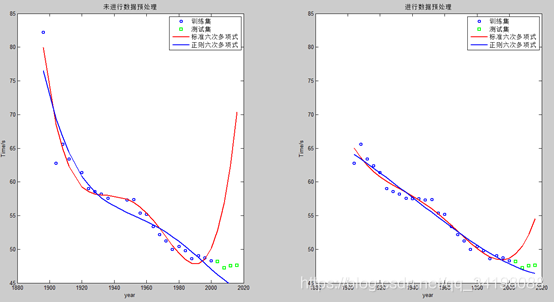
左侧图正则六次多项式回归最佳lambda=5,右侧最佳lambda=15。两两对比发现,进行数据预处理后的无论是正则化模型还是标准模型对未知样本的预测能力都更好,拥有更好的泛化能力。尤其是正则化后,训练损失变为原来的约1/5,测试损失约原来的1/12,因此说明数据预处理的重要性。数据预处理后的正则化曲线近似一条直线,但又带有一定曲线特征,这再次印证了上面提到的“正则化减小高次项系数的绝对值,以达到减弱高次项影响的效果”。
【1】https://blog.csdn.net/ge341204/article/details/80720369
【2】袁梅宇.机器学习基础-原理、算法与实践[M].北京:清华大学出版社,2018