如何打印矩阵

如何打印矩阵

顺时针方向打印矩阵

如何顺时针打印一个矩阵的元素呢，例如：如果输入如下矩阵：

1              2              3              4
5              6              7              8
9              10           11           12
13           14           15           16

则依次打印出数字：1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10。

思路：用类似深度搜索的方法来做，每次朝一个方向走，如果不能再走了顺时针转向。

int array[1000][1000];
int canUse[1000][1000];
int step[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

void Scan(int x, int y, int direct, int m, int n)
{
    int i;
    canUse[x][y] = 0;
    printf("%d ", array[x][y]);

    for (i = 0; i < 4; i++) {
        int j = (direct + i) % 4;
        int tx = x + step[j][0];
        int ty = y + step[j][1];

        if (0 <= tx && tx < m && 0 <= ty && ty < n && canUse[tx][ty]) {
            Scan(tx, ty, j, m, n); 
        }   
    }   
}

int main()
{
    int m = 4, n = 4;
    int i, j, v=1;

    for (i=0; i<m; i++) {
        for (j=0; j<n; j++) {
            array[i][j] = v++;
            canUse[i][j] = 1;
        }   
    }   

    Scan(0, 0, 0, m, n); 
    printf("
");
}

---

沿对角线方向迂回遍历矩阵

如何沿对角线方向迂回遍历一个矩阵的元素呢，例如：如果输入如下矩阵：

1              2              3              4
5              6              7              8
9              10           11           12
13           14           15           16

则依次打印出数字：1, 2, 5, 9, 6, 3, 4, 7, 10, 13, 14, 11, 8, 12, 15, 16

思路：同一连线上的点，其坐标x+y必然都相等

偶数次（从0开始计数）沿右上方向运动；奇数次则沿左下方向运动。

int main()
{
    int M = 4, N = 4;
    int matrix[M][N];
    int i, j, v=1;

    for (i=0; i<M; i++) {
        for (j=0; j<N; j++) {
            matrix[i][j] = v++;
        }   
    }   

    for (i = 0; i < M + N; i++) {
        if (i % 2 == 0) {
            int j = i < M ? i : M - 1;
            int k = i - j;

            while (j >= 0 && k < N) {
                printf("%d, ", matrix[j--][k++]);
            }   

        } else {
            int k = i < N? i : N -1; 
            int j = i - k;
            while(k >= 0 && j < M){ 
                printf("%d, ", matrix[j++][k--]);
            }   
        }   

    }   

    printf("
");
}

---

打印螺旋矩阵

下面是一个螺旋队列： 

   73   74   75   76   77   78   79   80  81
   72   43   44   45   46   47   48   49   50
   71   42   21   22   23   24   25   26   51
   70   41   20    7     8      9   10   27   52
   69   40   19    6     1     2    11   28   53
   68   39   18    5     4     3    12   29   54
   67   38   17   16   15   14   13   30   55
   66   37   36   35   34   33   32   31   56
   65   64   63   62   61   60   59   58   57

看清以上数字排列的规律，设1点的坐标是(0,0)，x方向向右为正，y方向向下为正。例如：7的坐标为(-1,-1)，2的坐标为(1,0)，3的坐标为(1,1)。编程实现输入任意一点坐标(x,y)，输出所对应的数字；或输入任意数字，输出该数字的坐标。
解析：规律能看出来，问题就在于如何利用它。很明显这个队列是顺时针螺旋向外扩展的，我们可以把它看成一层一层往外延伸。第 0 层规定为中间的那个 1，第 1 层为 2 到 9，第 2 层为 10 到 25，注意到 1、9、25、……不就是平方数吗？而且是连续奇数（1、3、5、……）的平方数。这些数还跟层数相关，推算一下就可以知道第 t 层之内一共有 (2t-1)^2 个数，因而第 t 层会从 [(2t-1)^2] + 1 开始继续往外螺旋。给定坐标 (x,y)，如何知道该点处于第几层？层数 t = max(|x|,|y|)。
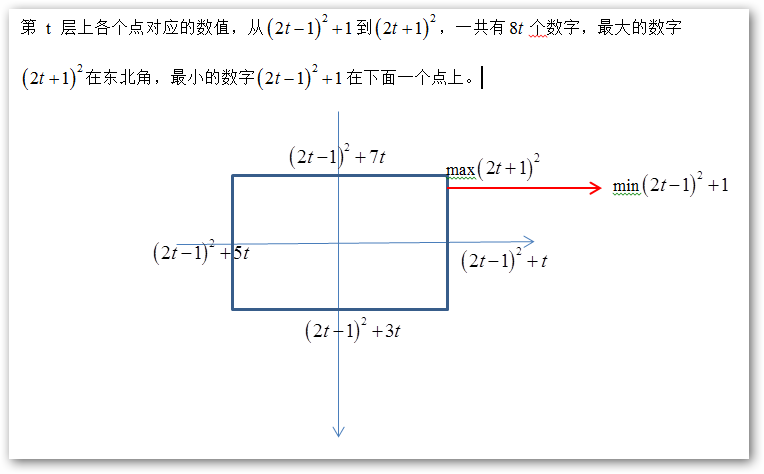
　　知道了层数，接下来就好办多了，这时我们就知道所求的那点一定在第 t 层这个圈上，顺着往下数就是了。要注意的就是螺旋队列数值增长方向和坐标轴正方向并不一定相同。我们可以分成四种情况——上、下、左、右——或者——东、南、西、北，分别处于四条边上来分析。
　　东|右：x == t，队列增长方向和 y 轴一致，正东方向（y = 0）数值为 (2t-1)^2 + t，所以 v = (2t-1)^2 + t + y
　　南|下：y == t，队列增长方向和 x 轴相反，正南方向（x ＝ 0）数值为 (2t-1)^2 + 3t，所以 v ＝ (2t-1)^2 + 3t - x
　　西|左：x == -t，队列增长方向和 y 轴相反，正西方向（y ＝ 0）数值为 (2t-1)^2 + 5t，所以 v = (2t-1)^2 + 5t - y
　　北|上：y == -t，队列增长方向和 x 轴一致，正北方向（x ＝ 0）数值为 (2t-1)^2 + 7t，所以 v ＝ (2t-1)^2 + 7t + x
　　其实还有一点很重要，不然会有问题。其它三条边都还好，但是在东边（右边）那条线上，队列增加不完全符合公式！注意到东北角（右上角）是本层的最后一个数，再往下却是本层的第一个数，那当然不满足东线公式啊。所以我们把东线的判断放在最后（其实只需要放在北线之后就可以），这样一来，东北角那点始终会被认为是北线上的点。

下面给出第 t 层的图示说明：

//螺旋队列问题  
  
#include <iostream>  
using namespace std;  
  
#define max(a,b) ((a)>(b) ? (a) : (b))  
#define abs(a) ((a)>0 ? (a) : -(a))  
#define square(a) ((a)*(a))  
  
//输入坐标，输出对应的数字  
int Spiral_Queue(int x, int y){  
    int val;                    //该坐标对应的数值  
    int t = max(abs(x),abs(y)); //该坐标所在的层数  
    if(y == -t)                 //北边（北边的判断分支要先于东边，这是为了东北角最大值考虑的）  
        val = square(2*t-1)+7*t+x;  
    else if(y == t)             //南边  
        val = square(2*t-1)+3*t-x;  
    else if(x == -t)            //西边  
        val = square(2*t-1)+5*t-y;  
    else if(x == t)             //东边  
        val = square(2*t-1)+t+y;  
    return val;  
}  
  
  
int main(){  
    int x,y;  
    const int N = 4;        //需要打印的层数  
    for(y=-N; y<=N; y++){  
        for(x=-N; x<=N; x++)  
            cout<<Spiral_Queue(x,y)<<"  ";  
        cout<<endl;           //按y层打印，换行  
    }  
    return 0;  
}