尾调用

尾调用

本文将以lua语言来描述。

尾调用是函数式编程的一个概念，它是指某个函数的最后一步是调用另一个函数，例如：

function f(x)
    return g(x)   -- 尾调用
end

尾调用不一定出现在函数尾部，只要是最后一步操作即可，例如：

function f(x) 
    if (x > 0) then
        return m(x)
    end

    return n(x);
end

上面代码中，函数m和n都属于尾调用，因为它们都是函数f 的最后一步操作。

但以下情况均不属于尾调用：

function f(x)
    return g(x)+1   　　　　 -- must do the addition
end

function f(x)
    return x or g(x)    　　-- must adjust to 1 result
end

function f(x)
    ret = g(x)
    return ret
end

我们知道，函数调用会在内存形成一个调用栈（call stack），调用函数（caller）与被调函数（callee）的关系如下图：

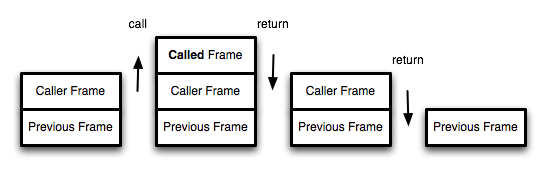
可见，被调函数有一个压栈和出栈的过程。

而尾调用由于是函数的最后一步操作，所以不需要保留外层函数的调用记录，因为调用位置、内部变量等信息都不会再用到了，只要直接用内层函数的调用记录，取代外层函数的调用记录就可以了。

如下里面的例子：

function g(x, y)
    return x + y 
end

function f() 
  m = 1;
  n = 2;
  return g(m, n); 
end

f()

上面代码中，如果函数g不是尾调用，函数f就需要保存内部变量m和n的值、g的调用位置等信息。

但由于调用g之后，函数f就结束了，所以执行到最后一步，完全可以删除 f() 的调用记录，只保留 g() 的调用记录，这就叫做"尾调用优化"（Tail call optimization），即只保留内层函数的调用记录。如果所有函数都是尾调用，那么完全可以做到每次执行时，不使用额外的调用栈空间，这将大大节省内存。这就是"尾调用优化"的意义。

利用这个特性在处理尾调用时不使用额外的栈，那么尾调用递归的层次是可以无限制的。

例如：

function factorial(n) 
  if n == 1 then return 1 end
  return n * factorial(n - 1);
end

print(factorial(5)) -- 120

上面代码是一个阶乘函数，计算n的阶乘，最多需要保存n个调用记录，空间复杂度 O(n) 。

如果改写成尾递归，只保留一个调用记录，复杂度 O(1) 

function factorial(n, total)
    if n == 1 then return total end
    return factorial(n - 1, n * total);
end

print(factorial(5, 1)) -- 120

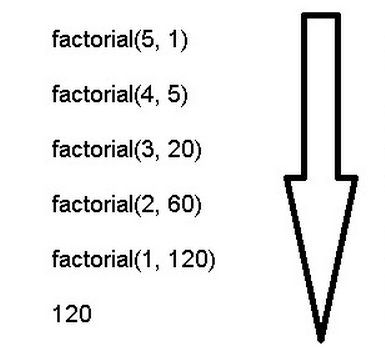
由此可见，"尾调用优化"对递归操作意义重大，所以一些函数式编程语言将其写入了语言规格。ES6也是如此，第一次明确规定，所有 ECMAScript 的实现，都必须部署"尾调用优化"。这就是说，在 ES6 中，只要使用尾递归，就不会发生栈溢出，相对节省内存。

尾递归的实现，往往需要改写递归函数，确保最后一步只调用自身。做到这一点的方法，就是把所有用到的内部变量改写成函数的参数。比如上面的例子，阶乘函数 factorial 需要用到一个中间变量 total ，那就把这个中间变量改写成函数的参数。这样做的缺点就是不太直观，第一眼很难看出来，为什么计算5的阶乘，需要传入两个参数5和1？

解决这个问题的方法一是在尾递归函数之外，再提供一个正常形式的函数。

function tailfactorial(n, total)
    if n == 1 then return total end
    return tailfactorial(n - 1, n * total);
end

function factorial(n)   
    return tailfactorial(n, 1)
end

print(factorial(5)) -- 120

上面代码通过一个正常形式的阶乘函数 factorial ，调用尾递归函数 tailFactorial ，看起来就正常多了。