常见的方法有：选取更好的代价函数，就是被称为交叉熵代价函数（the cross-entropy cost function）；
四种正则化方法（L1和L2正则、dropout、训练数据的扩展）
一.交叉熵代价函数：
考虑一下神经元的学习方式：通过计算代价函数的偏导 和
来改变权重和偏移。那么我们说「学习速度很慢」其实上是在说偏导很小。因为SIGMOD激活函数的特性，在0和1附近变化缓慢。
我们可以用不同的代价函数比如交叉熵（cross-entropy）代价函数来替代二次代价函数
假设神经元的输出为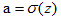
，z为加权输入（权重和+偏置b）。
定义神经元的交叉熵代价函数为：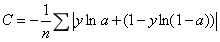
n是训练数据的个数，这个加和覆盖了所有的训练输入x，y是期望输出。
交叉熵有两个特性能够合理地解释为何它能作为代价函数。首先，它是非负的。因为等式加和里的每一项都是负的，它们的对数是负的；整个式子的前面有一个负号。
其次，如果对于所有的训练输入 ，这个神经元的实际输出值都能很接近我们期待的输出的话，那么交叉熵将会非常接近0。
事实上，我们的均方代价函数也同时满足这两个特征。
交叉熵有另一个均方代价函数不具备的特征，它能够避免学习速率降低的情况。
因为交叉熵对权重的偏导为：
上式告诉我们权重的学习速率可以被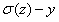
控制，，也就是被输出结果的误差所控制，那么误差越大我们的神经元学习速率越大。
此外它还能避免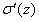
导致的学习减速。因为交叉熵中的该项被抵消掉了，不必担心它会变小。
交叉熵对偏移的偏导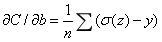
与对权重的偏导形式相似也避免了学习速率低的问题。
二. Softmax
Softmax的主要思想是为神经网络定义一种新的输出层，它也是对加权输入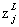
进行计算，只是在获取输出结果的时候我们不使用SIGMOD函数，使用softmax函数代替。第j个输出神经元的激活值为：
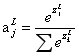
分母对所有的输出神经元k求和。
使用softmax时，所有的输出激活值加起来必须为1，因为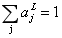
于是某个输出激活值增大或减小时，其余的输出激活值则会相应的减小或增大以维持平衡。
从softmax 层得到的输出是一系列相加和为1的正数。换言之，从softmax 层得到的输出可以看做是一个概率分布。于是可以将输出激活值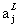
看作是神经网络认为结果是j的概率。
但是如果使用 sigmoid 输出层，我们不能使用 softmax 的结论去解读。
三． 过拟合和正则化
我们使用validation_data而不是test_data来预防过拟合。为了做到这一点，在每一步训练之后，计算validation_data的分类精度。一旦validation_data的分类精度达到饱和，就停止训练。这种策略叫做提前终止（early stopping）。当然在实践中，我们并不能立即知道什么时候准确度已经饱和。取而代之，我们在确信精度已经饱和之前会一直训练。
通过validation_data来选择不同的超参数（例如，训练步数、学习率、最佳网络结构、等等）是一个普遍的策略。我们通过这样的评估来计算和设置合适的超参数值。如果基于test_data的评估结果设置超参数，有可能我们的网络最后是对test_data过拟合。也就是说，我们或许只是找到了适合test_data具体特征的超参数，网络的性能不能推广到其它的数据集。
由于validation_data 和test_data 是完全分离开的，所以这种找到优秀超参数的方法被称为分离法（hold out method）。
一般来说，增加训练数据的数量是降低过拟合的最好方法之一。
另一种避免过拟合的方法是减小网络的规模。然而，我们并不情愿减小规模，因为大型网络比小型网络有更大的潜力。
正则化也可以避免过拟合，一种最常用的正则化技术——权重衰减（weight decay）或叫L2正则（L2 regularization）。L2正则的思想是，在代价函数中加
入一个额外的正则化项。
如：正则化后的交叉熵：
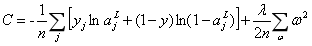
加入了第二项，也就是网络中所有权值的平方和。它由参数
进行调整，其中
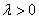被称为正则化参数（regularization parameter）。注意正则化项不包括偏移。
正则化的作用是让网络偏好学习更小的权值，而在其它的方面保持不变。选择较大的权值只有一种情况，那就是它们能显著地改进代价函数的第一部分。换句话说，正则化可以视作一种能够折中考虑小权值和最小化原来代价函数的方法。
当
较小时，我们偏好最小化原本的代价函数，而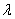
较大时我们偏好更小的权值。
使用L2正则化后，权值的学习规则变为：
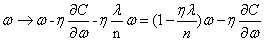
即我们以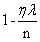
调整权值，也称权重衰减。
经验表明，当在多次运行我们的MNIST网络，并使用不同的（随机）权值初始化时，发现未正则化的那些偶尔会被「卡住」，似乎陷入了代价函数的局部最优中。结果就是每次运行可能产生相当不同的结果。相反，正则化的那些每次运行可以提供更容易复现的结果。
小权重意味着网络的行为不会因为我们随意更改了一些输入而改变太多。这使得它不容易学习到数据中局部噪声。可以把它想象成一种能使孤立的数据不会过多影响网络输出的方法，相反地，一个正则化的网络会学习去响应一些经常出现在整个训练集中的实例。
与之相对的是，如果输入有一些小的变化，一个拥有大权重的网络会大幅改变其行为来响应变化。因此一个未正则化的网络可以利用大权重来学习得到训练集中包含了大量噪声信息的复杂模型。
允许大规模的偏置使我们的网络在性能上更为灵活——特别是较大的偏置使得神经元更容易饱和，这通常是我们期望的。由于这些原因，我们通常不对偏置做正则化。