Finite Sums and Sigma Notation
Sigma notation enables us to write a sum with many terms in the compact form
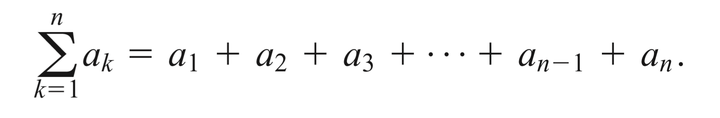
The Greek letter (capital sigma, corresponding to our letter S), stands for “sum.” The index of summation k tells us where the sum begins (at the number below the symbol) and where it ends (at the number above ). Any letter can be used to denote the index, but the letters i, j, and k are customary.
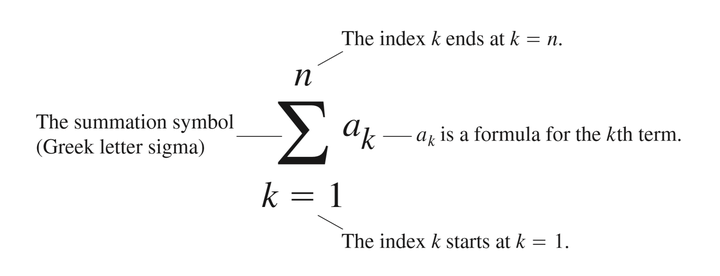
Thus we can write

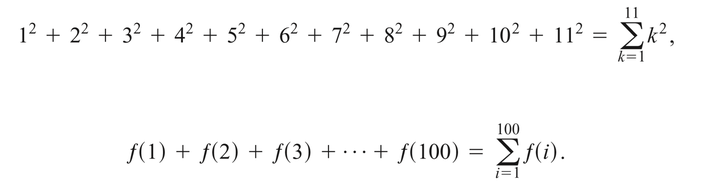
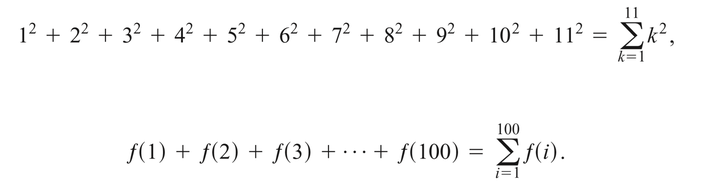
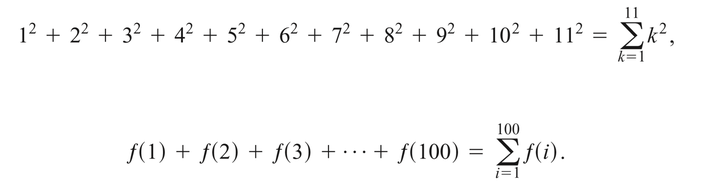
The sigma notation used on the right side of these equations is much more compact than the summation expressions on the left side.

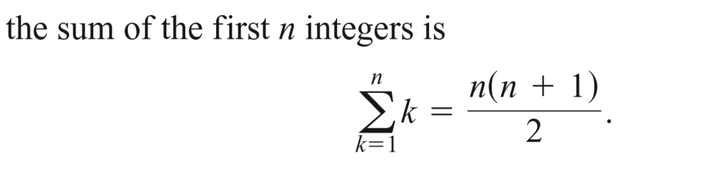
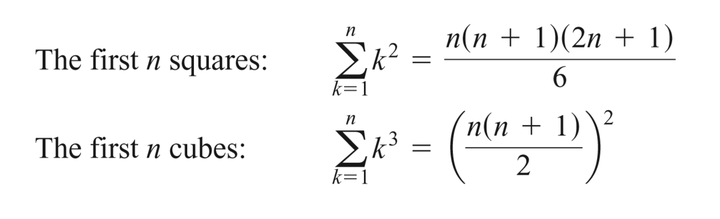
Notation and Existence of the Definite Integral
The symbol for the number I in the definition of the definite integral is
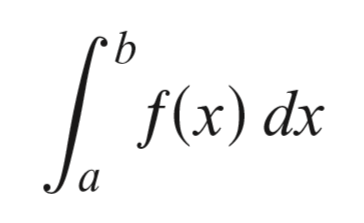
which is read as “the integral from a to b of ƒ of x dee x” or sometimes as “the integral from a to b of ƒ of x with respect to x.” The component parts in the integral symbol also have names:





