原创
问题描述:
问题描述:
给定N个物品,每个物品有一个重量W和一个价值V.你有一个能装M重量的背包.问怎么装使得所装价值最大.每个物品只有一个.
输入格式
输入的第一行包含两个整数n, m,分别表示物品的个数和背包能装重量。
以后N行每行两个数Wi和Vi,表示物品的重量和价值
以后N行每行两个数Wi和Vi,表示物品的重量和价值
输出格式
输出1行,包含一个整数,表示最大价值。
样例输入
3 5
2 3
3 5
4 7
2 3
3 5
4 7
样例输出
8
数据规模和约定
1<=N<=200,M<=5000.
解题思路:
大家应该都看过很多大神的代码了,如果还有不明白的地方,不妨听听我的解释,希望能给你带来柳暗花明的感觉。
首先大家都应该知道,一个物品,有放与不放两种选择,我们的最终结果就是综合所有物品放与不放的选择来确定。
有这样一个状态方程:
F[ i ][ j ]=max( F[ i-1 ][ j ] ,F[ i-1 ][ j - wi[i] ] + vi[ i ] );
其实不难理解,F[ i ][ j ] 代表 当放到第 i 个物品时,此时容量还剩 j ,我们可以选择放或者不放;
不放的话 F[ i ][ j ]=F[ i-1 ][ j ];就是相当于放了前 i-1 个物品中的物品;注意,不一定是前 i-1 个
物品全都放进了背包。第 i 个物品放进去的话 F[ i ][ j ]=F[ i-1 ][ j - wi[i] ] + vi[ i ]; 放进去了所以
在前面放了 i-1 个物品中的物品的基础上,容量减去 wi[i], 价值加上vi[ i ](但得在wi[i] <= j 条件下);
有些同学估计挺纳闷,在放得下的前提下从(F[ i-1 ][ j ] ,F[ i-1 ][ j - wi[i] ] + vi[ i ] ) 这两个中选择
最大的,那肯定是加入了第 i 个物品的大呀,这还需要思考吗?请看下图:
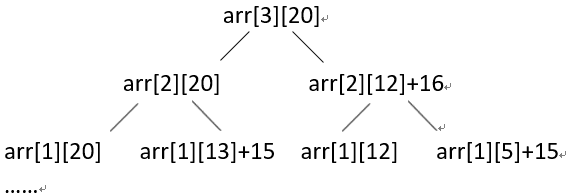
假设有3个物品,重量分别为:9、7、8;价值分别是:10、15、16,背包容量是20.
其实只要我们按照那个公式套进去,就会发现,每个物品放与不放的情况都会被遍历到,
回到上面的问题,F[ i-1 ][ j ] < F[ i-1 ][ j - wi[i] ] + vi[ i ] 是不错,但是你放了第 i 个物品,假设是这个例子
的最后一个物品,前面你或许就得少放一个物品了。也许你放了第 i 个物品,放不下 i+1 个物品了,但是 vi[ i+1 ] > vi[ i ]
所以每种情况我们都要遍历过,选出最优的。
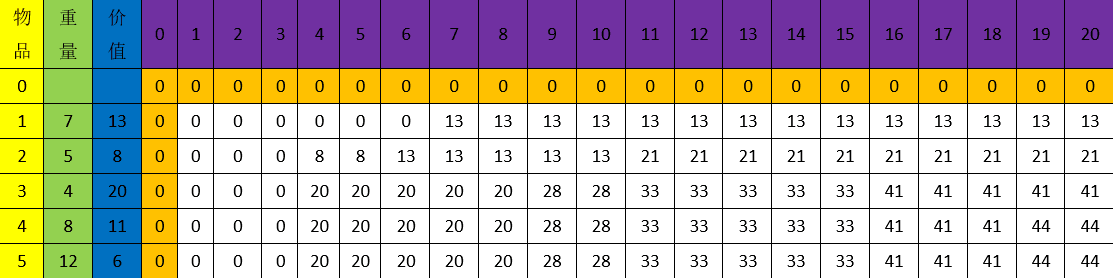
大家请看上图,思路就是从左上角开始,一行一行的求出所有放与不放的可能,右下角的44就是我们要求的答案了;但是需要注意的是,
其实很多数据我们根本用不着,从最后一行往上数,我们要的数据个数只是1、2、4、8、16个而已。
代码:

1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 5 int max(int a,int b) 6 { 7 return a>b?a:b; 8 } 9 10 int main() 11 { 12 int n,m; 13 scanf("%d%d",&n,&m); 14 15 int *w,*v; 16 w=(int *)malloc(sizeof(int)*n); 17 v=(int *)malloc(sizeof(int)*n); 18 19 int **arr; //动态分配二维数组 20 arr=(int **)malloc(sizeof(int *)*(n+1)); 21 int i; 22 for(i=0;i<=n;i++) 23 arr[i]=(int *)malloc(sizeof(int)*(m+1)); 24 25 int j; 26 for(i=0;i<=n-1;i++) 27 scanf("%d%d",&w[i],&v[i]); 28 for(i=0;i<=n;i++) 29 for(j=0;j<=m;j++) 30 { 31 if(i==0 || j==0) //0容量或者0物品置0 32 arr[i][j]=0; 33 else if(w[i-1]<=j) 34 arr[i][j]=max(arr[i-1][j],arr[i-1][j-w[i-1]]+v[i-1]); 35 else 36 arr[i][j]=arr[i-1][j]; 37 } 38 printf("%d",arr[n][m]); 39 free(arr); 40 free(w); 41 free(v); 42 return 0; 43 }
思路提升:
从上面的表格可以看到,我们用了一个二维数组存储了每一行的数据,但是实际情况是第1行数据只是第2行用,用完以后就没用了,
第 i 行的数据只是第 i+1 行使用,用完了就放在数组里面占用大量空间了;所以我们完全可以用一个 “滚动数组” 来实现这种操作,
所谓的滚动数组其实很简单,就是数组里面我们先存放第 1 行的数据,然后我们根据第 1 行的数据求出第 2 行的数据存放在数组;
就是第 i 行的数据先存放,我求出第 i+1 行的数据以后数组我来占用,这样不断变化的数组就是滚动数组,很简单吧。
代码实现:

1 #include<stdio.h> 2 #include<stdlib.h> 3 4 int max(int a,int b) 5 { 6 return a>b?a:b; 7 } 8 9 int main() 10 { 11 int n,m; 12 scanf("%d%d",&n,&m); 13 14 int *wi,*vi; 15 wi=(int *)malloc(sizeof(int)*(n+1)); 16 vi=(int *)malloc(sizeof(int)*(n+1)); 17 18 int i; 19 for(i=1;i<=n;i++) 20 scanf("%d%d",&wi[i],&vi[i]); 21 22 int *dp; 23 dp=(int *)malloc(sizeof(int)*(m+1)); //滚动数组 24 for(i=0;i<=m;i++) 25 dp[i]=0; 26 27 int j; 28 for(i=0;i<=n;i++) 29 for(j=m;j>=wi[i];j--) //容量从大到小 30 { 31 if(i==0) 32 { 33 dp[j]=0; 34 continue; 35 } 36 37 dp[j]=max(dp[j],dp[j-wi[i]]+vi[i]); 38 } 39 40 printf("%d",dp[m]); 41 return 0; 42 }
代码中状态方程变为:dp[j]=max(dp[j],dp[j-wi[i]]+vi[i]);
请大家注意,dp[j]代表的是现在要求的第 i 个物品考虑放不放在容量为 j 的物品下的最优解,而括号里面的dp[j]代表的
是放 i-1 个物品中的物品时的最优解,相当于上面的F[ i-1 ][ j ],也就是说这个是前一个状态的量,而dp[j-wi[i]]+vi[i]
就是上面的F[ i-1 ][ j - wi[i] ] + vi[ i ]了。但是容量 j 的值要从大到小了,因为我们求大容量背包的价值时要用到
小容量背包的价值,所以如果从小容量开始求,等到求放下一个物品时,从小容量开始求,那么当我们求这个物品的大容量时放与不放时
上一个物品的小容量值由于被这个物品的小容量值覆盖,所以要从大容量开始求。
2018-04-06
