原创
全排列算法是非常基础的算法,写此篇博客,旨在巩固自己的知识,理清自己的思路,有错误的地方欢迎大家指出。
还是辣个栗子:
数列 1 2 3 的全排列为:
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2
排列数的计算公式为:n!
就像是给了n个空格,拿n个数填充,第1个空格有n种填充方法,第2个空格有n-1种填充方法......
看下图:
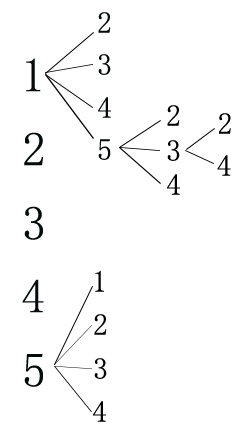
1 2 3 4 5 的全排列,第1个空格有5种填充方法,相当于第一个数和后面的5-1个数分别做了一次交换。
那么第一个空格的所有情况已经求出来了,同理,在第1个空格的基础上,第2个空格有n-1种填充方法,相当于第2个数和后面的5-2个数分别做了一次交换。
所以我们可以先把以1开头的全排列情况全部求出来,再求以2、3、4、5的,在以1开头的前提下,我们再以2开头,层层递归下去,值得注意的是,交换以后我们需要再交换回来;
不难理解为何交换回来,如果我们把1和3交换了,不交换回来的话,下一次交换就是3,4交换了,而我们是需要下一次交换1和4的。
1 #include<stdio.h>
2
3 int arr[]={1,2,3,4,5};
4
5 void swap(int a,int b) //a,b表示数组下标
6 {
7 int temp;
8 temp=arr[a];
9 arr[a]=arr[b];
10 arr[b]=temp;
11 }
12
13 void Fullsort(int n)
14 {
15 if(n==5) //输出
16 {
17 int i;
18 for(i=0;i<=4;i++)
19 printf("%d ",arr[i]);
20 printf("
");
21 return;
22 }
23
24 int i;
25 for(i=n;i<=4;i++) //第n个位置的数分别与后面4-n个位置的数(包含本身)交换
26 {
27 swap(n,i);
28 Fullsort(n+1);
29 swap(n,i); //换回来
30 }
31 }
32
33 int main()
34 {
35 Fullsort(0);
36 return 0;
37 }
12:03:33
2018-04-06