背景
继上一篇三角网格Dijkstra寻路算法之后,本篇将继续介绍一种更加智能,更具效率的寻路算法—A*算法,本文将首先介绍该算法的思想原理,再通过对比来说明二者之间的相同与不同之处,然后采用类似Dijkstra方式实现算法,算法利用了二叉堆数据结构,最后再通过一些小实验的效果展示其寻路效果。
搜索方法之启发式搜索
我们知道之所以Dijkstra算法并不高效,即使采用了好的数据结构优化,原因在于访问的节点数量太多。而A*相比于Dijkstra的优势就在于利用了更多的信息、访问更少的节点。为了方便理解A*,我们先抛开最短路径不谈,首先来介绍一下图的搜寻。我们知道在所有能被抽象为Graph的数据结构上搜索一个特定节点,我们可以采用遍历的方式。BFS(Breath-First)遍历和DFS(Depth-First)遍历,这是所有有数据结构基础的人都了解的基本图遍历方法,当然在搜索问题中,大可不必遍历所有节点,只需在遍历到终点时跳出即可。为了实现搜索节点,我们可以采用BFS和DFS这两种方式。在图G上,给定一个起点S和一个终点E,图的BFS搜索方法主要逻辑如下:
1 TravelSearch_BFS(G,S,E) 2 创建空队列容器Q 3 将S置为已访问并加入Q 4 While(Q不为空) 5 从Q中取出一个节点P 6 对P的所有邻居n 7 若n未被访问过 8 若n==E,则找到终点E,算法结束 9 将n置为已访问并加入Q 10 算法结束,未能找到终点E
DFS搜索方法(非递归式)主要逻辑如下:
1 TravelSearch_DFS(G,S,E) 2 创建空栈容器Q 3 将S置为已访问并加入Q 4 While(Q不为空) 5 从Q中取出一个节点P 6 对P的所有邻居n 7 若n未被访问过 8 若n==E,则找到终点E,算法结束 9 将n置为已访问并加入Q 10 算法结束,未能找到终点E
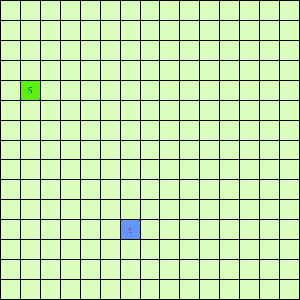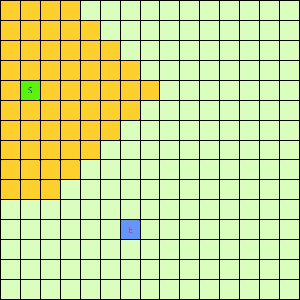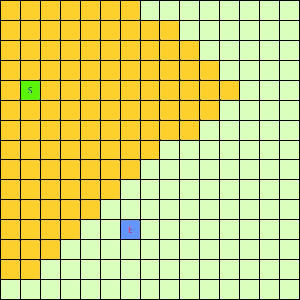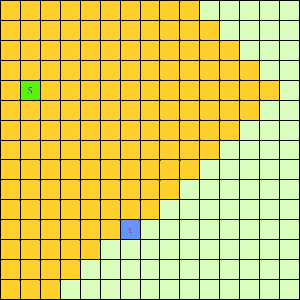
可以看出,DFS搜索和BFS搜索的关键区别在容器Q上,DFS采用LIFO的栈结构,而BFS则采用的是FIFO的队列结构。假如我们像下面这样做一个方格图,然后设置好起点和终点,规定好每个格子访问邻居的顺序为左→右→下→上的话,在这之上的DFS/BFS搜寻的演示动画已经寻路开销如下图所示:
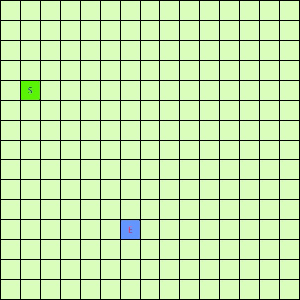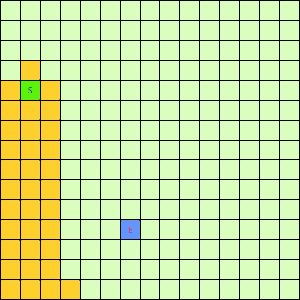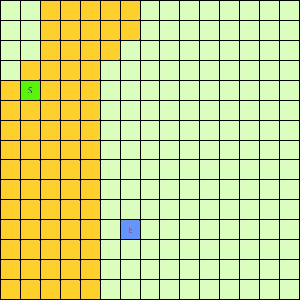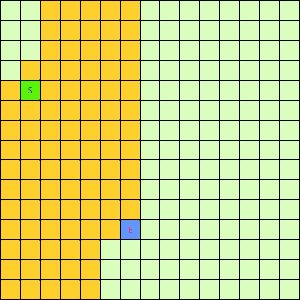 |
 |
| DFS(Depth-First)寻找终点E动画 | BFS(Breath-First)寻找终点E动画 |
可以看出仅仅是容器不一样,寻找终点访问的节点数也不一样。也就是说,容器Q的进出方式可以影响到搜寻的开销。所以我们不难想到,如果一个更加“聪明”的容器Q能够按某种优先级去弹出节点,我们就有可能更早的找到需要的节点,从而避免访问过多其他节点。事实上在方格图G上这样的一个“智能”一点的容器完全可以设计出来,只需充分利用一下方格图的特点。我们令起始方格为(1,4),终止方格为(6,10),我们根据对方格图的先验了解可以知道,起点与终点的坐标暗含了他们的位置信息,例如从S(1,4)搜寻E(6,10),显然从S出发向着“东南”方向搜寻,发现终点的可能性更大。我们根据每一个方格节点的坐标,能够求出到E的欧式距离。这样,我们完全可以设计一个与无脑的Depth-First和Breath-First不同的搜索方式,我们称其为“Best-First”。这个Best-First搜索的代码结构和BFS/DFS差不多,但关键的区别是从容器中弹出元素不再是LIFO或是FIFO方式,而是选择一个离E欧式距离更近的节点。选择离E距离更近的节点弹出的原因是我们经验上认为这样使搜索“离找到E更近了一步”。能够判断远近是方格图的特点决定的,因为不是任何无向带权图都有所谓“距离”或者“节点坐标”这样的概念。我们利用方格图的先验信息设计了这样一个Best-First智能搜寻算法。支持这个算法的容器Q我们可以设计为一个二叉堆之类的堆容器,这样可以支持高效取最值操作。这个Q每次Pop出的元素都是Q中离终点E最近的,算法逻辑可用下面的伪代码表示:
1 TravelSearch_BestFirst(G,S,E) 2 创建空堆容器Q 3 将S置为已访问并加入Q 4 While(Q不为空) 5 从Q中取出一个节点P(即P是Q中距离E最近的格子) 6 对P的所有邻居n 7 若n未被访问过 8 若n==E,则找到终点E,算法结束 9 将n置为已访问并加入Q 10 算法结束,未能找到终点E
让我们看看他的执行效果:
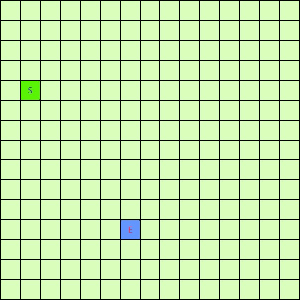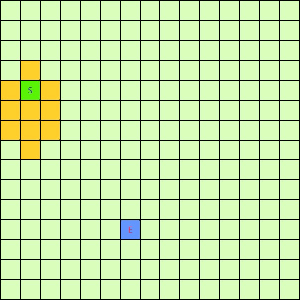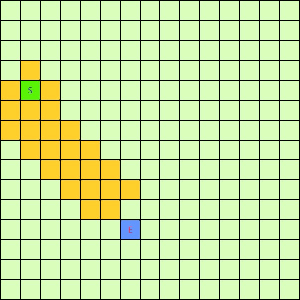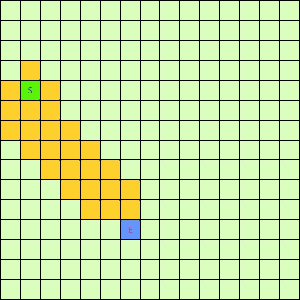
这一看我们设计的Best-First果然比DFS和BFS更直接了当,几乎是一路冲向终点,这样只遍历了很少的节点就找到终点。不过我们的方格图可没这么简单,一般来说是有点障碍物的,所以我们就设计一个有障碍物的方格图,用红叉方格表示,然后让这三种方法再去跑一遍,结果如下:
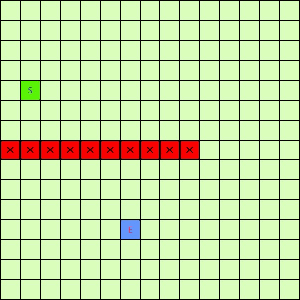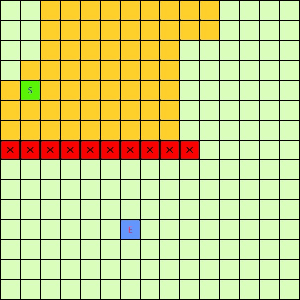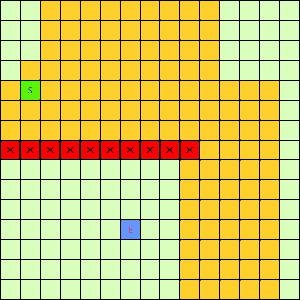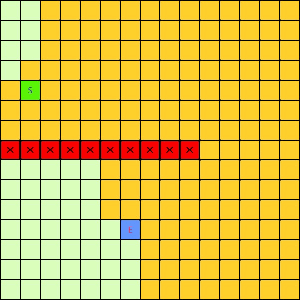 |
 |
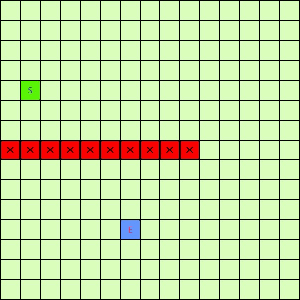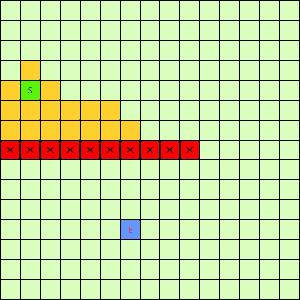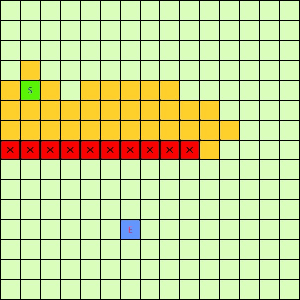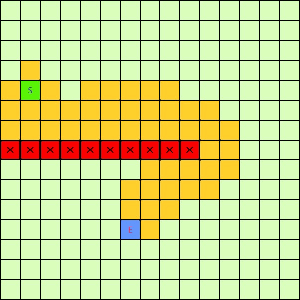 |
| Depth-First | Breath-First | Best-First |
可以看出有障碍物的时候Best-First也能够巧妙的绕过去再冲向终点,也就是说,这个Best-First是一个方格图上寻路的好方法。一般都能比无脑DFS和BFS访问更少的节点。
根据以上的叙述,我们引入一种对搜索方法的分类:一种叫做Uniformed Search,也就是我们前面提到的无脑搜索BFS/DFS,而Dijkstra算法也属于这一类方法。这种Search的特点是无脑暴力,但有很强的通用性,假如对图没有任何先验知识,例如除了是否访问到之外完全不知道终点的其他信息的话,就只能使用这样的搜寻;另一种叫做Informed Search,又叫启发式(heuristic)搜索,即有先验知识的搜索,例如Best-First。其特点是对终点的位置可以有一些启发的信息,根据这些信息可以有倾向性的去筛选可能的路径。而A*算法,也就属于这一类方法。
| Uniform Search | Informed Search |
| BFS搜寻 | BestFirst搜寻 |
| DFS搜寻 | A*算法 |
| Dijkstra算法 |
在与Dijkstra算法的对比中理解A*算法
在大致了解所谓启发式搜寻之后,再来了解A*算法的寻路思路。在介绍之中,将会与Dijkstra算法紧密结合来进行讲解,毕竟这两个算法关系密切,并且在代码结构变量使用上上高度相似,可以说是亲如父子。假如没有充分了解Dijkstra算法,可以先参考博文“三角网格上的寻路算法Part.1—Dijkstra算法”。
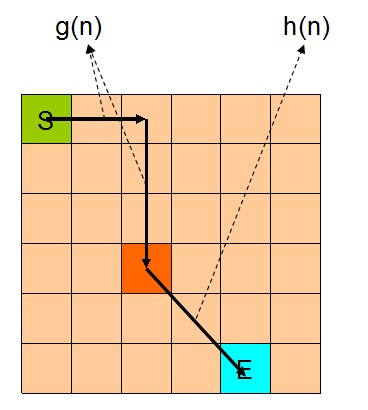
A*与Dijkstra算法最大的不同在于,它采用了启发式估价函数f(n)=g(n)+h(n)。这个g(n)有点类似于distance数组,代表当前节点到n的实际路径长度,而h(n)表示节点n到终点的估算路径长度。在算法实现的时候,f(n)和g(n)也是使用数组来表示,f数组中f[n]表示从S经过n到E的路径当前总估价,g数组中g[n]表示S到n的实际路径长度。而h(n)是和先验信息有关的函数。在我们上面举例的方格图中,h(n)的计算方式就是计算n到E的欧式距离,所以h(n)可以不采用数组,而是保留函数的形式,需要的时候直接计算:
![]()
我们知道Dijkstra算法中,distance数组是一个关键的变量。首先distance值的大小是从容器中取节点的标准,每次选择节点都是选择容器中distance值最小的节点。其次distance值还会在松弛操作中被更新为更小的值。也就是说Dijkstra算法是围绕着distance数组这个核心变量来运行的。而在A*算法中,核心变量则变为f数组,也就是说,A*算法中,我们的选择由distance最小变成了f最小。f数组成为容器的key,每次从容器中选择的是f值最小的节点。
A*算法设置有一个开启列表和关闭列表,节点状态可分为在关闭列表中、在开启列表中与尚未访问到,开启列表与Dijkstra算法中的容器Q类似,而关闭列表也与其相似,能使用bool数组来实现。对节点类别的划分也可以与Dijkstra算法中的A,B,C三类节点分法一一对上号。A*算法的逻辑结构与Dijkstra算法相似度很高,我们可以从下面伪代码的对比中看出:
Function_AStar(图Graph,起点S,终点E) 初始化f数组为MAX。 初始化g数组为MAX。 初始化previus数组为-1。 初始化flagsmap_close数组为false。 初始化开启列表Q。 初始化g[S]=0。 初始化f[S]=h(S)。 将S加入Q。 While(Q不为空)算法结束,若进行到此步则说明未找到终点E P=Q.ExtractMin(),即找到Q中f值最小的点P。 flagsmap_close[P]=true,即设置P为关闭状态(A类节点)。 若P==E 找到终点,算法结束。 对P的所有邻接点n 若n为关闭状态(A类节点),即有flagsmap_close[n]==true continue继续循环。 否则 从S通过P到n的路径长度: |
Function_Dijkstra(图Graph,起点S,终点E) 初始化distance数组为MAX。 初始化previus数组为-1。 初始化flagsmap_close数组为false。 初始化集合Q。 初始化distance[S]=0。 将S加入Q。 While(Q不为空)算法结束,若进行到此步则说明未找到终点E P=Q.ExtractMin(),即找到Q中Distance值最小的点P。 flagsmap_close[p]=true,即设置P为A类节点。 若P==E 找到终点,算法结束。 对P的所有邻接点n 若n为A类节点,即有flagsmap_close[n]==true continue继续循环。 否则 计算从S通过P到n的路径长度: |
| A*算法伪代码 | 上篇博客中Dijkstra算法伪代码 |
涂颜色的代码就是A*和Dijkstra算法不同的地方,可以看出A*与Djikstra有着很多相同的点,例如对节点的分类,对容器Q的使用等。Dijkstra算法是层层向外扩展搜索,而A*算法虽然也是一步步向外搜索,但其扩展的方向更加有倾向性。而正是h函数赋予了A*算法这样的倾向性,一般来说h(n)会设计成在n越与E接近时越小,直到h(E)=0。在A*迭代的过程中,每个节点的f值会越来越与实际路径总长度接近,而g值则起到类似Dijkstra算法中distance的作用。
其他的讨论
关于A*算法正确性证明,博主也曾经想通过类似于Dijkstra算法那样简单的方式去证明,不过似乎是行不通的,经过一番搜索之后,发现一些有益的资源:
论文:Generalized Best-First Search Strategies and the Optimality of A*
尤其是形式化的证明可以从初始论文中找到,证明过程比较复杂,至于你看没看懂,反正我是没有看懂 ╮(╯▽╰)╭,呵呵~
关于A*算法伪代码中有一些比较权威的版本,例如维基百科的版本:
function A*(start,goal) closedset := the empty set //已经被估算的节点集合 openset := set containing the initial node //将要被估算的节点集合 came_from := empty map g_score[start] := 0 //g(n) h_score[start] := heuristic_estimate_of_distance(start, goal) //h(n) f_score[start] := h_score[start] //f(n)=h(n)+g(n),由于g(n)=0,所以…… while openset is not empty //当将被估算的节点存在时,执行 x := the node in openset having the lowest f_score[] value //取x为将被估算的节点中f(x)最小的 if x = goal //若x为终点,执行 return reconstruct_path(came_from,goal) //返回到x的最佳路径 remove x from openset //将x节点从将被估算的节点中删除 add x to closedset //将x节点插入已经被估算的节点 foreach y in neighbor_nodes(x) //对于节点x附近的任意节点y,执行 if y in closedset //若y已被估值,跳过 continue tentative_g_score := g_score[x] + dist_between(x,y) //从起点到节点y的距离 if y not in openset //若y不是将被估算的节点 add y to openset //将y插入将被估算的节点中 tentative_is_better := true elseif tentative_g_score < g_score[y] //如果y的估值小于y的实际距离 tentative_is_better := true //暂时判断为更好 else tentative_is_better := false //否则判断为更差 if tentative_is_better = true //如果判断为更好 came_from[y] := x //将y设为x的子节点 g_score[y] := tentative_g_score h_score[y] := heuristic_estimate_of_distance(y, goal) f_score[y] := g_score[y] + h_score[y] return failure
仔细分析不难得出这份伪代码的逻辑和本文的是一样的。不过需要指出,从网上搜索A*算法会有各种各样的版本,不过笔者发现所有的版本其逻辑可以归结为两类,其区别是对在关闭列表中节点的处理,例如下面的版本:
1:Put the start node, s, on a list called OPEN of unexpanded nodes 2:if |OPEN| = 0 then 3: Exit—no solution exists 4:Remove a node n from OPEN, at which f = g + h is minimum and place it on a list called CLOSED 5:if n is a goal node then 6: Exit with solution 7:Expand node n, generating all its successors with pointers back to n 8:for all successor n0of n do 9: Calculate f(n0) 10: if n0/ ∈ OPEN AND n0/ ∈ CLOSED then 11: Add n0to OPEN 12: Assign the newly computed f(n0) to node n0 13: else 14: If new f(n0) value is smaller than the previous value, then update with the new value (and predecessor) 15: If n0 was in CLOSED, move it back to OPEN 16:Go to (2)
总之就是部分版本对于close列表中的节点还会进行更新处理并重新加入开启列表,而另一部分版本是continue即什么都不做。咋一看这两者逻辑截然不同,那是不是有对于不对呢?其实这一区别主要和h函数有关。需要强调的是,A*算法的计算过程很大程度依赖于h函数的设计,一般来说h函数总会设计成h(n)<=Real(n),即n到E的实际距离。这样A*算法总会找到最短路径,这是存在证明的,论文里也提到过。假如h函数是一致单调的,例如对于两个节点n和m,若h(n)<h(m)能推出Real(n)<Real(m),则两个版本的伪代码是全部等价的。否则只有第二个版本是完备的,也就是需要重新加符合条件的closed节点入Open。Amitp在他的一篇关于A*的长篇文章中也指出这个h函数在consistant和admissible的时候,两份伪代码等价。通常我们将A*运用在实际模型的寻路上,例如三角网或者方格图,这些模型都是在欧式几何空间中很直观的模型,很多点和线都是具有实际几何意义的。在这类模型上,我们都知道两点之间线段最短的公理,因而采用欧式距离作为估计是很合理的。
有很多关于A*的很详细的细节讨论可以从amitp的博客上获取,尤其是一些小应用很好玩,有兴趣的人可以尝试一下,这里贴出其中一个flash,不能运行的话可以刷新一下,注意这个起点需要鼠标拖动与终点分离。
实现代码
A*算法的实现和上篇Dijkstra算法的实现是在同一个工程项目里,其测试用例都是用算法去求三角网格测地线。AbstractGraph,Mesh以及读取文件的类型可以参考上一篇博文。本文主要的关键是A*的逻辑。这里的类GeodeticCalculator_AStar是算法的执行主逻辑类,其中容器采用和Dijkstra算法一模一样的堆,这个堆唯一的不同就是key由从distance数组获取改为从f数组获取。
Dijkstra算法与A*算法通用的二叉堆容器实现的代码:
#ifndef ASTAROPENSET_H #define ASTAROPENSET_H #include <vector> #include <math.h> #include "DijkstraSet.h" class AStarSet_Heap:DijkstraSet { private: std::vector<int> heapArray; std::vector<float> *f_key; std::vector<int> indexInHeap;// stores the index to heapArray for each vertexIndex, -1 if not exist public: AStarSet_Heap(int maxsize,std::vector<float> *key) { this->f_key=key; this->indexInHeap.resize(maxsize,-1); } ~AStarSet_Heap(){f_key=0;} void Add(int pindex) { this->heapArray.push_back(pindex); indexInHeap[pindex]=heapArray.size()-1; ShiftUp(heapArray.size()-1); } int ExtractMin() { if(heapArray.size()==0) return -1; int pindex=heapArray[0]; Swap(0,heapArray.size()-1); heapArray.pop_back(); ShiftDown(0); indexInHeap[pindex]=-1; return pindex; } bool IsEmpty() { return heapArray.size()==0; } void DecreaseKey(int pindex) { ShiftUp(indexInHeap[pindex]); } private: int GetParent(int index) { return (index-1)/2; } int GetLeftChild(int index) { return 2*index+1; } int GetRightChild(int index) { return 2*index+2; } bool IsLessThan(int index0,int index1) { return (*f_key)[heapArray[index0]]<(*f_key)[heapArray[index1]]; } void ShiftUp(int i) { if (i == 0) return; else { int parent = GetParent(i); if (IsLessThan(i,parent)) { Swap(i, parent); ShiftUp(parent); } } } void ShiftDown(int i) { if (i >= heapArray.size()) return; int min = i; int lc = GetLeftChild(i); int rc = GetRightChild(i); if (lc < heapArray.size() && IsLessThan(lc,min)) min = lc; if (rc < heapArray.size() && IsLessThan(rc,min)) min = rc; if (min != i) { Swap(i, min); ShiftDown(min); } } void Swap(int i, int j) { int temp = heapArray[i]; heapArray[i] = heapArray[j]; heapArray[j] = temp; indexInHeap[heapArray[i]]=i;//record new position indexInHeap[heapArray[j]]=j;//record new position } }; #endif
算法主体:
#ifndef GEODETICCALCULATOR_ASTAR_H #define GEODETICCALCULATOR_ASTAR_H #include <vector> #include <math.h> #include "Mesh.h" #include "AStarOpenSet.h" class GeodeticCalculator_AStar { private: AbstractGraph& graph; int startIndex; int endIndex; std::vector<float> gMap;//current s-distances for each node std::vector<float> fMap;//current f-distances for each node std::vector<int> previus;//previus vertex on each vertex's s-path AStarSet_Heap* set_Open;//current involved vertices, every vertex in set has a path to start point with distance<MAX_DIS but may not be s-distance. std::vector<bool> flagMap_Close;//indicates if the s-path is found std::vector<bool> visited;//record visited vertices; std::vector<int> resultPath;//result path from start to end public: GeodeticCalculator_AStar(AbstractGraph& g,int vstIndex,int vedIndex):graph(g),startIndex(vstIndex),endIndex(vedIndex) { set_Open=0; } ~GeodeticCalculator_AStar() { if(set_Open!=0) delete set_Open; } //core functions bool Execute()//main function execute AStar, return true if the end point is reached,false if path to end not exist { visited.resize(graph.GetNodeCount(),false); gMap.resize(graph.GetNodeCount(),MAX_DIS); fMap.resize(graph.GetNodeCount(),MAX_DIS); previus.resize(graph.GetNodeCount(),-1); flagMap_Close.resize(graph.GetNodeCount(),false); this->set_Open=new AStarSet_Heap(graph.GetNodeCount(),&fMap); set_Open->Add(startIndex); gMap[startIndex]=0; fMap[startIndex]=GetH(startIndex); while(!set_Open->IsEmpty()) { int pindex=set_Open->ExtractMin();// vertex with index "pindex" found its s-path flagMap_Close[pindex]=true;//mark it if(pindex==endIndex) return true; UpdateNeighborMinDistance(pindex);// update its neighbor's s-distance } return false; } private: //core functions float GetH(int p1) { return graph.GetEvaDistance(p1,endIndex); }//calculate h[p1] when needed, not necessary to create an array to store void UpdateNeighborMinDistance(int pindex) { std::vector<int>& neightbourlist=graph.GetNeighbourList(pindex); for(size_t i=0;i<neightbourlist.size();i++ ) { int neighbourindex=neightbourlist[i]; visited[neighbourindex]=true;//just for recording , not necessary if (flagMap_Close[neighbourindex])//if Close Nodes,Type A { continue; } else { float gPassp = gMap[pindex] + graph.GetWeight(pindex, neighbourindex); if (fMap[neighbourindex]==MAX_DIS)//if unvisited nodes ,Type C { //same operation as in Dijkstra except the assignment of fMap gMap[neighbourindex] = gPassp; fMap[neighbourindex]=gPassp + GetH(neighbourindex); previus[neighbourindex] = pindex; set_Open->Add(neighbourindex); } else { //same operation as in Dijkstra except the assignment of fMap if (gPassp < gMap[neighbourindex])//Type B { gMap[neighbourindex] = gPassp; fMap[neighbourindex]=gPassp + GetH(neighbourindex); previus[neighbourindex] = pindex; set_Open->DecreaseKey(neighbourindex); } } } } }// for neighbors of pindex ,execute relaxation operation public: //extra functions std::vector<int>& GetPath() { int cur=endIndex; while(cur!=startIndex) { resultPath.push_back(cur); cur=previus[cur]; } resultPath.push_back(startIndex); std::reverse(resultPath.begin(),resultPath.end()); return resultPath; }// reconstruct path from prev[] float PathLength() { return gMap[endIndex]; }//return the length of the path form result path int VisitedNodeCount() { return (int)std::count(visited.begin(),visited.end(),true); }//return the visited nodes count std::vector<bool>& GetVisitedFlags() { return visited; }//return the visited flags of the nodes }; #endif
对比代码结构发现与Dijkstra算法简直不能再像,所以说先若是先了解了Dijkstra算法,那么只要做小的代码改动就能变成A*。
算法效果
因为我们始终强调A*改进了Djikstra算法的访问节点次数,所以我们可以使用两个模型的运行实际例子来说明。首先是计算测地线距离,上篇文章中我们就已经算出了Dijkstra的最短路径,其中访问过的节点都涂成绿色了,这次采用A*算法,可以看出A*算法比起Djikstra算法的确减少了节点的访问。
 |
| Dijkstra算法寻找的测地线以及访问过的节点 |
 |
| A*算法寻找的测地线以及访问过的节点 |
我们再换一个方格图的模型如下,在这个模型上我们再做一些试验:
 |
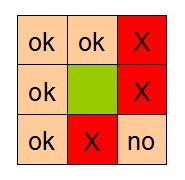 |
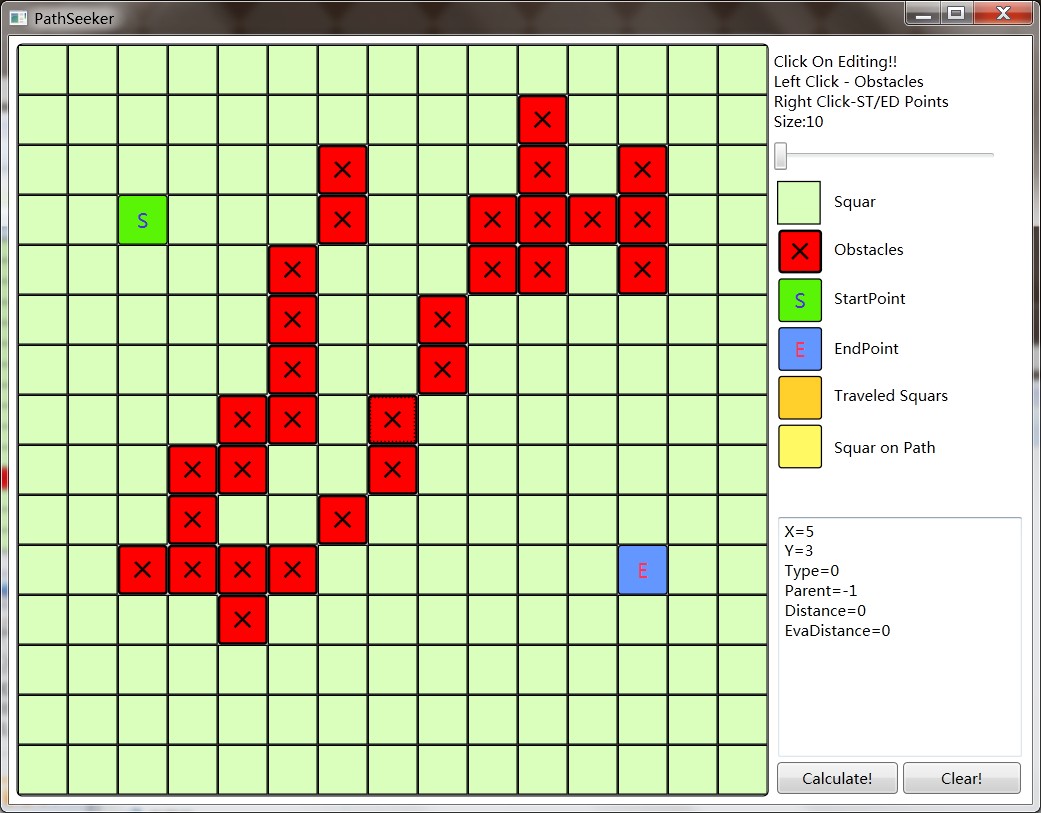
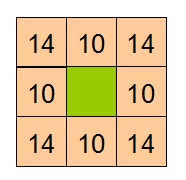
| 8个邻域其权值 | 邻接关系,ok表示邻接no表示不邻接X表示障碍物 |
这个小软件PathSeeker是博主使用WPF写的一个算法可视化小工具,可以用鼠标设置方格图大小以及起点终点和障碍物,还能够选择BFS,Dijkstra算法,A*算法来计算路径和显示参数。
WPF小工具PathSeeker下载地址:https://files.cnblogs.com/chnhideyoshi/PathSeeker.rar
PathSeeker可以显示A*与Djikstra算法对每个访问到的节点所设置的distance值、g值、f值、h值等。方格寻路时能够寻找八邻域方格,八个领域方格的边权值不一样,而且不容许从角落穿出去。
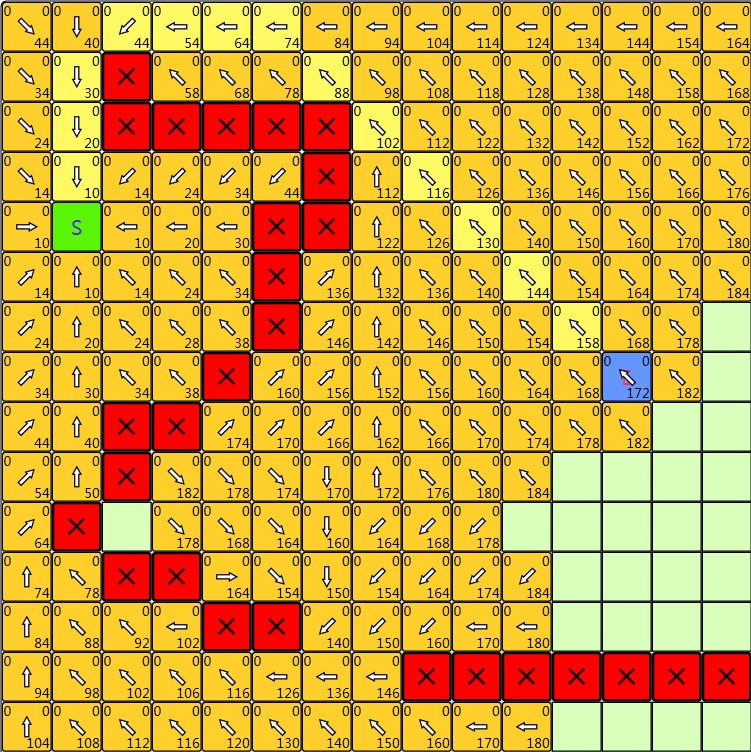 |
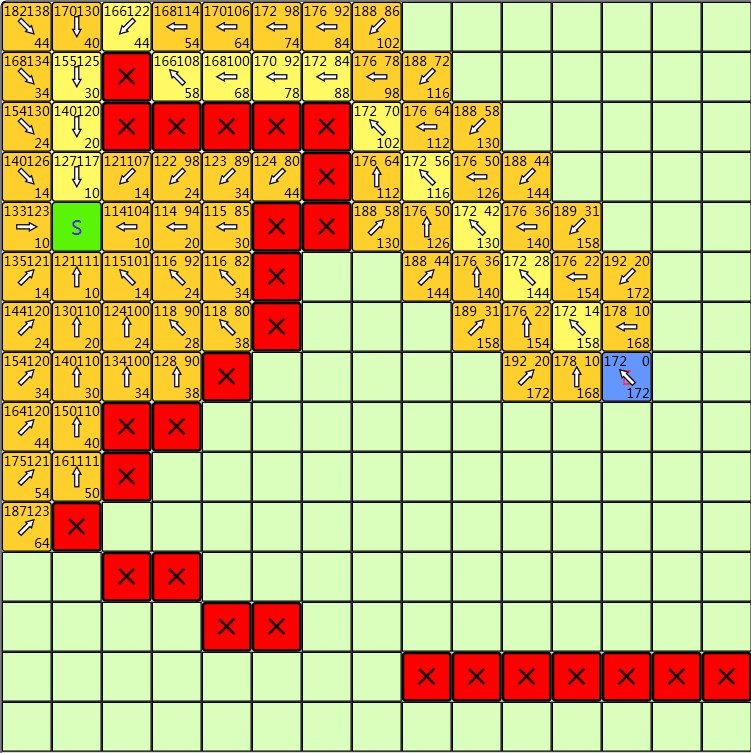 |
| Dijkstra算法寻路结果,方块右下角为distance值 | A*算法寻路结果,方块左上、右上和右下分别对应f值、h值和g值 |
从上述结果的确可以看出A*相对Dijkstra的改善,值得注意的是A*与Dijkstra都能找到最短,如果最短路径不止一条两个算法的最短路径不完全是一模一样的,但是路径长度会是一样的。
最后提供一下所有源代码的维护地址:
计算三角网近似测地线代码工程: https://github.com/chnhideyoshi/SeededGrow2d/tree/master/MeshGeodetic
PathSeeker代码工程:https://github.com/chnhideyoshi/SeededGrow2d/tree/master/PathSeeker