20182334 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
第十周我学习到的内容有:
- 有向图、无向图和完全图及带权概念
- 图的广度优先遍历和深度优先遍历
- 最小生成树
- 邻接矩阵和邻接表
- 哈希方法
无向图
无向图中表示边的顶点对是无序的。
如果图中两个顶点之间有边连接,则称它们是邻接的。

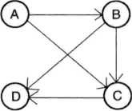
如图所示,A与B是邻接的,而顶点A和D不是邻接的。
有向图
在有向图中,边是顶点的有序对。
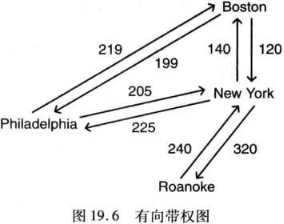
有向图中的 路径是连接图中两个顶点的有向边的序列。在无向图中,路径A、B、D 是从A到D的路径,在有向图中这仍然是一条路径。但有向图中的路 径不是双向的,所以反过来不再成立:D、B、A不是从D到A的有效路径。
有向图中的路径是连接图中两个顶点的有向边的序列。
完全图
含有最多条边的无向图称为完全图。对于第一个顶点来说,它需要(n-1)条边与 其他顶点相连。对于第二个顶点来说,它只需要(n-2)条边,因为它已经与第一个顶点相连了。
如果无向图中连接顶点的边数达到最大,则图为完全图。实际上,图就是树。
带权图
图的每条边上都有对应的权值的图称为带权图。
放两张图应该很容易理解

图的广度优先遍历和深度优先遍历
深度优先遍历
无向图的深度优先遍历图解
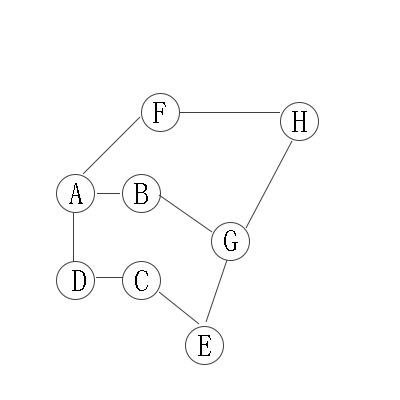
对上无向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问B(A的邻接点)。 在第1步访问A之后,接下来应该访问的是A的邻接点,即"B,D,F"中的一个。但在本文的实现中,顶点ABCDEFGH是按照顺序存储,B在"D和F"的前面,因此,先访问B。
第3步:访问G(B的邻接点)。 和B相连只有"G"(A已经访问过了)
第4步:访问E(G的邻接点)。 在第3步访问了B的邻接点G之后,接下来应该访问G的邻接点,即"E和H"中一个(B已经被访问过,就不算在内)。而由于E在H之前,先访问E。
第5步:访问C(E的邻接点)。 和E相连只有"C"(G已经访问过了)。
第6步:访问D(C的邻接点)。
第7步:访问H。因为D没有未被访问的邻接点;因此,一直回溯到访问G的另一个邻接点H。
第8步:访问(H的邻接点)F。
因此访问顺序是:A -> B -> G -> E -> C -> D -> H -> F
有向图的深度优先遍历

对上有向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问(A的出度对应的字母)B。 在第1步访问A之后,接下来应该访问的是A的出度对应字母,即"B,C,F"中的一个。但在本文的实现中,顶点ABCDEFGH是按照顺序存储,B在"C和F"的前面,因此,先访问B。
第3步:访问(B的出度对应的字母)F。 B的出度对应字母只有F。
第4步:访问H(F的出度对应的字母)。 F的出度对应字母只有H。
第5步:访问(H的出度对应的字母)G。
第6步:访问(G的出度对应字母)E。 在第5步访问G之后,接下来应该访问的是G的出度对应字母,即"B,C,E"中的一个。但在本文的实现中,顶点B已经访问了,由于C在E前面,所以先访问C。
第7步:访问(C的出度对应的字母)D。
第8步:访问(C的出度对应字母)D。 在第7步访问C之后,接下来应该访问的是C的出度对应字母,即"B,D"中的一个。但在本文的实现中,顶点B已经访问了,所以访问D。
第9步:访问E。D无出度,所以一直回溯到G对应的另一个出度E。
因此访问顺序是:A -> B -> F -> H -> G -> C -> D -> E
广度优先遍历
无向图的广度优先遍历:
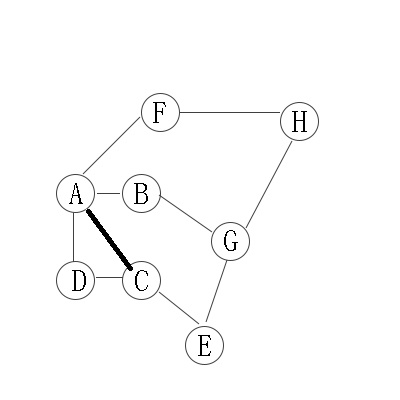
从A开始,有4个邻接点,“B,C,D,F”,这是第二层;
在分别从B,C,D,F开始找他们的邻接点,为第三层。以此类推。
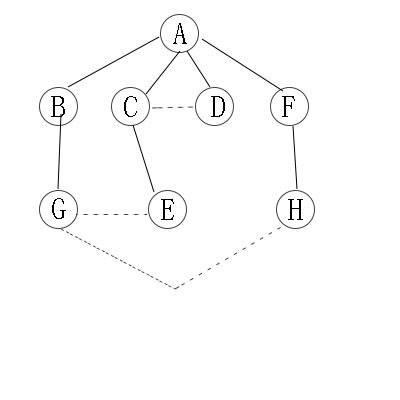
因此访问顺序是:A -> B -> C -> D -> F -> G -> E -> H
有向图的广度优先遍历图解:
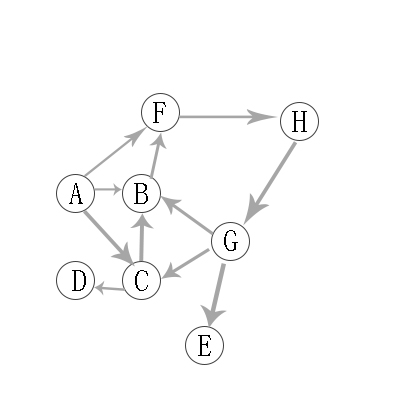
与无向图类似 。可以参考。
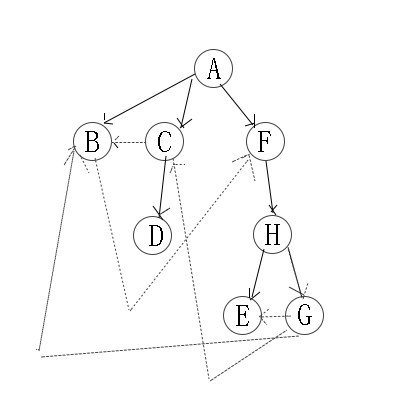
因此访问顺序是:A -> B -> C -> F -> D -> H -> E -> G
以上内容部分来自图的深度优先遍历(DFS)和广度优先遍历(BFS)算法分析
图的深度优先遍历与广度优先遍历的主要差异在于用栈代替队列来管理遍历过程。
最小生成树
学了两种方法:
- Kruskal算法
- Prim算法
Kruskal算法
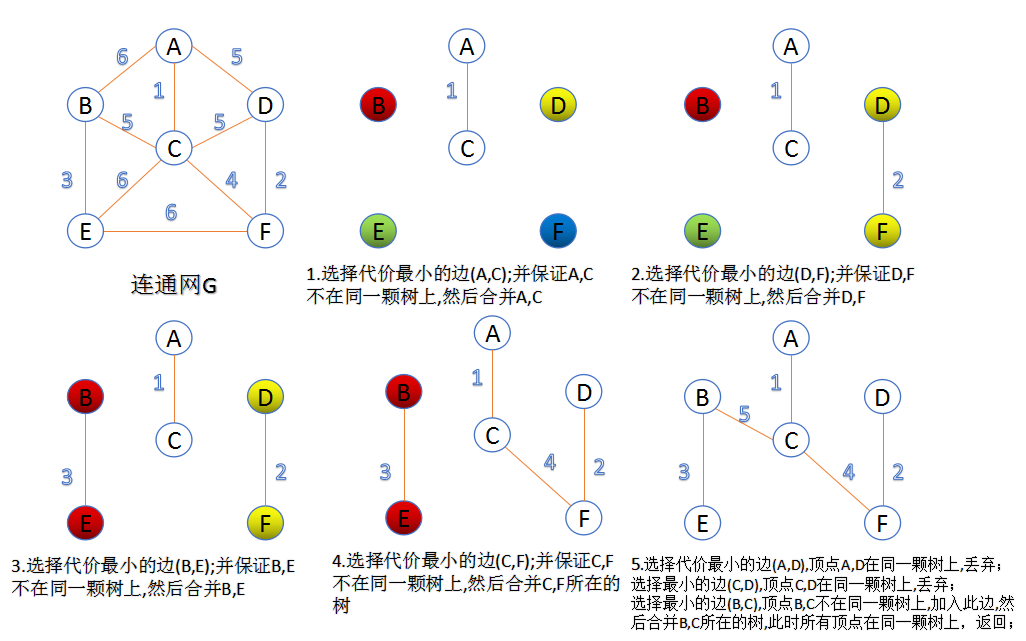
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点看成独立的n棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
- 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
Prim算法
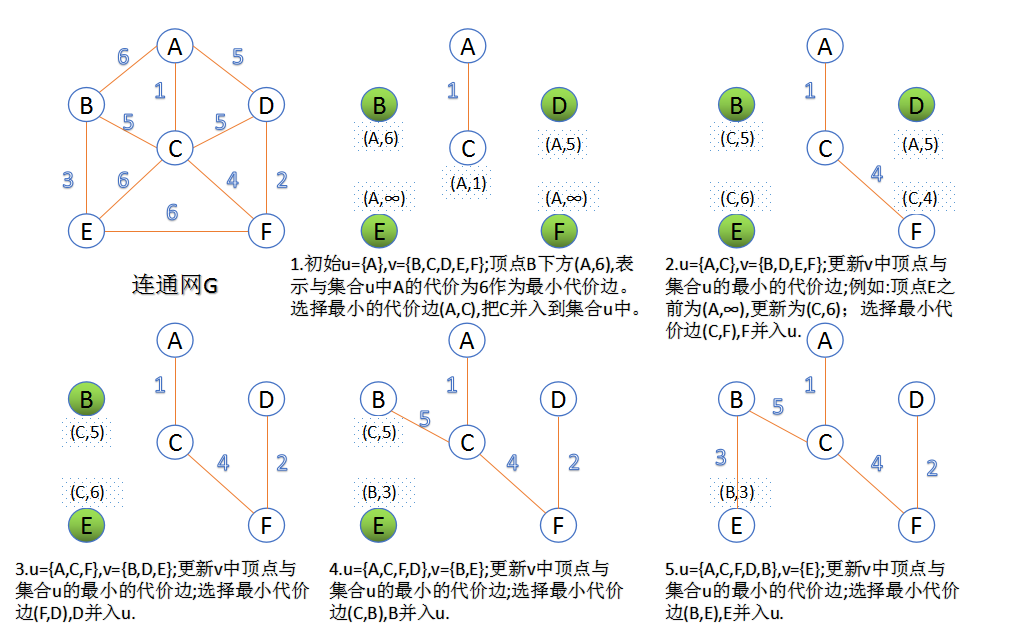
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为VV;初始令集合u={s},v=V−uu={s},v=V−u;
- 在两个集合u,vu,v能够组成的边中,选择一条代价最小的边(u0,v0)(u0,v0),加入到最小生成树中,并把v0v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:

看一个实例,下图左就是一个无向图。
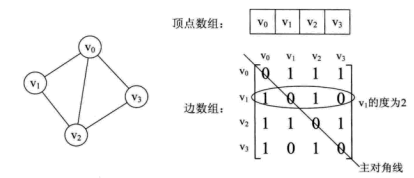
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从这个矩阵中,很容易知道图中的信息。
- 要判断任意两顶点是否有边无边就很容易了;
- 要知道某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
- 求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点;
而有向图讲究入度和出度,顶点vi的入度为1,正好是第i列各数之和。顶点vi的出度为2,即第i行的各数之和。
若图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
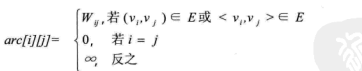
代码实现:
public class asd {
public static void main(String[] args) {
int a[] = {0,1,2,3,4};
int b[][] = new int[5][5];
int i=0,j,count = 0;
Scanner in = new Scanner(System.in);
System.out.println("V(" + i + "):");
for(i = 0;i < 5;i++){
for(j = 0 ;j < 5 ; j++){
b[i][j] = in.nextInt();
}
if(i < 4)
{
System.out.println("V(" + (i+1) + "): ");
}
}
for(i = 0;i < 5;i++){
System.out.print("V(" + i + "): ");
for(j = 0 ;j < 5 ; j++){
System.out.print( b[i][j] + " " );;
}
System.out.println();
}
for(i = 0;i < 5;i++){
count = 0;
System.out.print("V(" + i + ")的出度为: ");
for(j = 0 ;j < 5 ; j++){
if(b[i][j] != 0){
count++;
}
//System.out.print( b[i][j] + " " );;
}
System.out.println(count);
}
System.out.println();
System.out.println();
for(i = 0;i < 5;i++){
count = 0;
System.out.print("V(" + i + ")的入度为: ");
for(j = 0 ;j < 5 ; j++){
if(b[j][i] != 0){
count++;
}
//System.out.print( b[i][j] + " " );;
}
System.out.println(count);
}
}
}
邻接表
邻接矩阵是不错的一种图存储结构,但是,对于边数相对顶点较少的图,这种结构存在对存储空间的极大浪费。因此,找到一种数组与链表相结合的存储方法称为邻接表。
邻接表的处理方法是这样的:
- 图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过,数组可以较容易的读取顶点的信息,更加方便。
- 图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
例如,下图就是一个无向图的邻接表的结构。
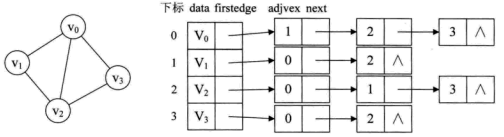
从图中可以看出,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可。如下图所示。
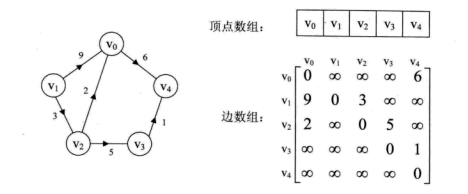
哈希方法
Hash
Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入,通过散列算法,变换成固定长度的输出,该输出就是散列值。根据散列值作为地址存放数据,这种转换是一种压缩映射,简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。查找关键字数据(如K)的时候,若结构中存在和关键字相等的记录,则必定在f(K)的存储位置上。由此,不需比较便可直接取得所查记录。我们称这个对应关系f为散列函数(Hash function),按这个事件建立的表为散列表。
综上所述,根据散列函数f(key)和处理冲突的方法将一组关键字映象到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“象” 作为记录在表中的存储位置,这种表便称为散列表,这一映象过程称为散列造表或散列,所得的存储位置称散列地址。
Hash冲突
对不同的关键字可能得到同一散列地址,即key1≠key2,而f(key1)=f(key2),这种现象称hash冲突。即:key1通过f(key1)得到散列地址去存储key1,同理,key2发现自己对应的散列地址已经被key1占据了。
解决办法(总共有四种):
- 1.开放寻址法
所谓的开放定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入 。
开放寻址法:Hi=(H(key) + di) MOD m,i=1,2,…,k(k<=m-1),其中H(key)为散列函数,m为散列表长,di为增量序列,可有下列三种取法:
- di=1,2,3,…,m-1,称线性探测再散列;
- di=12,(-1)2,22,(-2)2,(3)2,…,±(k)2,(k<=m/2)称二次探测再散列;
- di=伪随机数序列,称伪随机探测再散列。
用开放定址法解决冲突的做法是:当冲突发生时,使用某种探测技术(线性探测法、二次探测法(解决线性探测的堆积问题)、随机探测法(和二次探测原理一致,不一样的是:二次探测以定值跳跃,而随机探测的散列地址跳跃长度是不定值))在散列表中形成一个探测序列。沿此序列逐个单元地查找,直到找到给定的关键字,或者碰到一个开放的地址(即该地址单元为空)为止插入即可。
比如说,我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,34},表长为12。 我们用散列函数f(key) = key mod l2
当计算前S个数{12,67,56,16,25}时,都是没有冲突的散列地址,直接存入:

计算key = 37时,发现f(37) = 1,此时就与25所在的位置冲突。
于是我们应用上面的公式f(37) = (f(37)+1) mod 12 = 2。于是将37存入下标为2的位置:

-
2.再哈希
再哈希法又叫双哈希法,有多个不同的Hash函数,当发生冲突时,使用第二个,第三个,….,等哈希函数去计算地址,直到无冲突。虽然不易发生聚集,但是增加了计算时间。 -
3.链地址法(Java hashmap就是这么做的)
链地址法的基本思想是:每个哈希表节点都有一个next指针,多个哈希表节点可以用next指针构成一个单向链表,将所有关键字为同义词的结点链接在同一个单链表中,如:
设有 m = 5 , H(K) = K mod 5 ,关键字值序例 5 , 21 , 17 , 9 , 15 , 36 , 41 , 24 ,按外链地址法所建立的哈希表如下图所示:
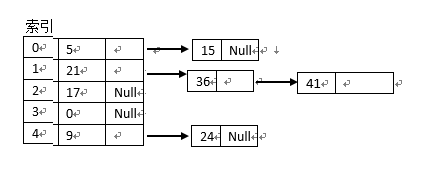
-
4.建立一个公共溢出区
这种方法的基本思想是:将哈希表分为基本表和溢出表两部分,凡是和基本表发生冲突的元素,一律填入溢出表
教材学习中的问题和解决过程
- 问题1:在计算深度优先遍历的时候,不明白当一条路走到头后是直接倒回来遍历还是先倒回来再遍历?
- 问题1解决方案:可以把其理解为栈,下面有个例子,可以理解下:
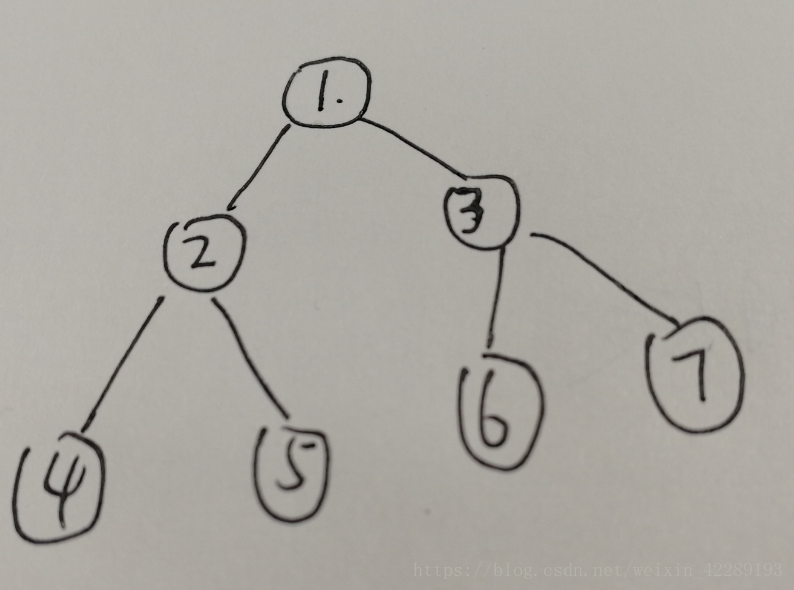
深度优先搜索的步骤为:
(1)、首先节点 1 进栈,节点1在栈顶;
(2)、然后节点1出栈,访问节点1,节点1的孩子节点3进栈,节点2进栈;
(3)、节点2在栈顶,然后节点2出栈,访问节点2
(4)、节点2的孩子节点5进栈,节点4进栈
(5)、节点4在栈顶,节点4出栈,访问节点4,
(6)、节点4左右孩子为空,然后节点5在栈顶,节点5出栈,访问节点5;
(7)、节点5左右孩子为空,然后节点3在站顶,节点3出栈,访问节点3;
(8)、节点3的孩子节点7进栈,节点6进栈
(9)、节点6在栈顶,节点6出栈,访问节点6;
(10)、节点6的孩子为空,这个时候节点7在栈顶,节点7出栈,访问节点7
(11)、节点7的左右孩子为空,此时栈为空,遍历结束。
- 问题2:对于邻接矩阵概念还较清楚,但是到邻接表这里就有点不清楚他的实现过程,或者说是基本不太懂。
- 问题2解决方案:上网看到一篇博客:数据结构:图的存储结构之邻接表 ,里面详细的介绍了邻接表的概念以及如何使用,有c++的代码,可以自己参考,用java再实现一遍。
代码调试中的问题和解决过程
- 问题1:不知道如何构建图。
- 问题1解决方案:上网看了看,发现了一个方法,代码如下:
import java.util.Stack;
import static sun.java2d.cmm.ColorTransform.In;
public class Graph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V;
private int E;
private Bag<Integer>[] adj;
public Graph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");
this.V = V;
this.E = 0;
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
}
public Graph(In in) {
this(in.readInt());
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
addEdge(v, w);
}
}
public Graph(Graph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < G.V(); v++) { // reverse so that adjacency list is in same order as original
Stack<Integer> reverse = new Stack<Integer>();
for (int w : G.adj[v]) {
reverse.push(w);
}
for (int w : reverse) {
adj[v].add(w);
}
}
}
public int V() {
return V;
}
public int E() {
return E;
}
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IndexOutOfBoundsException("vertex " + v + " is not between 0 and " + (V-1));
}
public void addEdge(int v, int w) {
validateVertex(v);
validateVertex(w);
E++;
adj[v].add(w);
adj[w].add(v);
}
public int degree(int v) {
validateVertex(v);
return adj[v].size();
}
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " vertices, " + E + " edges " + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (int w : adj[v]) {
s.append(w + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
public static void main(String[] args) {
In in = new In(args[0]);
Graph G = new Graph(in);
StdOut.println(G);
}
}
-
问题2:在实现邻接矩阵的时候,遇到不清楚如何表示横纵两种数据,两个牌子,一套数据,知道应该用二维数组,但是实现起来还是遇到了困难,不知道该如何实现?
-
问题2解决方案:代码如下:
public class asd {
public static void main(String[] args) {
int a[] = {0,1,2,3,4};
int b[][] = new int[5][5];
int i=0,j,count = 0;
Scanner in = new Scanner(System.in);
System.out.println("V(" + i + "):");
for(i = 0;i < 5;i++){
for(j = 0 ;j < 5 ; j++){
b[i][j] = in.nextInt();
}
if(i < 4)
{
System.out.println("V(" + (i+1) + "): ");
}
}
for(i = 0;i < 5;i++){
System.out.print("V(" + i + "): ");
for(j = 0 ;j < 5 ; j++){
System.out.print( b[i][j] + " " );;
}
System.out.println();
}
for(i = 0;i < 5;i++){
count = 0;
System.out.print("V(" + i + ")的出度为: ");
for(j = 0 ;j < 5 ; j++){
if(b[i][j] != 0){
count++;
}
//System.out.print( b[i][j] + " " );;
}
System.out.println(count);
}
System.out.println();
System.out.println();
for(i = 0;i < 5;i++){
count = 0;
System.out.print("V(" + i + ")的入度为: ");
for(j = 0 ;j < 5 ; j++){
if(b[j][i] != 0){
count++;
}
//System.out.print( b[i][j] + " " );;
}
System.out.println(count);
}
}
}
package LinjieJuzheng;
import java.util.Scanner;
public class Noasd {
public static void main(String[] args) {
//int a[] = {0,1,2,3,4};
int b[][] = new int[5][5];
int i=0,j,count = 0;
Scanner in = new Scanner(System.in);
System.out.println("V(" + i + "):");
for(i = 0;i < 5;i++){
for(j = 0 ;j < 5 ; j++){
b[i][j] = in.nextInt();
}
if(i < 4)
{
System.out.println("V(" + (i+1) + "): ");
}
}
for(i = 0;i < 5;i++){
System.out.print("V(" + i + "): ");
for(j = 0 ;j < 5 ; j++){
System.out.print( b[i][j] + " " );;
}
System.out.println();
}
for(i = 0;i < 5;i++){
count = 0;
System.out.print("V(" + i + ")的出度为: ");
for(j = 0 ;j < 5 ; j++){
if(b[i][j] != 0){
count++;
}
//System.out.print( b[i][j] + " " );;
}
System.out.println(count);
}
System.out.println();
System.out.println();
for(i = 0;i < 5;i++){
count = 0;
System.out.print("V(" + i + ")的入度为: ");
for(j = 0 ;j < 5 ; j++){
if(b[j][i] != 0){
count++;
}
//System.out.print( b[i][j] + " " );;
}
System.out.println(count);
}
}
}
代码托管

上周考试错题总结
上周无考试
点评过的同学博客和代码
其他(感悟、思考等)
已经打到10000行了,还有一个月,争取再干5000行。在这一学期的学习中,基本把所有学习的时间都给了java,但是很充实,也很 痛苦,但并快乐着。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 212/212 | 2/2 | 17/17 | |
| 第二周 | 132/344 | 2/4 | 17/34 | |
| 第三周 | 689/1033 | 1/5 | 23/67 | |
| 第四周 | 664/1697 | 2/7 | 20/87 | |
| 第五周 | 586/2283 | 2/9 | 20/107 | |
| 第六周 | 500/2783 | 1/10 | 26/133 | |
| 第七周 | 2143 /4928 | 2/12 | 40/173 | |
| 第八周 | 2000 /6140 | 2/14 | 40/210 | |
| 第九周 | 4000 /10140 | 2/16 | 40/250 | |
| 第十周 | 1032/11172 | 2/18 | 40/290 |
-
计划学习时间:29小时
-
实际学习时间:40小时
-
改进情况:不妥协,死磕到底!
参考资料
-
[《Java程序设计与数据结构教程(第二版)》学习指导](http://www.cnblogs.com/rocedu/p/5182332.html