【问题描述】
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
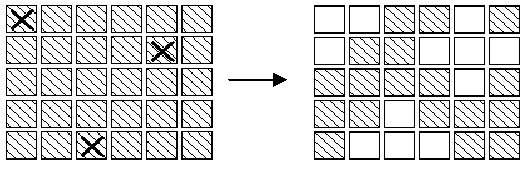
The aim of the game is, starting from any initial set of lights on
in the display, to press buttons to get the display to a state where all
lights are off. When adjacent buttons are pressed, the action of one
button can undo the effect of another. For instance, in the display
below, pressing buttons marked X in the left display results in the
right display.Note that the buttons in row 2 column 3 and row 2 column 5
both change the state of the button in row 2 column 4,so that, in the
end, its state is unchanged.
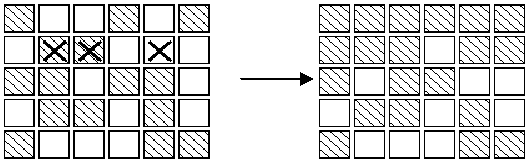
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the
effect of the first press, so no button ever need be pressed more than
once.
3. As illustrated in the second diagram, all the lights in the first
row may be turned off, by pressing the corresponding buttons in the
second row. By repeating this process in each row, all the lights in the
first
four rows may be turned out. Similarly, by pressing buttons in
columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
【输入格式】
【输出格式】
【输入样例】
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
【输出样例】
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
正解:高斯消元法
解题报告:这是最裸的高斯消元。。。
1 #include <iostream> 2 #include <iomanip> 3 #include <algorithm> 4 #include <cstdlib> 5 #include <cstdio> 6 #include <cmath> 7 #include <cstring> 8 #include <string> 9 #define RG register 10 11 using namespace std; 12 13 int gi(){ 14 char ch=getchar();RG int x=0; 15 while(ch<'0' || ch>'9') ch=getchar(); 16 while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); 17 return x; 18 } 19 20 int x[35],a[35][35]; 21 22 int main(){ 23 freopen("gauss.in","r",stdin); 24 freopen("gauss.out","w",stdout); 25 RG int n=gi(),tot=0; 26 while(n--){ 27 for (RG int i=1; i<=5; i++){ 28 RG int s=(i-1)*6; 29 for (RG int j=1; j<=6; j++){ 30 RG int k=s+j; 31 a[k][k]=1; 32 if (k>6) a[k][k-6]=1; 33 if (k%6) a[k][k+1]=1; 34 if (k%6!=1) a[k][k-1]=1; 35 if (k<25) a[k][k+6]=1; 36 } 37 } 38 for (RG int i=1; i<=5; ++i){ 39 RG int s=(i-1)*6; 40 for (RG int j=1; j<=6; ++j) 41 a[s+j][31]=gi(); 42 } 43 for (RG int i=1; i<=30; ++i){ 44 RG int k=i; 45 for (; k<=30; ++k) 46 if (a[k][i]) break; 47 for (RG int j=1; j<=31; j++) 48 swap(a[i][j],a[k][j]); 49 for (RG int j=1; j<=30; j++) 50 if (i!=j && a[j][i]) 51 for (k=1; k<=31; k++) 52 a[j][k]=a[i][k]^a[j][k]; 53 } 54 printf("PUZZLE #%d ",++tot); 55 for (RG int i=1; i<=30; i++){ 56 printf("%d",a[i][31]); 57 if (i%6==0) printf(" "); 58 else printf(" "); 59 } 60 } 61 return 0; 62 }