今天看到这篇文章。颇为震撼。感叹算法之“神通”。
借助于合适的算法能够完毕看似不可能的事情。
最早这个问题是在Stack Overflow站点上面给出的(Sorting numbers in RAM):

题目:
提供一个1M的ROM和1M的RAM,一个输入流和一个输出流。
程序代码终于烧录在1M的ROM中,程序能够使用1M的RAM进行运算。输入流中依次输入100万个8位的整数。要求输出流中输出这100万个数排序后的结果。
已经能够搜索到非常多解法了,今天看到一个国外的程序猿的分析,认为非常有趣,想把他的分析过程简单转在这里。简单一看,根本不可能。100万个8位数不管怎样也不能在1M的内存里装下。
排序过程是利用归并排序。效率较高。最难的地方是在怎样将排序后的100万个数字存下来。换一种思路,不一定要存下每个数字本身,由于数字都已经排序了。那么相邻两个数字之间的差值是非常小的,假设在极端的情况下,两个数字之间的差值非常大,那么必定会有很多其它量的相邻数字之间的差值更小,因此存下全部的100万个数字的差值须要的空间是能够估算的。
平均每个差值的大小为:10^8/100万 = 100,100须要7个bit位来表示,因此共须要100万×7 = 875, 000 字节,不到1M的空间,可是还有非常多大于128的数值须要编码,这样有一些数值的编码大于7个bit。因此,接下来的问题是怎样编码这100万个差值,能尽可能压缩空间,作者举出了算数编码来解决这一问题。选择一种简单的编码规则,即:看第一个bit位,假设是0,则后6个bit位表示数值。假设是1,则表示差值为64,继续读取后一位,假设仍然为1,则差值继续累加1。直到读到0,然后读取后面的6个bit,这样能够表示全部可能出现的值,这样下来,终于计算出所须要的内存为1070312.5bytes,仍然大于1M。
终于採用了一个针对该问题的哈夫曼编码解决。算数编码看懂了,哈夫曼编码也似乎看明确了,可是如何运用到解决本问题中,还不是太明确。
同一时候作者也给出了339行的解决这个问题的实战代码。
以下是详细的解决的方法,本人的翻译能力有限。无法将原文的意思全然的表达,希望读者自己去理解当中的意思。
整体来说,这样的思路绝对是一种超脱俗,绝对的不可思议。
Arithmetic Coding and the 1MB Sorting Problem
It’s been two weeks since the 1MB Sorting Problem was originally featured on Reddit, and in case you don’t think this artificial problem has been thoroughly stomped into the ground yet, here’s a continuation of last post’s explanation of the working C++ program which solves it.
In that post, I gave a high-level outline of the approach, and showed an encoding scheme – which I’ve since learned is Golomb coding – which comes close to meeting the memory requirements, but doesn’t quite fit. Arithmetic coding, on the other hand, does fit. It’s interesting, because this problem, as it was phrased, almost seems designed to force you into arithmetic coding (though Nick Cleaton’s solution manages to avoid it).
I had read about arithmetic coding before, but I never had any reason to sit down to implement it. It always struck me as kind of mystical: How the heck you encode information in a fraction of a bit, anyway? The 1MB Sorting Problem turned out to be a great excuse to learn how arithmetic coding works.
How Many Sorted Sequences Even Exist?
It’s important to note that the whole reason why we are able to represent a sorted sequence of one million 8-digit numbers in less than 1 MB of memory is because mathematically, there simply aren’t that many different sorted sequences which exist.
To see this, consider the following method of encoding a sorted sequence as a row of boxes, read from left to right.

An empty box tells us to increment the current value (initially 0), and a box with a dot inside it tells us to return the current value as part of the sorted sequence. For example, the above row of boxes corresponds to the sorted sequence { 3, 7, 7, 10, 15, 16, … }.
Now, to encode one million 8-digit numbers, we’d need exactly 1000000 boxes containing dots, plus a maximum of 99999999 empty boxes. In fact, when there are exactly 99999999 + 1000000 boxes in total, we can encode every possible sorted sequence using a unique distribution of dots. The question then becomes: How many different ways are there to distribute those dots? This is a straightforward number of combinationsproblem:
That’s a lot of combinations. Now, think of the contents of memory as one giant label which represents exactlyone of those combinations. The exponent on the 2, above, gives us a lower limit for how many bits of memory would be required to come up with a unique label for every possible combination. In this case, it can’t be done using fewer than 8093730 bits, or 1011717 bytes.
That’s the fundamental limit. No encoding scheme can ever do better than that; it would be like trying to uniquely label every state in the USA using fewer than 6 bits. On the bright side, 1011717 bytes is comfortably less than our 1048576 byte limit, which is encouraging.
The Probability of Encountering Each Delta Value
In the last post, we saw the potential of encoding delta values – the differences between numbers in a sorted sequence. Thinking in terms of the above rows of boxes, let’s take a look at the probability of encountering each delta value.
Since we know that there are 99999999 empty boxes, and 1000000 boxes containing dots, the probability of any particular box containing a dot is just:
For simplicity, let’s now imagine an infinite row of boxes, with dots occurring at the same frequency as this. The probability of encountering a delta value of 0 is, then, the same as the probability of a box containing a dot, which is just D.
How about a delta value of 1? Well, the probability of the first box being empty is (1 - D), while the probability of the second box containing a dot is still just D. Since each outcome is an independent event, we can multiply those probabilities together. The probability of encountering a delta value of 1, then, is
And in general, the probability encountering a delta value of N is
Now, let’s draw the real number line in the interval [0, 1), and let’s subdivide it into partitions according to the probabilities of each delta value. They begin quite small – you can see the first three partitions for delta values0, 1 and 2 squished all the way to the left – and they get infintessimally smaller as we proceed to the right, as larger delta values are exponentially less likely to occur.

If you were to throw a dart at this number line, the likelihood of hitting each partition is about the same as the likelihood of encountering each delta value in one of our sorted sequences.
That’s exactly the kind of information that’s useful for arithmetic coding.
The Idea Behind Arithmetic Encoding
Arithmetic encoding is able to encode a sequence of elements – in this case, delta values – by progressively subdividing the real number line into finer and finer partitions. At each step, the relative width of each partition is determined by the probability of encountering each element.
Suppose the first delta value in the sequence is 27. We begin by locating the corresponding partition in the original number line, and zooming into it. This gives us a new interval of the real number line to work with – in this case, roughly from .236 to .243 – which we can then subdivide further. Let’s use the same proportions we used for the first element.

Suppose the next element in the sequence is 39. Again, we locate the corresponding partition and zoom in, subdividing the interval into even finer partitions.
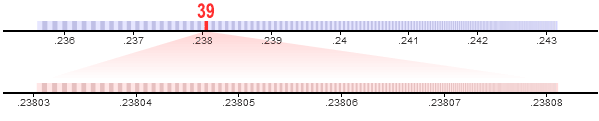
In this way, the interval gets progressively smaller and smaller. We repeat these steps one million times: once for each element in the sequence. After that, all we need to store is a single real value which lies somewhere within the final partition. This value will unambiguously identify the entire one-million-element sequence.
As you can imagine, to represent this value, it’s going to take a lot of precision. Hundreds of thousands times more precision than you’ll find in any single- or even double-precision floating-point value. What we need is a way to represent a fractional value having millions of significant digits. And in arithmetic coding, that’s exactly what the final encoded bit stream is. It’s one giant binary fraction having millions of binary digits, pinpointing a specific value somewhere within the interval [0, 1) with laser precision.

That’s great, you might be thinking, but how the heck do we even work with numbers that precise?
This post has already become quite long, so I’ll answer that question in a separate post. You don’t even have to wait, because it’s already published: See Arithmetic Encoding Using Fixed-Point Math for the thrilling conclusion!
以上内容来源:http://preshing.com/20121105/arithmetic-coding-and-the-1mb-sorting-problem/