杨辉三角(Pascal Triangle)的几种C语言实现及其复杂度分析

说明 

     本文给出杨辉三角的几种C语言实现，并简要分析典型方法的复杂度。

     本文假定读者具备二项式定理、排列组合、求和等方面的数学知识。

一  基本概念

     杨辉三角，又称贾宪三角、帕斯卡三角，是二项式系数在三角形中的一种几何排列。此处引用维基百科上的一张动态图以直观说明(原文链接http://zh.wikipedia.org/wiki/杨辉三角)：

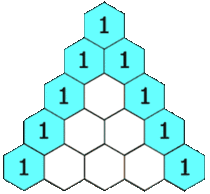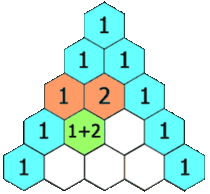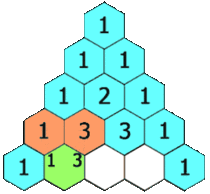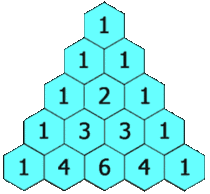
     从上图可看出杨辉三角的几个显著特征：

     1. 每行数值左右对称，且均为正整数。

     2. 行数递增时，列数亦递增。

     3. 除斜边上的1外，其余数值均等于其肩部两数之和。

     杨辉三角与二项式定理有密切关系，即杨辉三角的第n行(n=0…MAX_ROW)对应二项式(a+b)ⁿ展开(Binomial Expansion)的系数集合。例如，第二行的数值1-2-1为幂指数为2的二项式(a+b)²展开形式a² + 2ab + b²的系数，即。

     应用组合公式可推导出杨辉三角的特征1和3，如下：

 

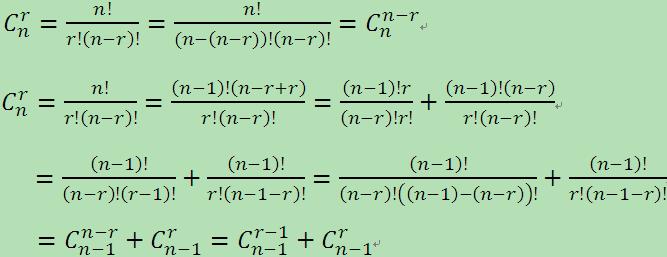
二  题目要求

     用C语言编程打印出MAX_ROW行杨辉三角数，如(MAX_ROW=5)：

1

1    1

1    2    1

1    3    3    1

1    4    6    4    1

1    5   10   10    5    1

…… …… …… ……

     并分析程序所用的加法和乘法次数，比较其复杂度。

三  算法实现

     因整型数值输出位宽限制，本节实现中将杨辉三角行数限制为10。该限制并不影响算法实现的完整性和表达性。

3.1 基本算法

     直接利用特征3求解杨辉值，即第i行的第j个数等于第i-1行的第j-1个数与第j个数之和，用二维数组形式表达即为a[i][j] = a[i-1][j-1] + a[i-1][j]。

     算法实现如下：

void BasicYangHui(void)
{
    int dwRow = 0, dwCol = 0, aTriVal[MAX_ROW][MAX_COL] = {{0}};

    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        aTriVal[dwRow][0] = aTriVal[dwRow][dwRow] = 1;  //若为i行0或i列，则i行j列杨辉值为1
    }

    for(dwRow = 2; dwRow < MAX_ROW; dwRow++)
    {
        for(dwCol = 1; dwCol < dwRow; dwCol++) //否则，i行j列杨辉值为i-1行中第j-1列与第j列值之和
            aTriVal[dwRow][dwCol] = aTriVal[dwRow-1][dwCol-1] + aTriVal[dwRow-1][dwCol];
    }

    //输出杨辉三角值
    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        for(dwCol = 0; dwCol <= dwRow; dwCol++)
        {
            printf("%5d", aTriVal[dwRow][dwCol]);
        }
        printf("
");
    }
}

     上述程序还可优化，利用对称性折半赋值以使加法计算减半。

void BasicYangHui2(void)
{
    int dwRow = 0, dwCol = 0, aTriVal[MAX_ROW][MAX_COL] = {{0}};

    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        aTriVal[dwRow][0] = aTriVal[dwRow][dwRow] = 1;  //若为i行0或i列，则i行j列杨辉值为1
    }

    for(dwRow = 2; dwRow < MAX_ROW; dwRow++)
    {
        for(dwCol = 1; dwCol <= dwRow/2; dwCol++)
            aTriVal[dwRow][dwCol] = aTriVal[dwRow-1][dwCol-1] + aTriVal[dwRow-1][dwCol];
        for(dwCol = dwRow-1; dwCol > dwRow/2; dwCol--) //此处必须取大于号，才能保证正确对折
            aTriVal[dwRow][dwCol] = aTriVal[dwRow][dwRow-dwCol];
    }

    //输出杨辉三角值
    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        for(dwCol = 0; dwCol <= dwRow; dwCol++)
        {
            printf("%5d", aTriVal[dwRow][dwCol]);
        }
        printf("
");
    }
}

     注意，BasicYangHui和BasicYangHui2均先计算杨辉值后统一打印输出。也可边计算边输出：

void BasicYangHui3(void)
{
    int dwRow = 0, dwCol = 0, aTriVal[MAX_ROW][MAX_COL] = {{0}};

    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        for(dwCol = 0; dwCol <= dwRow; dwCol++)
        {
            if((0 == dwCol) || (dwRow == dwCol))
                aTriVal[dwRow][dwCol] = 1;
            else
                aTriVal[dwRow][dwCol] = aTriVal[dwRow-1][dwCol-1] + aTriVal[dwRow-1][dwCol];
            
            printf("%5d", aTriVal[dwRow][dwCol]);
        }
        printf("
");
    }
}

3.2 递归算法

     利用特征3所对应的组合恒等式，可方便地写出杨辉三角的递归算法。

//求杨辉三角中第i行第j列的值
int CalcTriVal(int dwRow, int dwCol)
{
    if((0 == dwCol) || (dwRow == dwCol))
        return 1;
    else
        return CalcTriVal(dwRow-1, dwCol-1) + CalcTriVal(dwRow-1, dwCol);
}

void RecursiveYangHui(void)
{
    int dwRow = 0, dwCol = 0;

    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        for(dwCol = 0; dwCol <= dwRow; dwCol++)
        {
            printf("%5d", CalcTriVal(dwRow, dwCol));
        }
        printf("
");
    }
}

3.3 迭代算法

     通过组合公式推导，可得等效的迭代表达dwTriVal = dwTriVal * (dwRow-dwCol) / (dwCol+1)。

     相应的算法实现如下：

void BinomialYangHui(void)
{
    int dwRow = 0, dwCol = 0, dwTriVal;

    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {   //首列直接输出1，否则由二项式系数递推公式求出杨辉值
        dwTriVal = 1;
        for(dwCol = 0; dwCol <= dwRow; dwCol++)
        {
            printf("%5d",dwTriVal);
            dwTriVal = dwTriVal * (dwRow-dwCol) / (dwCol+1);
        }
        printf("
");
    }
}

3.4 覆盖算法

     本节将用一维数组代替二维数组，并结合对称性(“折半”)，使加法次数和存储空间减半。其示意图如下所示：

 

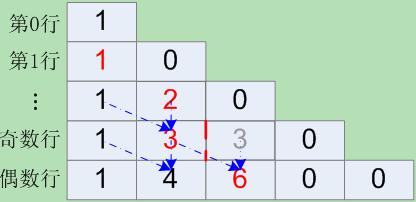
     图中红色数字为折半边界，同列数字对应一维数组的同一存储位置。数组顺序存储单行杨辉值，只计算边界以左的杨辉值，每次计算后用新行值覆盖前行值。为便于说明，将前行col列值记为a[col]，新行col列值记为a’[col]，注意a[col]和a’[col]实际上对应同一存储位置。

     可见，计算奇数行(行数从0开始)首列边界处的杨辉值a’[col]时，可将a[col]与a[col-1]值相加后赋值给a’[col]；计算偶数行首列边界处的杨辉值a’[col]时，因a[col]位于折半边界以右(其值为0)，需将a[col-1]赋予a[col]再与a[col-1]值相加后赋值给a’[col]。自边界处向左依次计算至第1列(0列直接置1)，然后正向输出存储的杨辉值(对应边界以左值)，再反向输出所存值(对应边界以右值)。继续以上步骤处理下一行。

     考虑到偶数行相对前行边界右移一位，故数组空间大小定义为(MAX_ROW+1)/2。

     算法实现如下。注意，计算row行数据时，数组预存的是row-1行数据。

void EfficientYangHui(void)
{
    int dwRow = 0, dwCol = 0, aTriVal[(MAX_ROW+1)/2] = {1};
    printf("%5d
", aTriVal[0]); //先输出首行杨辉值，以便后面各行可采用统一的算法

    for(dwRow = 1; dwRow < MAX_ROW; dwRow++)
    {
        if(0 == (dwRow % 2)) //偶数行折半处为元素自加，如1-3-0-0为1+3、3+3(而非3+0)
            aTriVal[dwRow/2] = aTriVal[dwRow/2-1];
        for(dwCol = dwRow/2; dwCol >= 1; dwCol--)
        {
            aTriVal[dwCol] = aTriVal[dwCol] + aTriVal[dwCol-1];
        }
        aTriVal[0] = 1; //首列置1

        for(dwCol = 0; dwCol <= dwRow/2; dwCol++)
        {
            printf("%5d", aTriVal[dwCol]); //并输出aTriVal[dwCol]作为前半行杨辉值
        }
        for(dwCol = (dwRow-1)/2; dwCol >= 0; dwCol--)
        {
            printf("%5d", aTriVal[dwCol]); //反向输出aTriVal[dwCol]，构成后半行杨辉值
        }
        printf("
");
    }
}

     以下给出另一种覆盖算法。该算法未使用折半处理，但使用临时变量暂存待覆盖的右肩值(即示意图中前行同列值)，并从首列开始从左至右计算并覆盖。

void EfficientYangHui2(void)
{
    int dwRow = 0, dwCol = 0, dwLeft = 0, dwRight = 0;
    int aTriVal[MAX_ROW+1] = {1};

    for(dwRow = 0; dwRow < MAX_ROW; dwRow++)
    {
        dwLeft = 0;
        for(dwCol = 0; dwCol <= dwRow; dwCol++)
        {
            dwRight = aTriVal[dwCol];
            aTriVal[dwCol] = dwLeft + dwRight;
            dwLeft = dwRight;
            printf("%5d", aTriVal[dwCol]);
        }
        printf("
");
    }
}

四  复杂度分析

     不同于传统定义的时间复杂度计算，本节将时间复杂度等同于循环体内杨辉值加减乘除运算的次数，即侧重运算效率。基于相应的算法思想，可方便地改编为符合传统时间复杂度期望的实现。

     此外，本节将空间复杂度等同于存储杨辉值的数组大小。因代码中已加以体现，此处不再分析。

     将杨辉三角总行数记为N(亦即MAX_ROW)，本节计算BasicYangHui、RecursiveYangHui和BinomialYangHui三种典型算法的时间复杂度。计算主要用到以下公式：

4.1 BasicYangHui复杂度

     主要计算BasicYangHui函数内层循环中加法运算(13行)的执行次数。

     可知，每行杨辉值需要执行dwRow - 1次加法运算。通过求和公式推导总的加法次数为

 

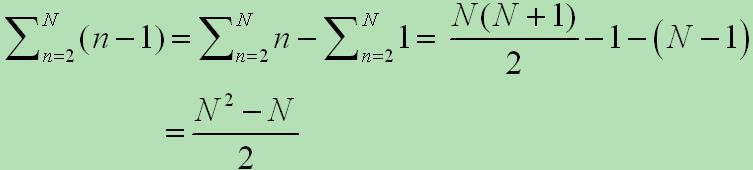
4.2 RecursiveYangHui复杂度

     递归算法的时间复杂度计算稍微复杂，以下借助二项式定理进行推导。

     对于(a+b)ⁿ，其展开式第r项的系数满足：。

     由此结合递归算法，可得：

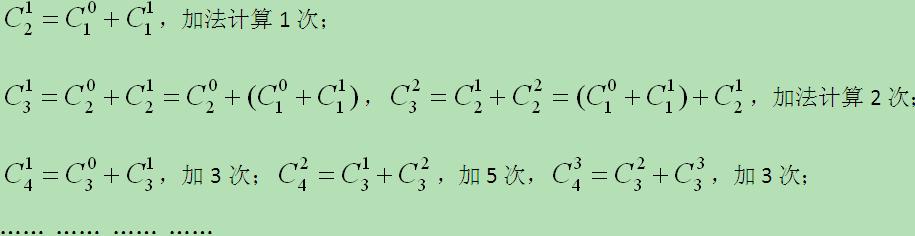
     以此类推，将各个杨辉值对应的计算次数写成如下形式：

0

0        0

0        1         0

0        2         2         0

0        3         5         3        0

0        4         9         9        4         0

0        5         14       19       14       5         0

……  ……  ……  ……

     可看出所形成的新三角相当于杨辉三角每个元素减1而成。

     根据二项式系数和公式，可知每行元素和(加法次数)为

     求和得总的加法次数为

 

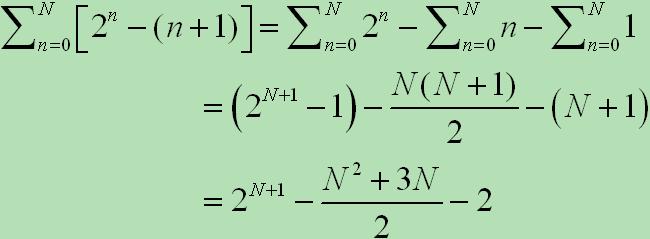
     可见RecursiveYangHui中采用递归调用算法时间复杂度很高。递归代码在紧凑易懂的同时，牺牲了执行速度(实际上因为大量使用堆栈内存也牺牲了空间)。

4.3 BinomialYangHui复杂度

     主要计算BinomialYangHui函数内层循环中dwTriVal * (dwRow-dwCol) / (dwCol+1)句的运算次数。将其计为一次乘法、一次减法和一次除法(加1运算不计)，共三次运算。

     可知，每行杨辉值需要执行(dwRow + 1) * 3次运算。通过求和公式推导总的运算次数为

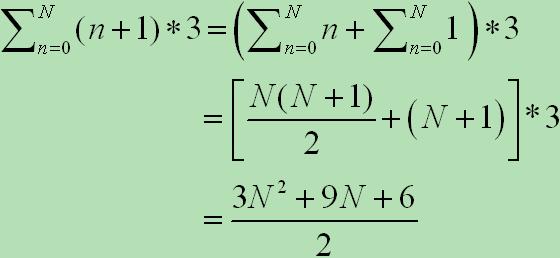
五  总结

     对比BasicYangHui、RecursiveYangHui和BinomialYangHui三种算法的复杂度可知：

• Ÿ时间复杂度：BasicYangHui最低，RecursiveYangHui最高(达到指数级)；
• Ÿ空间复杂度：BinomialYangHui最低，BasicYangHui较高。RecursiveYangHui因消耗大量栈空间故复杂度也较高。 

如果，您认为阅读这篇博客让您有些收获，不妨点击一下右下角的【推荐】。
如果，您希望更容易地发现我的新博客，不妨点击一下左下角的【+加关注】。
如果，您对我的博客所讲述的内容有兴趣，请继续关注我的后续博客，我是【clover_toeic】。
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。