学习来源:计蒜客
1.图的基础东西http://blog.csdn.net/u012763794/article/details/51103766
2.图的遍历是什么
什么是图的遍历呢?从图的某个顶点出发,沿图中的路径依次访问图中所有顶点,并且使得图中所有顶点都恰好被访问一次,这一过程即为图的遍历。需要注意的是,接下来讨论图的遍历时,都是特指在一个连通图上进行遍历。(你不连通我怎么遍历)
图有两种最常见的遍历算法:广度优先搜索(Breadth-First-Search,BFS)和深度优先搜索(Depth-First-Search,DFS)
简单来说广度优先是一层一层地向外扩展,深度优先是一个劲地往下走
3.广度优先搜索
注:下面的是无向图
#include <iostream>
#include <vector>
#include <cstring>
#include <queue>
using namespace std;
class Graph{
private:
int n; //顶点个数
bool *visited; //数组,用于标记对应编号的点是否已经被访问过了,
vector<int> *edges; //邻接表
public:
Graph(int input_n){
n = input_n;
edges = new vector<int>[n];
visited = new bool[n];
memset(visited, 0, n);
}
~Graph(){
delete[] edges;
delete[] visited;
}
//插入,这里我们是当他是无向图,所以两边都一样插入到各自的邻接表中
void insert(int x, int y){
edges[x].push_back(y);
edges[y].push_back(x);
}
//start_vertex:遍历的起点
void bfs(int start_vertex){
//声明一个int型的队列
queue<int> bfs_queue;
//将起点加入队列,并设置为已访问
bfs_queue.push(start_vertex);
visited[start_vertex] = true;
//队列为空停止循环
while (!bfs_queue.empty()) {
//获取队首元素的编号,并输出
int vertex = bfs_queue.front();
cout<<vertex<<endl;
//将其从队列删除
bfs_queue.pop();
//寻找vertex相邻的所以顶点,没被访问的就设置为已访问,并加加入队列,
for (vector<int>::iterator it = edges[vertex].begin(); it != edges[vertex].end(); it++ ) {
if (!visited[*it]) {
visited[*it] = true;
bfs_queue.push(*it);
}
}
}
}
};
int main(){
int n, m, k;
cout<<"请分别输入顶点数和边数"<<endl;
cin >> n >> m;
Graph g(n);
cout<<"请分别输入无向边"<<endl;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
g.insert(x, y);
}
cout<<"请输入遍历的起点"<<endl;
cin >> k;
g.bfs(k);
}运行结果:
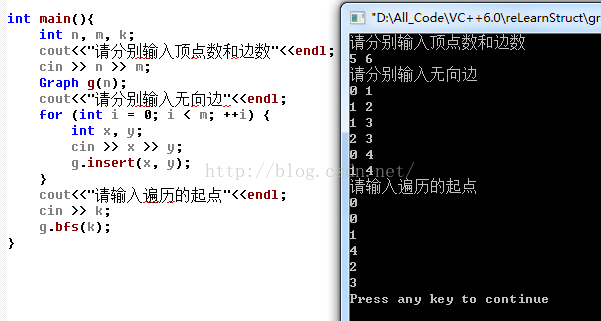
4.深度优先搜索
遍历一般是无向图
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
class Graph{
private:
int n; //顶点数量
vector<int> *edges; //邻接表
bool *visited; //记录结点是否已经访问过了
public:
Graph(int input_n){
n = input_n;
edges = new vector<int>[n];
//初始化visited指针
visited = new bool[n];
memset(visited, 0, n);
}
~Graph(){
delete[] edges;
delete[] visited;
}
void insert(int x, int y){
edges[x].push_back(y);
edges[y].push_back(x);
}
//vertex:起点的编号
void dfs(int vertex){
cout<<vertex<<endl;
visited[vertex] = true; //标记为已访问
//c++11可以写成下面的这一句
//for (int adj_vertex:edges[vertex]) {
for (vector<int>::iterator it = edges[vertex].begin(); it != edges[vertex].end(); it++ ) {
//遍历跟起点相邻的顶点,没被访问过就递归调用深度优先搜索
if (!visited[*it]) {
dfs(*it);
}
}
}
};
int main(){
int n, m, k;
cout<<"请分别输入顶点数和边数"<<endl;
cin >> n >> m;
Graph g(n);
cout<<"请分别输入无向边"<<endl;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
g.insert(x, y);
}
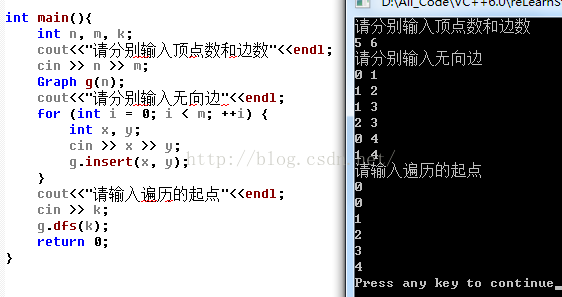
cout<<"请输入遍历的起点"<<endl;
cin >> k;
g.dfs(k);
return 0;
}
运行结果: