1. 传统的方法
1.1 相似检索(特征提取,相似度计算)
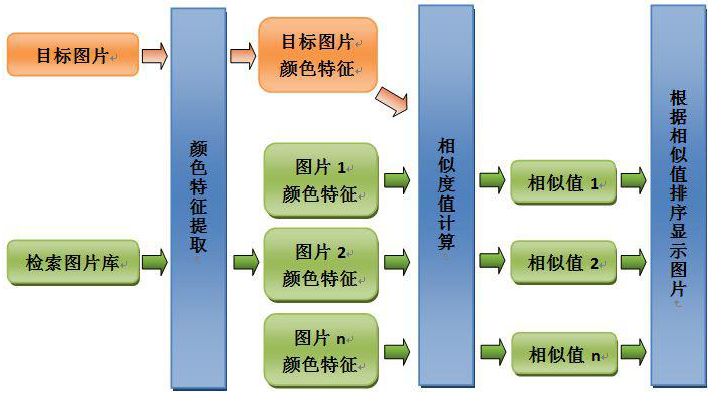
技术框架:

算法结构:
目标:实现基于人类颜色感知的相似排序
主要模块:颜色特征提出;特征相似度计算
1.1.1 颜色、纹理、形状
a. 相似颜色检索
统计RGB图像中颜色,形成直方图,转化为向量。这种固定维度直方图维度太高,可以用自编码器降维。自编码器是通过神经网络提取针对样本的通用特征的降维方法,隐藏层的维数小于输入样本的维数,最后还需要升维使隐藏层的输出最大限度的保存图像的主要特征,以使还原后的图像与原图像误差达到最小。
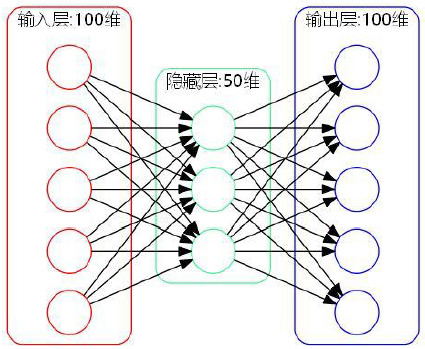
也可以用聚类直方图统计图像的颜色成份,使唤K-means++对图片Lab像素进行聚类 横轴的颜色维数会减少。
相似度计算:色差距离(CIEDE200)
颜色差异多少算是有差距的。色差容忍度(Tolerance),感知均匀的色差距离,色差小于Just-Noticeable-Difference阈值,人类视觉对绿色差异不敏感,对蓝色差异比较敏感,(不均匀)。CIE1931颜色空间 从人眼色差容忍度来计算差异(Delta E_{ab}^*=sqrt{(L_2^*-L_1^*)^2+(a_2^*-a_1^*)^2+(b_2^*-b_1^*)^2}),容忍椭圆,非感知均匀
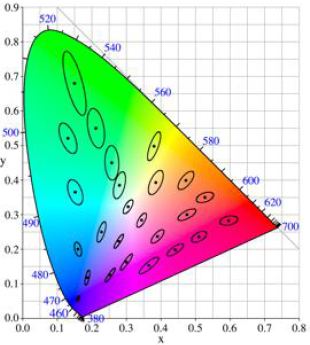
CIELab颜色空间, 视觉感知均匀的颜色模型。 CIEDE2000,均匀性更好的距离(Delta E_{00}^{12}=Delta E_{00}(L_1^*,a_1^*,b_1^*; L_2^*, a_2^*, b_2^*)=sqrt{left(frac{Delta L^prime}{k_LS_L}
ight)^2+left(frac{Delta C^prime}{k_CS_C}
ight)^2+left(frac{Delta H^prime}{k_HS_H}
ight)^2+R^Tleft(frac{Delta C^prime}{k_CS_C}
ight)left(frac{Delta H^prime}{k_HS_H}
ight)})
相似度计算:颜色直方图距离(Earth Mover Distance 推土机距离 Wasserstein 距离)
两个图片的颜色特征直方图之间的视觉相似度作为检索结果的排序依据
EMD是两个多维特征分布之间的非相似性度量,是一个传统运输分配问题。
场景属于多对多分配,比如物资运送,多个供应商对多个需求客户;土堆搬运,多个土堆对多个土坑;约束条件是要求双方的节点总量相等,不同节点之间的成本不同;目标是分配的成本最小。比如多个土堆的量正好能填满多个土坑;土坑在不同的位置,土堆在不同的位置;最近的土堆推到最近的土坑,如果多出来的土,或者不满的坑,都从最近的位置去寻找解决
假定:有三个土堆的土量都是5个单位;三个土坑所能容纳的土量分别是3、7、5;不同的土堆和土坑之间的距离不同,分别是1、2、3,最近的为1,最远的为3;有一个搬运工,一趟只能搬运1单位的土
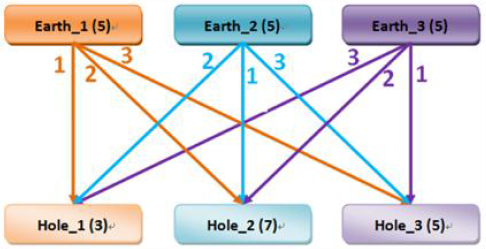
目标:以最小的行走距离EMD,将所有的土堆运输到土坑并填平
解:贪心法。先往自己最近的坑推。于是Hole_1, Hole_3先平,Earth_1多出来的部分只能稍远一点
计算EMD距离:(3 imes 1+2 imes 2+5 imes 1+5 imes 1=17)
顺序 E1->H1:3; E1->H2:2; E2->H2:5; E3->H3:5.
场景:颜色特征直方图
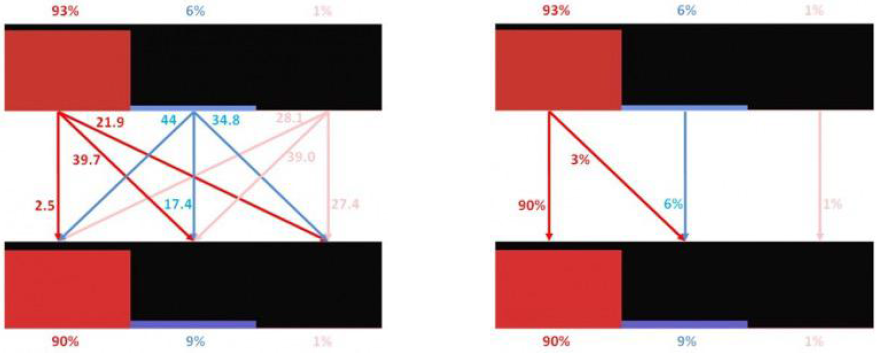
计算EMD距离:(2.5 imes 90\%+39.7 imes3\%+17.4 imes 6\%+27.4 imes 1\%=4.795)
其中2.5, 39.7等颜色距离权重是CIEDE2000距离。
思路: 对图库里的图片算颜色直方图(特征提取),对搜索图片计算颜色直方图(特征提取),然后计算EMD距离,对距离值排序,值比较小的是最接近的图片。
b. 相似纹理检索
纹理是图像中的重复模式:元素或基元按一定规则排序。纹理特征:反映图像中同质现象的视觉特征。
算法结构:目标是实现基于人类纹理感知的相似排序。先特征提取再做相似度计算。
纹理特征提取。特征空间:多方向、多尺度Gabor滤波器组。特征计算:Kmeans++聚类直方图。
Gabor滤波器组:类似于人类的生物视觉系统,多频率多尺度多方向。
频域:属于加窗傅立叶变换。空域:一个高斯核函数和正弦平面波的乘积。
复数:(g(x,y;lambda, heta,psi,sigma,gamma)=expleft(-frac{x^{prime2}+gamma^2y^2}{2sigma^2}
ight)expleft(ileft(2pifrac{x^prime}{lambda}+psi
ight)
ight))
实部:(g(x,y;lambda, heta,psi,sigma,gamma)=expleft(-frac{x^{prime2}+gamma^2y^2}{2sigma^2}
ight)cosleft(2pifrac{x^prime}{lambda}+psi
ight))
虚部:(g(x,y;lambda, heta,psi,sigma,gamma)=expleft(-frac{x^{prime2}+gamma^2y^2}{2sigma^2}
ight)sinleft(2pifrac{x^prime}{lambda}+psi
ight))
其中:(x^prime=xcos heta+ysin heta), (y^prime=-xsin heta+ycos heta)
例如Gabor滤波器:6频率(尺度)8方向;频率:1,2,3,4,5,6;尺寸:25,35,49,69,97,137;方向:0,22.5,45,67.5,90,112.5,135,157.5。

特征提取步骤:
- 彩色图片灰度化
- 提取灰度图的Gabor滤波器特征(减小原图尺寸和卷积使用快速傅立叶变换的方法来提高计算速度)
- 6频率(尺度)、8方向的Gabor
- 48个同尺寸的特征图
- 每个像素对应48维的Gabor向量
- 使用Kmeans++聚类所有像素Gabor特征
- K根据数据集纹理复杂度而定
- 使用KD-tree加速
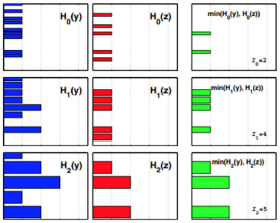
示例K=10:

特征相似度计算
纹理聚类直方图:EMD;纹理距离:L2
c. 相似形状检索
PHOG形状特征提取:
HOG直方图方向数量:9
梯度方向直方图金字塔:(1 imes1), (2 imes2), (4 imes4);维数(1 imes1 imes9+2 imes2 imes9+4 imes4 imes9=189)
使用灰度图后进行分块,采用Sobel梯度图或者Canny边缘图等得到每一块的直方图,对这些直方图级联拼到一块得到PHOG的特征向量.
缺点:只检验图形轮廓是否大体一致,比HOG的结果要粗糙。比如只有图像是正着存储的效果会好点,比如图片里的人需要都是站立的等等。
特征相似度计算:
标准化欧氏距离:
(S_i 为样本集特征中每一维对应的标准差)
(Dist(P,Q)=sqrt{sumlimits_ileft(frac{P_i-Q_i}{S_i}
ight)^2})
直方图相交(Histogram Intersection):
(Sim(P,Q)=sumlimits_{i=1}^{i=n}min(P_i,Q_i))
1.1.2 局部特征点
a. 相似局部特征检索
特征提取:
检测出所有的局部特征点和特征描述子

(4 imes4 个8方向梯度方向直方图=128维描述子)
比如SIFT特征点,SIFT特征点有很多改变的形式比如SURF,Color-SIFT颜色层面,Affine-SIFT基本上是类似于线性的扭曲变形,Dense-SIFT把SIFT像HOG一样进行叠起来,两个图片相互叠着,PCA-SIFT先用PCA降维再用SIFT。
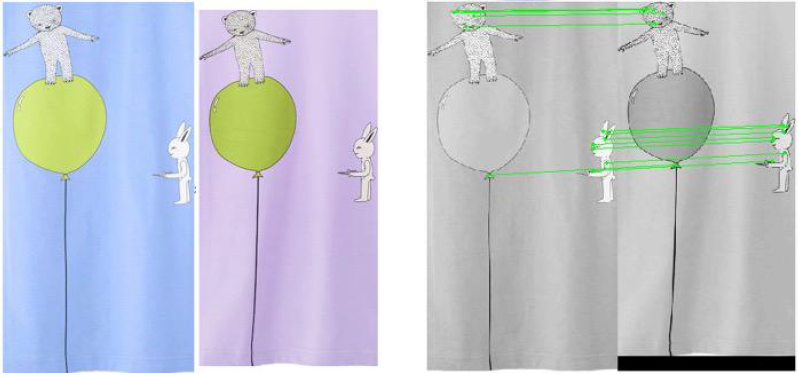
相似度计算:计算两个图SIFT点集之间匹配的有多少对
b. 词包 Bag Of Visual Word
图片形式的词包。借用自然语言处理里的方法。BoW model 忽略文本的语法和语序,用一组无序的单词word来表达一段文字或一个文档。

视觉的词包 Bag of Visual Word
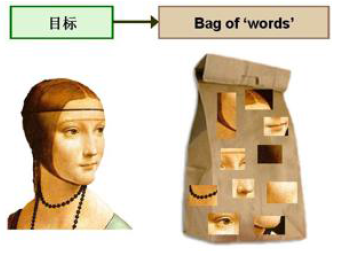
将一些某一类图片的共有特征作为词汇组件,比如人脸图片的眼睛、鼻子等,自行车图片的车轮、脚踏板等,并形成向量。
-
假定训练集有M幅图像,对训练集进行预处理,包括图像增强、分割、统一格式、统一规格等。
-
对每一幅图像(将图像打成小的patch,对每个patch提取SIFT特征)提取若干个SIFT特征(每幅图像的SIFT特征数量不一样)。每个特征是128维的描述子矢量。


-
对所有图像的所有描述子特征矢量进行Kmeans聚类。设定K个聚类中心。给聚类中心取个名字叫视觉词。
-
对每个图像的每一个SIFT特征与k个聚类中心(视觉词,这个集合即为视觉词字典)计算距离(L1、L2),每个SIFT特征与最近的视觉词(聚类中心)就认为该SIFT特征是该视觉词,也认为该图像包含一个这个视觉词,每个图像的SIFT特征与某个视觉词最近的情况都统计起来,则在文本中即为该文本包含该单词多少次即词频,文本出现某个单词的次数,同样图像也可以统计出现视觉词的次数,有了视觉词频就可以画直方图(图像中k个视觉词出现的词频),也有了向量,即k维向量。这样类似文本,图像就可以用K维向量来表示。

2. 基于深度学习DL的方法
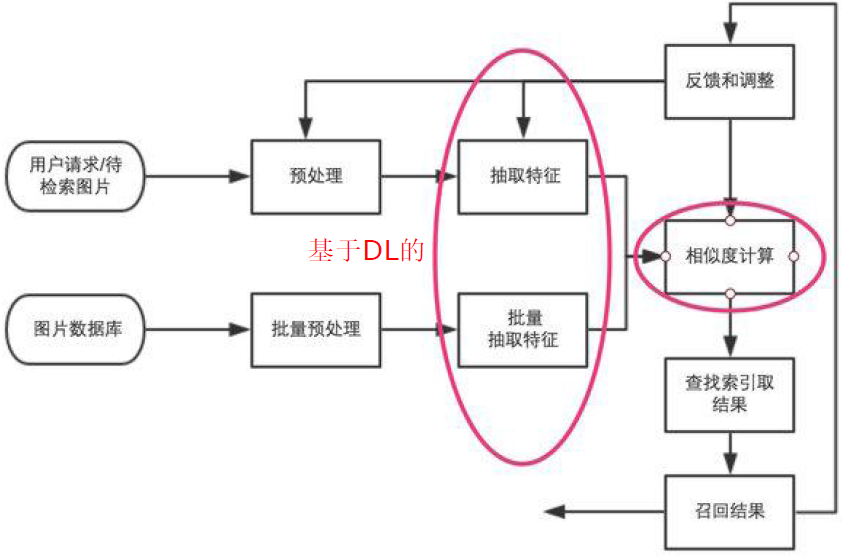
2.1 迁移学习(特征提取)
迁移学习可以使用VGG16这样成熟的物品分类的网络,只训练最后的softmax层,只需要几千张图片,使用普通的CPU就可以完成,而且模型的准确性不错。
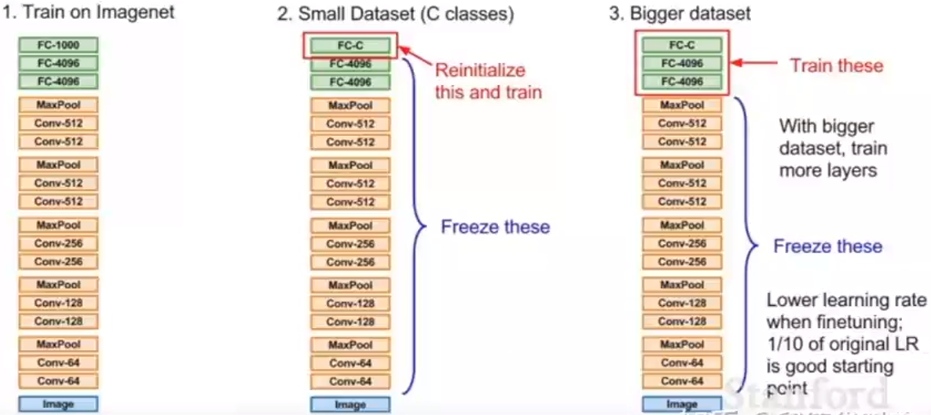
迁移学习思想:迁移学习假定不同的数据集之间,初级特征比如折线、边角等都是相同的,因此不需要再重新训练这些参数,直接使用就行。
迁移实现思路:将前面的网络的层的学习率设置很小的值接近于0((etaapprox 0) 权重不更新(mathrm{w}(m+1)=mathrm{w}(m)+Deltamathrm{w}(m)=mathrm{w}(m)-etafrac{partial J}{partial mathrm{w}})), 只学习后面的层。如果数据集小,只训练最后一层。如果数据集大,多训练几层。
2.2 基于深度学习的二值哈希编码
特征提取:
在ImageNet中的卷积神经网络结构(如 AlexNet 5个卷积层和3个全连接层)基础上在第7层(4096个神经元)与output层之间加一个隐层(全连接层)。这一层的激活函数使用 sigmoid 输出值在0-1之间,设定阈值(比如0.5)将输出二值化,并使用这一层降低维度(比如使用128维),将这一层输出的01二值向量作为二值检索向量。在卷积神经网络的图像分类训练过程中,第7层输出4096维的最接近分类结果的特征向量被降低维度和二值化为低维度的01向量。这种降维和二值操作表征图像丰富(第7层4096维)。

加了一层之后,不再重新对整个网络做训练,而是用迁移学习的思路,复用ImageNet中得到的最终模型的前7层的权重,在此基础上做fine-tuning微调,相当于前面的7层保持不变(学习率(etaapprox0)),只训练后面的第7层、第8层(新加的)、output层之间的权重。这样新加的层能够比较好的代表第7层所体现的特征。新加的层的输出可以作为检索的索引。最后一层output层输出的是标签,倒数第二层即第8层(新加的)输出的01二值检索向量基本上表示一类图片,基本上相当于这一类图片的检索索引。

待检索的图片获得二值检索向量后,通过hash检索,找到对应的类二值检索索引,再对这一类的所有图片对比第7层的4096维向量,计算距离,重新对距离排序得到检索结果。
相较于传统的方法结合颜色、纹理、形状、关键点等,而且结合的过程中还要考虑每一种特征的权重,深度学习还是能够相当于端到端的解决问题。
3. 检索方法
在图像检索中,数据是海量和高维的,要快速地找到与某个数据最相似(距离最近)的数据或多个数据,可以使用类似索引的技术。最近邻查找 Nearest Neighbor 如 K-dimensional tree, 近似最近邻查找 Approximate Nearest Neighbor,如Locality Sensitive Hash
3.1 Kd-tree
多维度查询方法。一种用于多维度检索的二叉平衡树.
构建Kd-tree
- 输入: N 个 d 维的数据点,以2 个维度为例(x,y):(2,3),(5,4),(4,7),(9,6),(7,2),(8,1)
- 确定split 值:方差最大的维度, 如 x
- 在确定的split值所在的维度上的中值点(7, 2)作为节点,首次进行算法时为根节点
- 确定左右子树
- 左子树:split 维度上小于节点 (2,3),(5,4),(4,7)
- 右子树:split 维度上大于节点 (8,1),(9,6)
- 对左右子树分别循环以上步骤
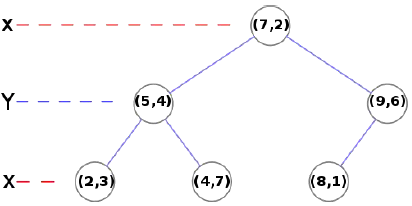
最近邻查找
类似二叉树搜索,从根结点,根据构建过程中split所在维度进行比较,对左右子树进行查询,查到叶子节点后,回溯检查另一半子空间是否有更近的点(欧氏距离)
路径: (7,2)->(5,4)->(4,7)
回溯: (5,4)->(2,3)
3.2 局部敏感哈希 Locality Sensitive Hash
处理海量高维数据。2个相似度很高的数据以较大概率映射成同一个hash值,2个相似度低的数据以极低的概率映射成同一个hash值。传统的哈希算法可能2个相近的数的hash后分到比较远的桶,如使用hash函数(Hash(x)=x\% 8), (Hash(255)=255\% 8 =7), (Hash(257)=257\% 8=1), (Hash(1023)=1023\% 8=7), 255与257的hash值比较远,255与1023的hash值比较近。要使得原始空间上分布离的近数hash后也能够的近一点的hash桶,在哈希空间上分布的近一点,也即选用局部敏感哈希的函数。
将这一族 满足以下条件的 hash 函数 (H={h:S ightarrow U}) 称为是((r_1,r_2,p_1,p_2))敏感的。
如果 两人个数据的差异程度或者距离 (d(O_1,O_2)lt r_1), 那么(O_1), (O_2) 分到一个桶或者相近的桶的概率 (Pr[h(O_1)=h(O_2)]geq p_1)。即两个足够相似的数据,映射为同一hash值的概率足够大。
如果 差异程度或者距离 (d(O_1,O_2)gt r_2), 那么(O_1), (O_2) 分到一个桶或者相近的桶的概率 (Pr[h(O_1)=h(O_2)]leq p_2)。即两个足够不相似的数据,映射为同一hash值的概率足够小。
p-稳定分布
一个实数集(mathrm{R})上的分布(mathrm{D}),如果存在(pgeq 0), 对任何 (n)个实数 (v_1,cdots,v_n)(比如输入图像特征的向量)和(n)个满足(mathrm{D})分布的变量(X_1,cdots,X_n), 随机变量 (sum_i v_i X_i) (向量点乘,结果是一个数) 和 (sqrt[p]{sum_imid v_imid^p}X) ((p)(阶)范数,结果是一个数)有相同的分布,其中(X) 是服从(mathrm{D}) 分布的一个随机变量, 则称 (mathrm{D}) 为一个 p-稳定分布。
(p=1) 是柯西分布。 (p=2) 为二阶范数,(mathrm{D})是高斯分布。
p-稳定分布 使得可以估计给定向量在欧式空间下的(p)范数的长度 (parallel vparallel_p)。对于 (sqrt[p]{sum_imid v_imid^p}X) 不好计算,依据 p-稳定分布,(sqrt[p]{sum_imid v_imid^p}X) 与 (sum_i v_i X_i) 同分布,可以用计算 (sum_i v_i X_i) 来代替(sqrt[p]{sum_imid v_imid^p}X)。
对于 (p=2) 为二阶范数,(mathrm{D})是高斯分布。 所以取满足正态分布的一个数列,与某个图像特征的向量做向量点乘,得到一个数值,这个数值与这个图像特征的向量本身的2阶范数(即向量元素绝对值的平方和再开方,代表向量的长度,也是一个数值), 有同分布的性质。
假设有两个图像特征的向量 (mathbf{v1}), (mathbf{v2}), 用这两个特征分别与同一个正态分布的数列做向量点乘,所得到的2个数值在一维上的距离与 (mathbf{v1}), (mathbf{v2}) 在多维上的欧氏距离是同分布的。
选取p-stable Locality Sensitive Hash函数
(h_{mathbf{a},b}(mathbf{v})=lfloorfrac{mathbf{a}cdotmathbf{v}+b}{r}
floor): (mathcal{R}^d
ightarrowmathcal{N})
把 (d) 维向量 (mathbf{v}) 映射成为一条直线上的一个整数值。
在 p-stable 分布上独立、随机选取 (d) 维向量 (mathbf{a})。映射到直线上的分段长度 (r) (桶宽),在 ([0,r]) 上均匀随机选取偏移 (b)。对于 ((mathbf{v1}, mathbf{v2})) 投射距离 ((mathbf{a}cdot mathbf{v1}-mathbf{a}cdot mathbf{v2})) 与 (parallel mathbf{v1}-mathbf{v2}parallel_p X) 同分布,也即映射后远近程度与映射前的远近程度一样,映射后的距离与映射前的距离一样。
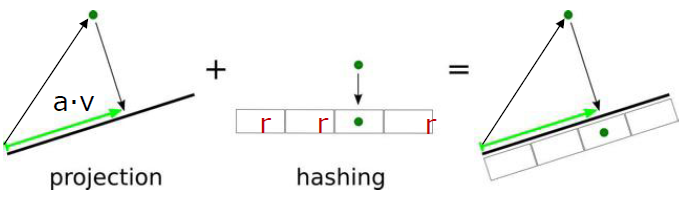
构建索引
由于是概率问题,还是有可能相似的数据不能投放到一个hash桶中,解决方法是用多个hash函数对向量进行hash运算。比如一个图像特征的向量 (mathbf{v_i}), 从LSH函数族中选取 (k) 个 hash 函数 (h_1(), h_2(),cdots, h_k()) 计算 (k) 个 hash 值 (h_1(mathbf{v_i}), h_2(mathbf{v_i}),cdots, h_k(mathbf{v_i}))。在查询的时候同样对查询向量 (mathbf{q}) 用同样的 (k) 个函数计算 (h_1(mathbf{q}), h_2(mathbf{q}),cdots, h_k(mathbf{q}))。 这两组值之间只有一个对应位的值相等,就认为 (mathbf{v_i}) 是查询 (mathbf{q}) 的一个近邻。
实现:
- 对于 (k) 个具有 ((r_1,r_2,p_1,p_2)) 局部敏感性的哈希原子函数 表示为函数 (mathcal{G}={g: S ightarrow U^k}) 即 (g(mathbf{v})=(h_1(mathbf{v}), h_2(mathbf{v}),cdots, h_k(mathbf{v}))), (h_iin H)。
- 从 (mathcal{G}) 独立、随机选取 (L) 个 LSH 函数 (g_1,cdots,g_L)。
- 构建 (L) 个 LSH 的索引表,为所有数据点计算 (g_i(mathbf{v})), (i=1,cdots, L) 对于数据集中任意一点(mathbf{v}),将其存储到桶(g_i(mathbf{v}))中
- 计算查询的 (L) 个LSH值 (g_1(mathbf{q}), cdots, g_L(mathbf{q})), 并在桶中搜索
工程中实际使用的方法:
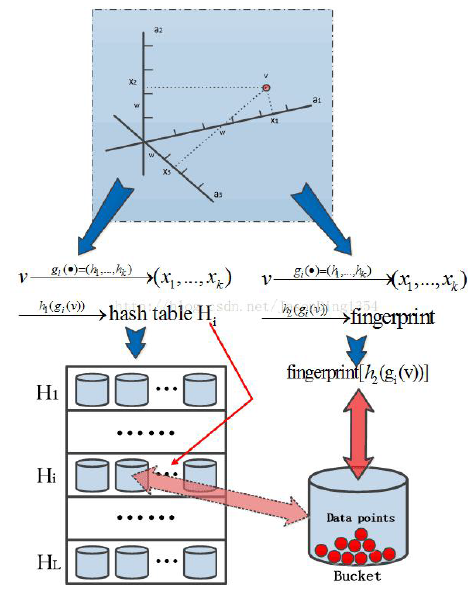
每个向量 (mathbf{v}) 经过 (g(mathbf{v})=(h_1(mathbf{v}), h_2(mathbf{v}),cdots, h_k(mathbf{v}))) 生成 (x_1,cdots,x_k)
构建索引表使用大素数 (C)。
(H_1(x_1,cdots,x_k)=(sumlimits_{i=1}^k r_ix_i mod C)mod size) 对表size 做 mod, 映射到某个桶里面,
(H_2(x_1,cdots,x_k)=(sumlimits_{i=1}^k r^prime_ix_i mod C)) 使用一个hash 函数将 ((x_1,cdots,x_k))计算一个哈希值作为指纹。
[1] https://towardsdatascience.com/understanding-locality-sensitive-hashing-49f6d1f6134
[2] https://blog.csdn.net/JasonDing1354/article/details/38227085
[3] https://www.cnblogs.com/hxsyl/p/4627477.html