
Solution:
这题可以分为两个部分,
一个部分为处理出每个点最大的金条数与最小的金条数,记为 ([Min_i, Max_i])
第二部分为对于 (n) 个变量 (x_iin[Min_i, Max_i]cup mathbb {Z}),计算选出 (B) 个前 (A) 大变量的方案数。
对于两个点 u->v ,如果有 u 的人 i (有金条) 与 v 的人 j 满足 (iequiv j( ext{mod }gcd(S_u, S_v))) ,那么 i 就可以给 j 假金条。
同理,对于一条路径 u->...->v 设 g 为其 (gcd) ,那么只要满足 (i equiv j( ext{mod }g)) ,那么 i 就可以给 j 假金条。
所以对于一个强连通分量中,有金条的人就会满足 (iequiv j( ext{mod } g)) ,j 为每个点有金条的人,g为整个强连通分量的 (gcd) 。
枚举一个点有金条的人,这样就可以 (O( ext{金条数目})) 求出每一个强连通分量的金条拥有状态。
由竞赛图的性质,缩点后的竞赛图还是竞赛图,而且会长这个样子:
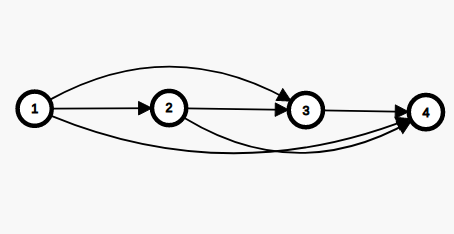
即每个点都向它后面连边,显然我们为了让金条数量最大化就是按照拓扑序依次算点的贡献,这样算出来每个强连通分量的金条数假设为 Mx 那么每个点u拥有的金条数就是(frac{S_uMx}{g})。
接下来就考虑怎么计数,为了不算重,枚举 u 为B中最小的点,然后统计出 (Max_u<Min_i) 的数量 (cnt_1),以及 (Max_igeq Max_ugeq Min_i) 的数量 (cnt_2),那么再枚举在 (cnt_2)个中选j个,给答案加上 ({~cnt_2~choose j}{~cnt_1~choose B - 1 - j})。
#include <iostream>
#include <cstdio>
#include <set>
#include <algorithm>
#include <vector>
#define LL long long
using namespace std;
const int maxn = 5003;
const int MOD = 1e9 + 7;
vector<int> g[maxn];
vector<bool> city[maxn];
int A, B, n;
int s[maxn], fac[maxn], ifac[maxn];
void input() {
char str[(int)(2e6) + 2];
scanf("%d %d %d", &n, &A, &B);
for (int i = 1; i <= n; ++i) {
scanf("%s", str + 1);
for (int j = 1; j <= n; ++j)
if (str[j] == '1')
g[i].push_back(j);
}
for (int i = 1; i <= n; ++i) {
scanf("%d %s", &s[i], str);
city[i].resize(s[i]);
for (int j = 0; j < s[i]; ++j)
city[i][j] = str[j] - '0';
}
}
LL qpow(LL a, LL b) {
LL res(1);
while (b) {
if (b & 1) {
res = res * a % MOD;
}
a = a * a % MOD;
b >>= 1;
}
return res;
}
void init() {
fac[0] = 1;
int N = maxn - 3;
for (int i = 1; i <= N; ++i)
fac[i] = 1ll * fac[i - 1] * i % MOD;
ifac[N] = qpow(fac[N], MOD - 2);
for (int i = N - 1; i >= 0; --i)
ifac[i] = 1ll * ifac[i + 1] * (i + 1) % MOD;
}
vector<bool> colbull[maxn];
int Gcdcol[maxn], cntbull[maxn], maxbull[maxn], minbull[maxn];
int low[maxn], dfn[maxn], dfst, col[maxn], colcnt, stk[maxn], top;
void tarjan(int u) {
dfn[u] = low[u] = ++dfst;
stk[++top] = u;
for (int i = 0; i < (int)g[u].size(); ++i) {
int v= g[u][i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (!col[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
++colcnt;
int v;
do {
v = stk[top--];
col[v] = colcnt;
} while (u != v);
Gcdcol[colcnt] = s[u];
}
}
void solve1() {
for (int i = 1; i <= n; ++i)
if (!dfn[i])
tarjan(i);
for (int i = 1; i <= n; ++i)
Gcdcol[col[i]] = __gcd(Gcdcol[col[i]], s[i]);
for (int i = 1; i <= n; ++i) {
colbull[col[i]].resize(Gcdcol[col[i]]);
for (int j = 0; j < s[i]; ++j)
if (city[i][j] == 1) {
colbull[col[i]][j % Gcdcol[col[i]]] = 1;
}
}
vector<bool> tmp;
for (int i = colcnt; i >= 2; --i) {
int g = __gcd(Gcdcol[i], Gcdcol[i - 1]);
tmp.clear();
tmp.resize(g);
for (int j = 0; j < Gcdcol[i]; ++j)
tmp[j % g] = tmp[j % g] | colbull[i][j];
for (int j = 0; j < Gcdcol[i - 1]; ++j)
colbull[i - 1][j] = colbull[i - 1][j] | tmp[j % g];
}
for (int i = 1; i <= colcnt; ++i)
for (int j = 0; j < Gcdcol[i]; ++j)
cntbull[i] += colbull[i][j];
for (int i = 1; i <= n; ++i)
maxbull[i] = s[i] / Gcdcol[col[i]] * cntbull[col[i]];
for (int i = 1; i <= n; ++i)
for (int j = 0; j < s[i]; ++j)
minbull[i] += city[i][j];
}
LL ans;
LL combine(int n, int m) {
if (m < 0 || n < 0 || m > n) return 0;
return 1ll * fac[n] * ifac[m] % MOD * ifac[n - m] % MOD;
}
void solve2() {
for (int i = 1; i <= n; ++i) {
int cnt1 = 0, cnt2 = 0;
for (int j = 1; j <= n; ++j) {
if (i == j) continue;
if (minbull[j] > maxbull[i]) ++cnt1;
else if (maxbull[j] > maxbull[i] || (maxbull[j] == maxbull[i] and j < i)) ++cnt2;
}
if (cnt1 >= A) continue;
for (int j = min(B - 1, min(cnt2, A - 1 - cnt1)); j >= B - cnt1 - 1 && j >= 0; j--) {
ans = (1ll * ans + 1ll * combine(cnt1, B - j - 1) * combine(cnt2, j) % MOD) % MOD;
}
}
cout << ans << endl;
}
int main() {
// freopen("fake.in", "r", stdin);
// freopen("fake.out", "w", stdout);
input();
init();
solve1();
solve2();
return 0;
}