二叉查找树在极端情况下会演变成一棵只有一侧子孩子的树,例如每个非叶子只有左孩子或者右孩子,这时候在查找的时候就需要遍历这棵树来找到目标值,它的快速搜索价值就体现不出来了,如果这棵搜索树在构建的时候,能够平衡左右子树的身高差,使得左右子树身高差不超过1,那它的搜索效率就是O(lgn),平衡二叉树就是这样的树,它有以下特点:
1、左右子树的高度差不超过1
2、左右子树都是平衡二叉树,空节点也视其为一棵平衡二叉树
以上有点递归定义问题的意思,平衡二叉树的关键特性是其任何一个节点为根的左右子树高度差不能超过1,因为有这个特性限制,所以在创建平衡二叉树的时候如果发现这个平衡被打破了,需要对树进行旋转操作,以恢复其平衡的性质,具体的旋转有以下几种情况:
1、LL类型旋转(单向向右):这种情况下是某个节点的左孩子的左子树导致该节点失衡,需要对该节点进行向右旋转,如下图:
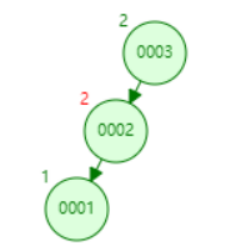
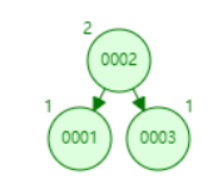
如上图,值为3的节点,当它只有一个左孩子2时,此时左右孩子的高度差是1,当再插入1时,它的左右孩子的高度差变成了2,需要对其进行右旋:
LL_Rotate(node):
leftNode=node.left;//待旋转节点的左孩子
leftRightNode=leftNode;//待旋转节点的左孩子的右孩子
leftNode.right=node;//更新左孩子节点,将自己作为作为左孩子的右节点,即上图中3变成了2的右孩子
node.left=leftRightNode;//更新自己的左孩子,
node.height=max(node.left.height,node.right.height)+1;//更新高度
leftNode.height=max(leftNode.left.height,leftNode.right.height)+1;//跟新新的根节点高度,需要先更新node节点...
return leftNode;//返回左孩子替代自己的位置,比如上图中,2替代了3的位置
2、RR类型旋转(单向向左):这种情况下是某个节点的右孩子的右子树导致该节点失衡,需要对该节点进行向左旋转,如下图:
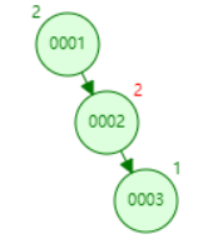
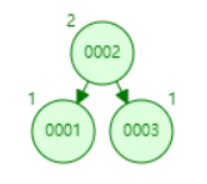
如上图,因为3的插入,根节点1的平衡因子变成2,需要对1进行左旋,方向与LL完全相反:
RR_Rotate(node):
rightNode=node.right;//获取右孩子
rightLeftNode=rightNode.left;//获取右孩子的左孩子
rightNode.left=node;//更新右孩子
node.right=rightLeftNode;
node.height=max(node.left.height,node.right.height)+1;
rightNode.height=max(rightNode.left.height,right.right.height)+1;
return rightNode;//返回
3、LR类型旋转(先左后右):这种情况下是某个节点的左孩子的右子树导致该节点失衡,需要对该节点的左孩子进行左旋,然后再对其进行右旋,如下图:
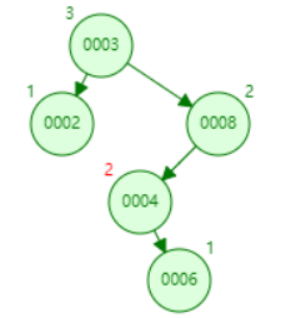

如上图,节点值为8的节点的左孩子,因为6的插入,导致8节点失衡,需要先对左孩子4进行左旋,由6替代4的位置,再对8进行右旋,由6替代8:
Left_Right_Rotate(node):
node.left=LL_Rotate(node.left);//对左孩子左旋
return RR_Rotate(node);//对自己进行右旋
4、RL类型旋转(先右后左):这种情况下是某个节点的右孩子的左子树导致该节点失衡,需要对该节点的右孩子进行右旋,然后再对其进行左旋,如下图:
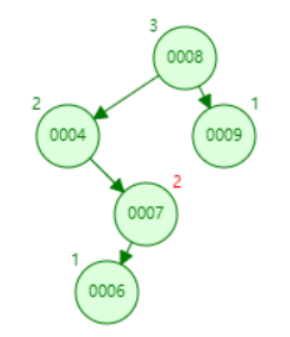
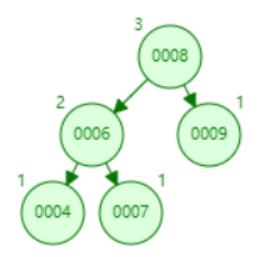
如上图,4的平衡因子因为其右孩子7新增了一个左孩子节点6而打破,需要对节点7先右旋,再对4进行左旋,同LR完全相反,伪代码如下:
Right_Left_Rotate(node):
node.right=RR_Rotate(node.right);//对右孩子进行右旋
return LL_Rotate(node);//对自身进行左旋
节点的高度的获取:
Get_Height(node):
if node==null:
return 0;
leftHeight=Get_Height(node.left);
rightHeight=Get_Height(node.right);
return max(leftHeight,rightHeight)+1;
平衡因子的获取,某个节点的平衡因子是由左右子树的高度差决定的:
Get_Factor(node):
return Get_Height(node.left)-Get_Height(node.right);
节点的平衡调整,涉及到左旋、右旋、左右旋转、右左旋转:
balance(node):
if node==null
return null;
//左子树导致不平衡
if getFactor(node)==2 :
//左孩子的左子树导致不平衡
if getFactor(node.left)==1:
node=LL_Rotate(node)
else:
//左孩子的右子树导致不平衡
node=Left_Right_Rotate(node);
//右子树导致不平衡
else if getFactor(node)==-2:
右子树的右孩子导致不平衡
if getFactor(node.right)==-1:
node=RR_Rotate(node);
else
//右孩子的左子树导致不平衡
node=Right_Left_Rotate(node);
//返回旋转后的节点
return node;
树的插入操作:
insert_val(node,val):
if node==null:
return new Node(val);
//这里是一个递归创建过程
if val<node.val:
node.left=insert_val(node.left,val);
node.left.parent=node;
else
node.right=insert_val(node.right,val);
node.right.parent=node;
//返回调整后的节点
return balance(node);
树的删除操作,删除操作有点复杂,需要找到那个替代自己的节点,其方法就是寻找删除节点的左子树的最大值;如果待删除节点没有左子树,则需要寻找
右子树的最小值,如果待删除的节点是叶子节点,则直接删除即可:
delete_node(node,val):
if node==null:
return;//没有找到,直接返回
if val < node.val:
delete_node(node.left,val);
else if val > node.val:
delete_node(node.right,val);
else: //寻找到了目标节点
//目标节点是叶子节点
if node.left==null && node.right==null:
parent=node.parent;
//待删除的节点是根节点
if parent==null:
root=null;
else if parent.left==node:
parent.left=null;
else: //删除节点
parent.right=null;
else if node.left!=null:
left=node.left
maxNode=left
while left!=null:
maxNode=right;
left=left.right;
node.val=maxNode.val
delete_node(node.left,node.val);
else: //与上面node.left!=null中的left相反,将left修改为right
balance(node);//调节树的平衡
以上AVL树的构建分析完毕,其中关键点为节点的平衡操作,创建和删除节点时使用到了递归操作,算是一个设计技巧,如下为完整的示例代码:

package avl; import java.util.ArrayList; import java.util.List; /** * AVL 树的定义 */ public class AVLTree { //根节点 Node root=null; /** * 插入新值 * @param val * @return */ public AVLTree insertVal(int val){ if(root==null){ root=new Node(val); }else{ insertVal(root,val); } return this; } /** * 节点的插入 * @param node * @param val * @return */ private Node insertVal(Node node,int val){ if(node==null){ node=new Node(val); return node; } if(val<node.val){ Node left=insertVal(node.left,val); node.left=left; left.parent=node; }else{ Node right=insertVal(node.right,val); node.right=right; right.parent=node; } //调整节点 node=balance(node); return node; } /** * 删除节点 * @param val */ public void deleteVal(int val){ deleteVal(root,val); } private void deleteVal(Node node,int val){ //没有找到,直接返回 if(node==null){ return; }else if(val<node.val){ deleteVal(node.left,val); balance(node); }else if(val>node.val){ deleteVal(node.right,val); balance(node); }else{ //叶子节点,直接删除 if(node.left==null && node.right==null){ Node parent=node.parent; if(parent==null){ root=null; } if(parent.left==node){ parent.left=null; }else{ parent.right=null; } }else{ //如果左子树不为空,寻找其最大的后继节点 if(node.left!=null){ Node left=node.left; Node maxNode=left; //注意这里是怎么找最大的后继节点的 while(left!=null){ maxNode=left; left=left.right; } node.val=maxNode.val; deleteVal(node.left,maxNode.val); balance(node); }else{ Node right=node.right; Node maxNode=right; while(right!=null){ maxNode=right; right=right.left; } node.val=maxNode.val; deleteVal(node.right,maxNode.val); balance(node); } } } } /** * 平衡节点的操作动作 * @param node * @return */ private Node balance(Node node){ if(node==null){ return null; } if(getFactor(node)==2){ if(getFactor(node.left)==1){ node= LL_Rotate(node); }else{ node= LR_Rotate(node); } }else if(getFactor(node)==-2){ if(getFactor(node.right)==-1){ node= RR_Rotate(node); }else{ node= RL_Rotate(node); } } return node; } /** * 获取节点的高度 * @param node * @return */ private int getHeight(Node node){ if(node==null){ return 0; } int left=getHeight(node.left); int right=getHeight(node.right); int max=Math.max(left,right); return max+1; } /** * 获取节点的平衡因子 * @param node * @return */ private int getFactor(Node node){ if(node==null){ return 0; } return getHeight(node.left)-getHeight(node.right); } /** * 先右后左 * @param node * @return */ private Node RL_Rotate(Node node){ Node right=LL_Rotate(node.right); node.right=right; right.parent=node; return RR_Rotate(node); } /** * 先左后右 * @param node * @return */ private Node LR_Rotate(Node node){ Node left=RR_Rotate(node.left); node.left=left; left.parent=node; return LL_Rotate(node); } /** * 单向左旋 * @param node * @return */ private Node RR_Rotate(Node node){ Node right=node.right,parent=node.parent; Node rightLeft=right.left; right.left=node; node.parent=right; node.right=rightLeft; if(rightLeft!=null){ rightLeft.parent=node; } right.parent=parent; if(parent!=null){ if(parent.left==node){ parent.left=right; }else{ parent.right=right; } }else{ root=right; } return right; } /** * 单向右旋 * @param node * @return */ private Node LL_Rotate(Node node){ Node left=node.left,parent=node.parent; Node leftRight=left.right; left.right=node; node.parent=left; node.left=leftRight; if(leftRight!=null){ leftRight.parent=node; } left.parent=parent; if(parent!=null){ if(parent.left==node){ parent.left=left; }else{ parent.right=left; } }else{ root=left; } return left; } /** * 先序遍历 * @param node */ public void preOrder(Node node){ if(node!=null){ System.out.print(node); preOrder(node.left); preOrder(node.right); } } /** * 中序遍历 * @param node */ public void inOrder(Node node){ if(node!=null){ inOrder(node.left); System.out.print(node); inOrder(node.right); } } /** * 后序遍历 * @param node */ public void postOrder(Node node){ if(node!=null){ postOrder(node.left); postOrder(node.right); System.out.print(node); } } /** * 按层遍历树 */ public void printByLevel(){ System.out.println("========================="); List<Node> temp=new ArrayList<>(); if(root!=null){ temp.add(root); } while(temp.size()>0){ List<Node> nodes=new ArrayList<>(); temp.stream().forEach(obj-> { System.out.print(obj); if(obj.left!=null){ nodes.add(obj.left); } if(obj.right!=null){ nodes.add(obj.right); } }); System.out.println(); temp.clear(); temp.addAll(nodes); } } public static void main(String[] args) { AVLTree tree=new AVLTree(); tree.insertVal(1).insertVal(2).insertVal(3).insertVal(4).insertVal(5).insertVal(7).insertVal(6); tree.printByLevel(); tree.deleteVal(6); tree.printByLevel(); tree.deleteVal(4); tree.printByLevel(); } } class Node{ public int val; public Node left,right,parent; public Node(int val){ this.val=val; } @Override public String toString() { return val+" "; } }
