线性递归和尾递归

线性递归，就是大家平常说的递归，线性递归函数的最后一步操作不是递归操作，将最终条件代入计算。在每次递归调用时，递归函数中的参数，局部变量等都要保存在栈中，当数据量很大的时候，会造成栈溢出。

尾递归，也就是线性迭代，尾递归函数的最后一步操作是递归，也即在进行递归之前，把全部的操作先执行完，这样的好处是，不用花费大量的栈空间来保存上次递归中的参数、局部变量等，这是因为上次递归操作结束后，已经将之前的数据计算出来，传递给当前的递归函数，这样上次递归中的局部变量和参数等就会被删除，释放空间，从而不会造成栈溢出。但是很多编译器并没有自动对尾递归优化的功能，也即当编译器判断出当前所执行的操作是递归操作时，不会理会它究竟是线性递归还是尾递归，这样也就不会删除掉之前的局部变量和参数等。另外，尾部递归一般都可转化为循环语句。

我们用阶乘的例子来看这两者的区别：
   阶乘: 5!=1*2*3*4*5    结果为:120
线性递归:
long Rescuvie(long n)
 {      
  return(n == 1) ? 1 : n * Rescuvie(n - 1);      
}      
调用过程如：
当n = 5时
对于线性递归, 他的递归过程如下:
Rescuvie(5)  
开始调用
{5 * Rescuvie(4)}
{5 * {4 * Rescuvie(3)}}
{5 * {4 * {3 * Rescuvie(2)}}}
{5 * {4 * {3 * {2 * Rescuvie(1)}}}}
{5 * {4 * {3 * {2 * 1}}}}
{5 * {4 * {3 * 2}}}
{5 * {4 * 6}}
{5 * 24}
120

尾递归:
long TailRescuvie(long n, long a) {      
  return(n == 1) ? a : TailRescuvie(n - 1, a * n);        
}      

对于尾递归, 他的递归过程如下:
TailRescuvie(5)
TailRescuvie(5, 1)
TailRescuvie(4, 5)
TailRescuvie(3, 20)
TailRescuvie(2, 60)
TailRescuvie(1, 120)
120

 

尾递归易于在编译器层面优化。如果编译器未作优化，效果和线性递归差不多。

 

分别用线性递归和尾递归来解决经典的猴子吃桃问题

猴子第一天摘下若干个桃子，当即吃了一半，还不过瘾就多吃了一个。第二天早上又将剩下的桃子吃了一半，还是不过瘾又多

吃了一个。以后每天都吃前一天剩下的一半再加一个。到第10天刚好剩一个。问猴子第一天摘了多少个桃子？

线性递归方式

 

#include <iostream>
using namespace std;
int AllSum(int day)
{
	if(day==10)
		return 1;
	else
		return 2*AllSum(day+1)+2;
}
int main()
{
	int sum=AllSum(1);
	cout<<"第一天共摘了"<<sum<<"个桃子"<<endl;
	return 0;
}

　　

运行结果截图：

 

 

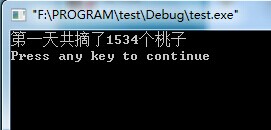
尾递归的实现方式

 

#include<iostream>
using namespace std;
int AllSum(int day,int total)
{
	if(day==10)
		return total;
	else
		return AllSum(day+1,total*2+2);
}
int main()
{
	int sum=AllSum(1,1);
	cout<<"第一天共摘了"<<sum<<"个桃子"<<endl;
	return 0;
}

　　

运行结果截图：

 

 

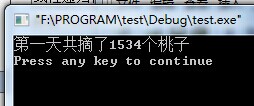
 关于线性递归和尾递归深度的研究学习可以参考  http://blog.zhaojie.me/2009/04/tail-recursion-explanation.html