（注：本文内容和图片来源于林轩田老师的《机器学习基石》课程）
1 引入逻辑回归
通常的二分类问题，希望输出类别；soft的二分类问题，希望输出概率值：
对于soft问题的理想数据和实际数据：
逻辑回归的思想：先求出特征的线性加权分数，再把它用逻辑斯蒂函数转化为0～1之间的值：
逻辑斯蒂函数介绍：
2 逻辑回归的损失函数
最大似然：将训练集产生的概率最大化：
运用逻辑斯蒂函数的性质：
可以得到：
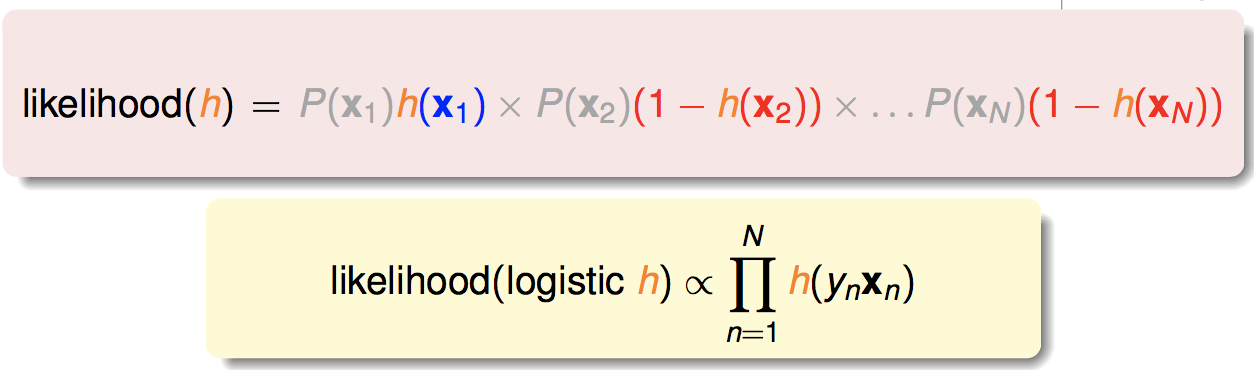
因此问题就变为，选择合适的逻辑回归模型h，使得似然函数最大化：
把逻辑回归模型代进去，具体来说，就是：
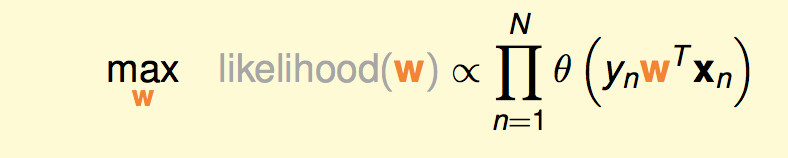
两边取对数：
最后得到最终形式：
3 最小化损失函数
现在的问题是：
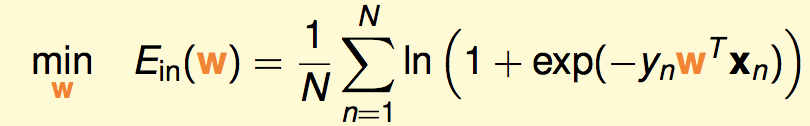
3.1 求损失函数的梯度
3.2 梯度下降法的推导
用迭代来求最优化问题，如下（其中v是一个单位向量）：
梯度下降的思想是：每次更新完以后，函数值尽可能下降到最低。因此相当于：
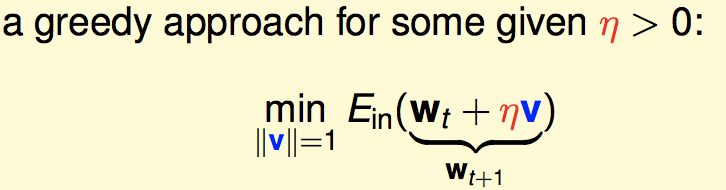
将式子泰勒展开：
则最小化问题变为：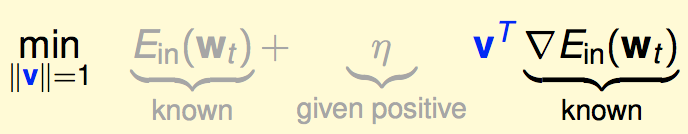
前面一项是已知的，为了将最后一项向量内积最小化，v应该等于：
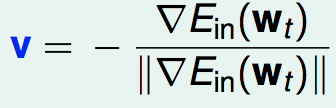（即与梯度相反，再单位化）
η的选择：
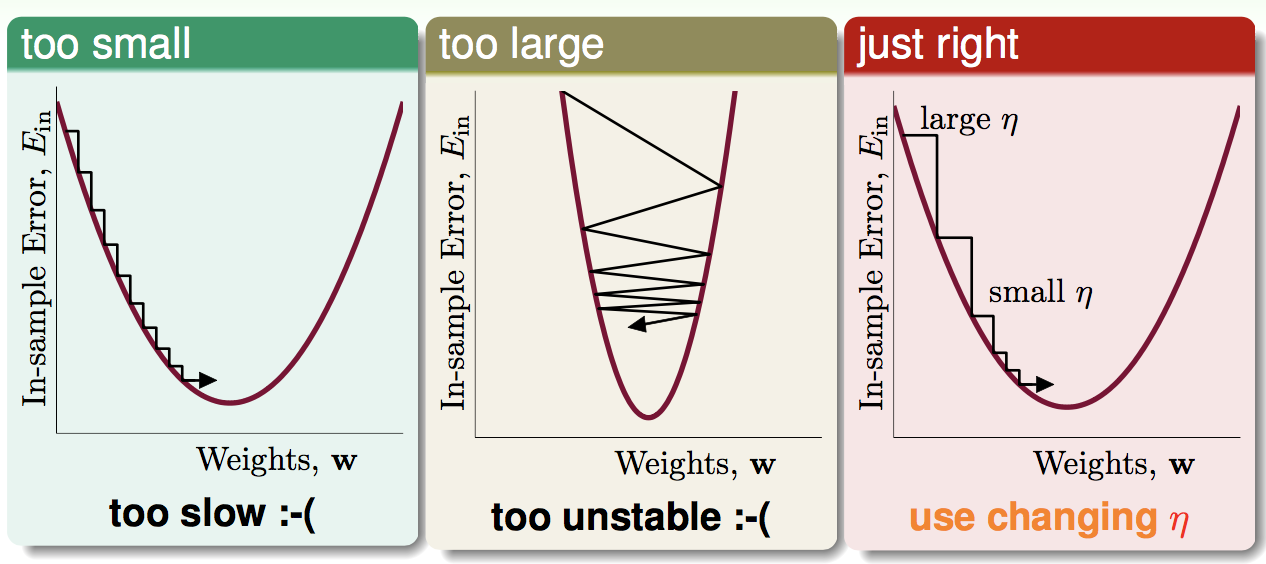
因此η应该随梯度动态变化，假设η正比于梯度的大小：
因此，我们就能得到最后的形式。
4 逻辑回归学习算法
