目标：
1）创建图的表征矩阵
2）分解：计算矩阵的特征值和特征向量；基于一个或多个特征值，将每个点表示成低维的表征
3）分组：基于新的表征，进行聚类
例如，二分图中如何确定好的分类？类间差异大，类内差异小
最小割集
考虑：
1）团外的连接性
2）团内的连接性
团间的连接性与每个团的密度相关
spectral graph partitioning 谱图分割
无向图G的邻接矩阵A
x是n维的特征向量，可认为是G中每个节点的label或者value
那么Ax等到的结果的意义是？
yi是节点i的邻居节点的label的和
通过yi生成新的x value
谱图理论：
分析G的表征矩阵的spectrum
spectrum的意义：图的特征向量xi，（由特征值大小排序而得）
一个例子：假设G中的所有节点的度都有d，G是连通的。那么，G的特征值和特征向量是？
d是A的最大特征值
若G不是完全连通的
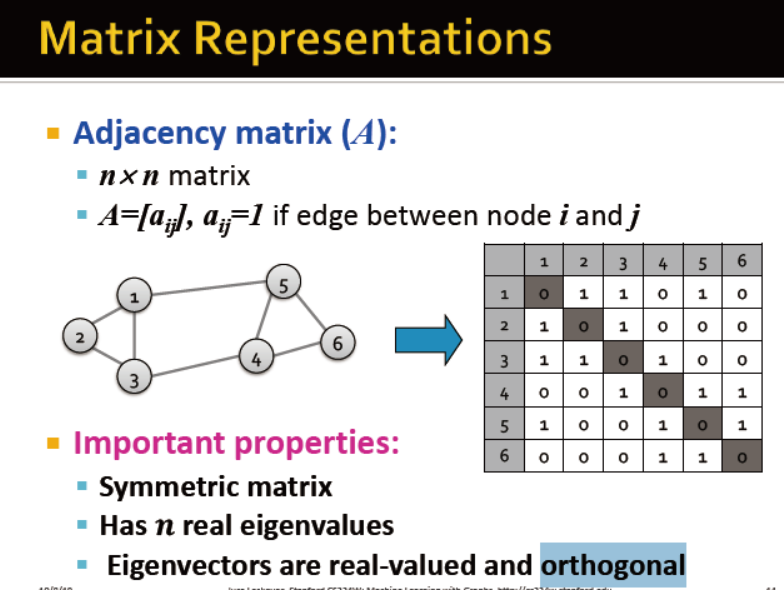
矩阵表征
邻接矩阵：对称矩阵，有n个特征值，特征向量是实数且是正交的
度矩阵：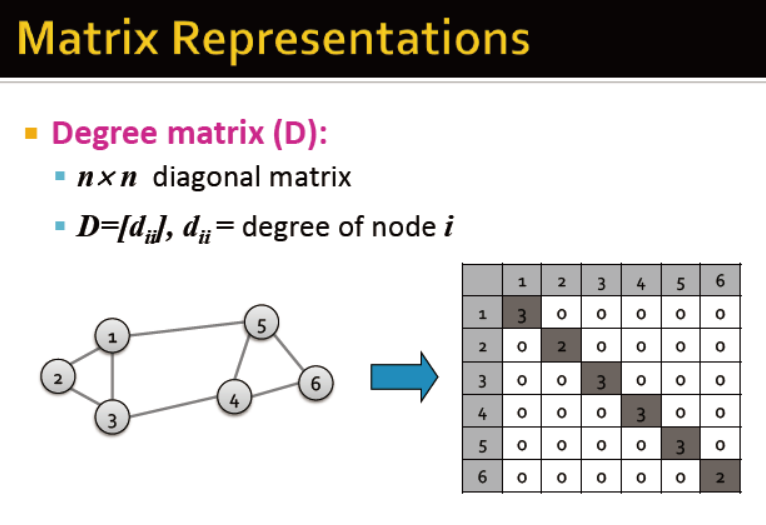
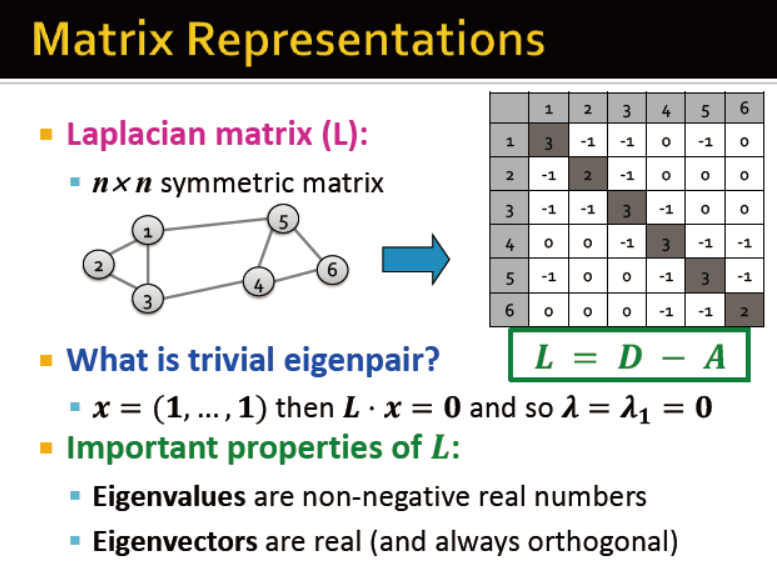
拉普拉斯矩阵：L=D-A
对称矩阵
λ=λ1=0 ？？
特征值为非负实数
特征向量是实数且永远正交
对于对称矩阵M，λ2的值由一公式可定 为xi--xj的平方和
找到最优的x
发现最优的割法
谱聚类算法：
1）图的表征矩阵
2）矩阵的特征值和特征向量；基于特征向量生成每个店的低维向量
3）分组
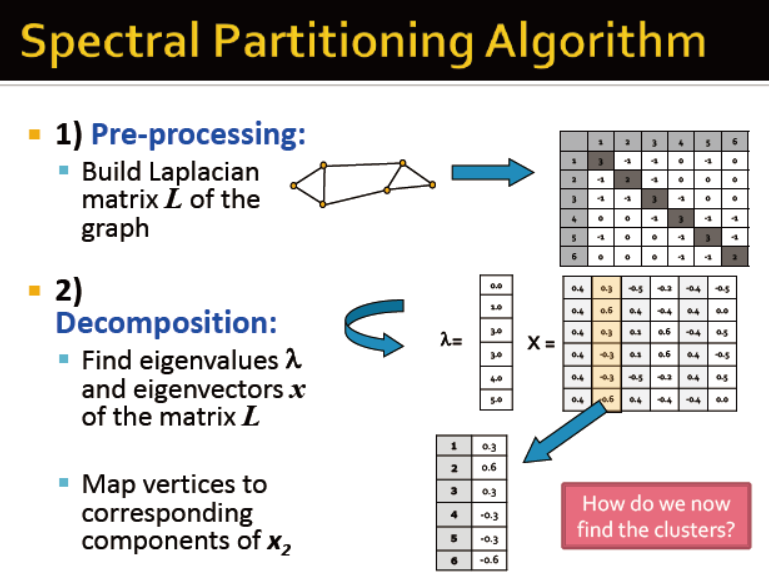
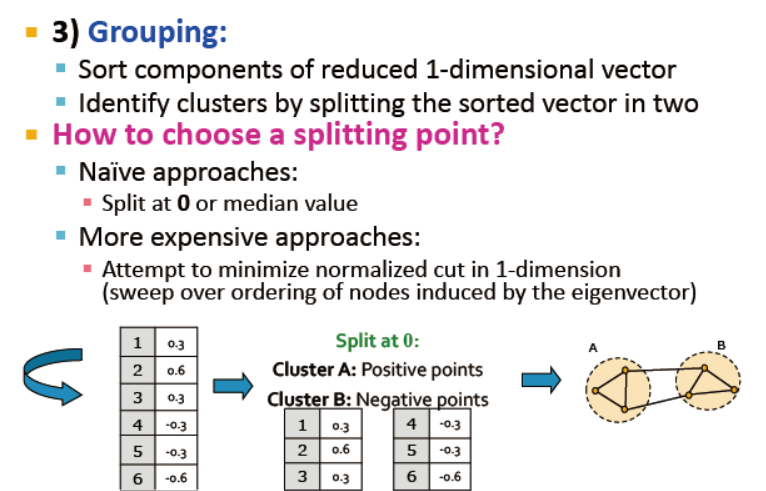
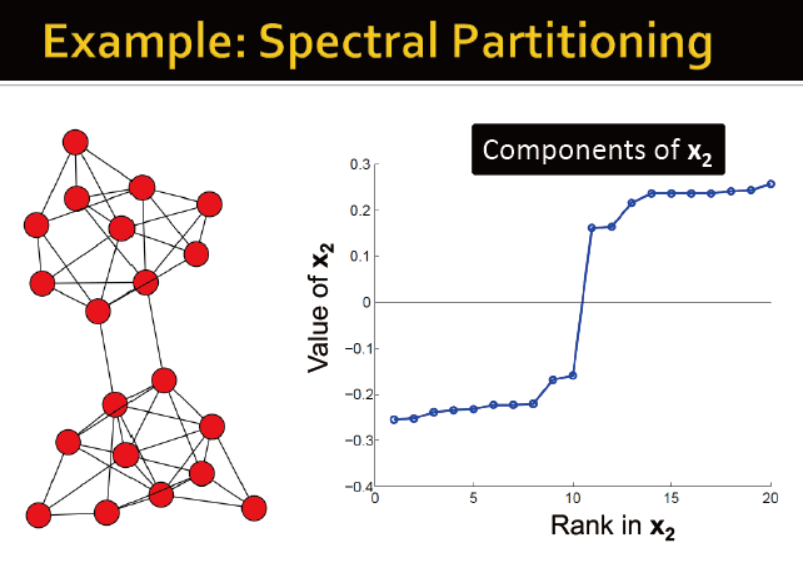
例子
k-way spectral clustering k聚类
1）迭代的二分类
2）对eigenvector多聚类
如何选择最优k——从特征值中，挑选间隔最大的两个相邻值
基于motif的谱聚类
基于连接模式进行聚类~
主题1：发现motif的模块
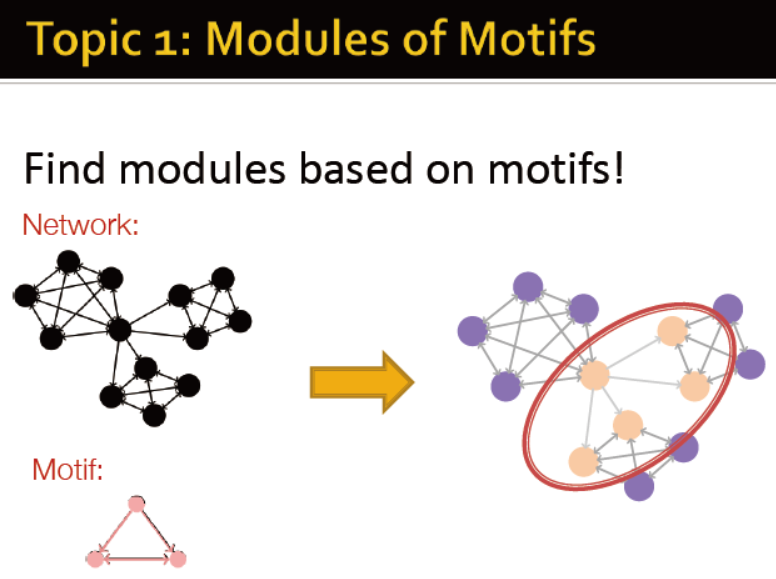
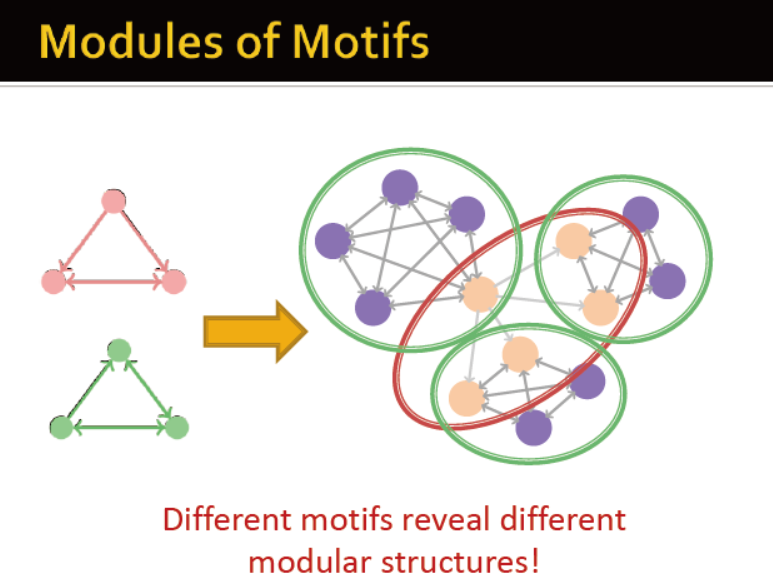
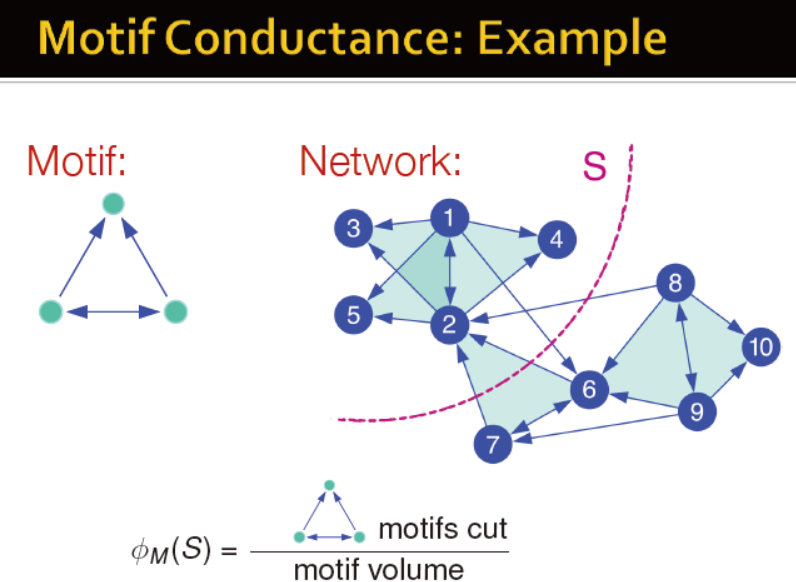
定义motif conductance
生成motif是的cut和volumn
找到节点集S使motif conductance最小， 但找到s较难
解决方案：通过谱的方法
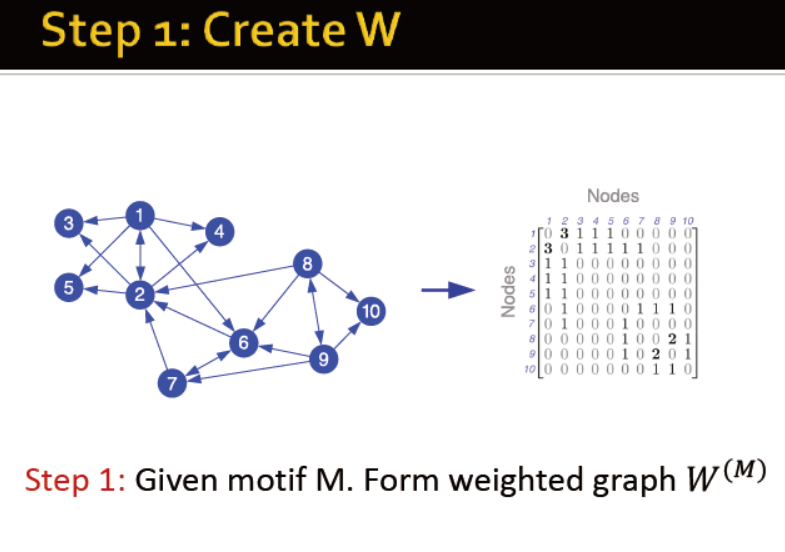
步骤：
1）生成权重矩阵，值为该边参与生成motif的次数
2）谱聚类的方法
3）分组
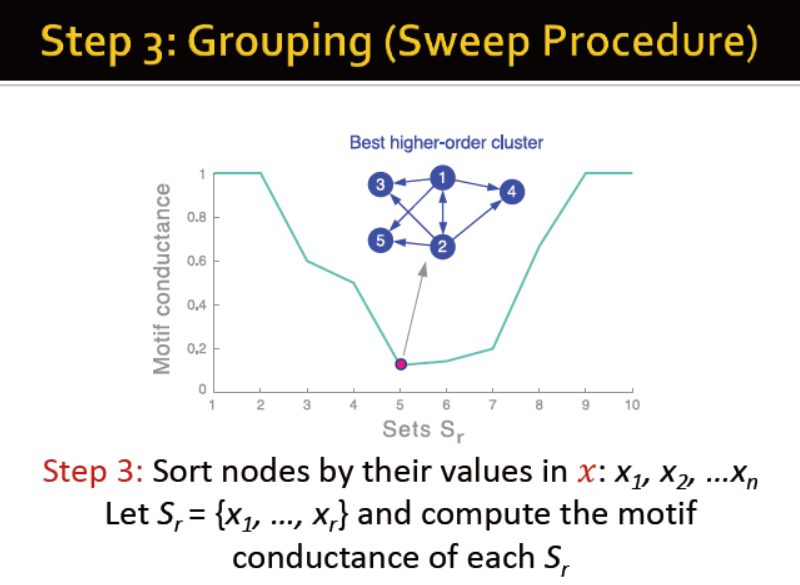
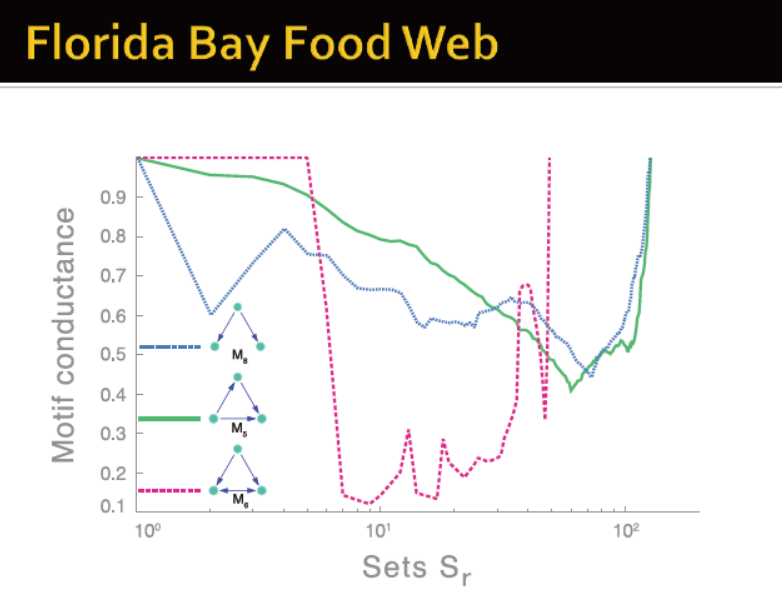
两个例子：食物链中未知的motif； 通信网络中已知的motif
未知的——每个motif跑一遍，找最小的
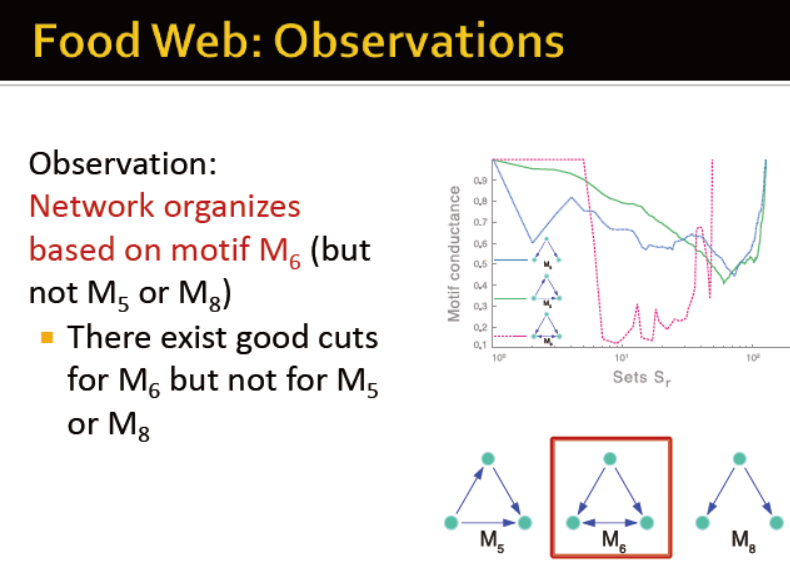
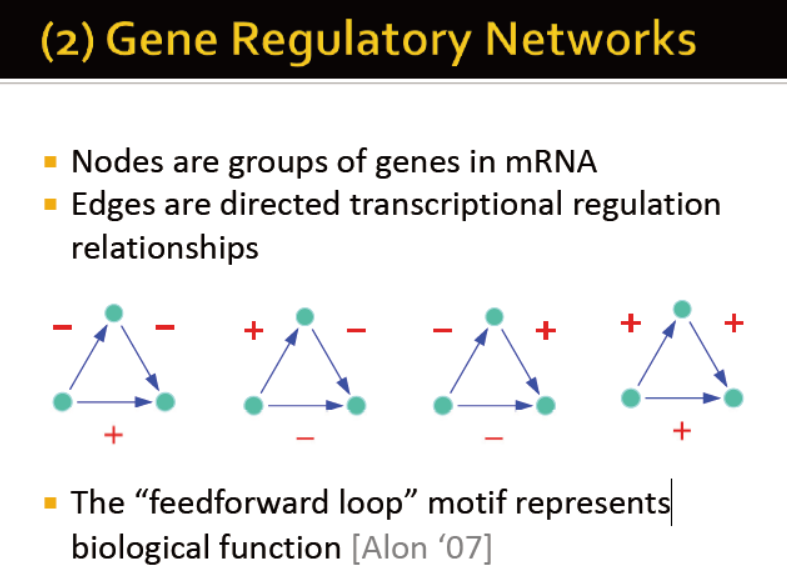
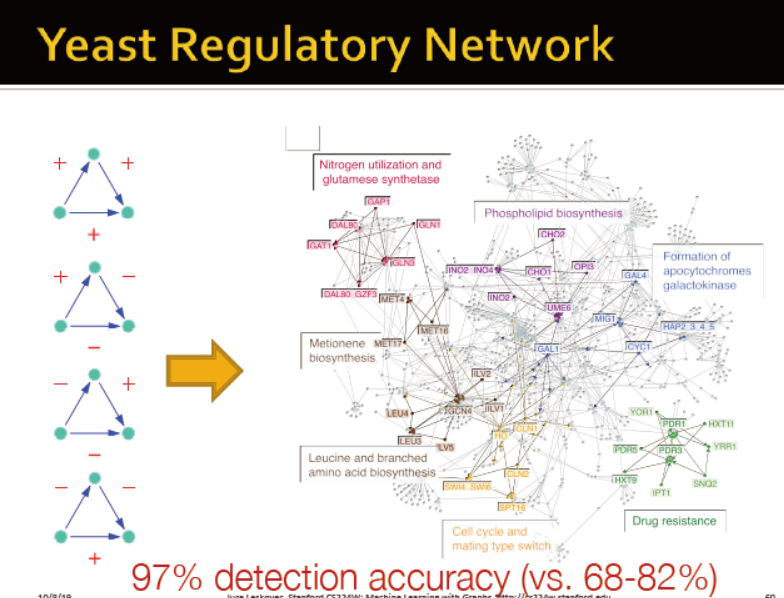
基因管理网络
