【ybtoj】【倍增问题】货车运输

题意

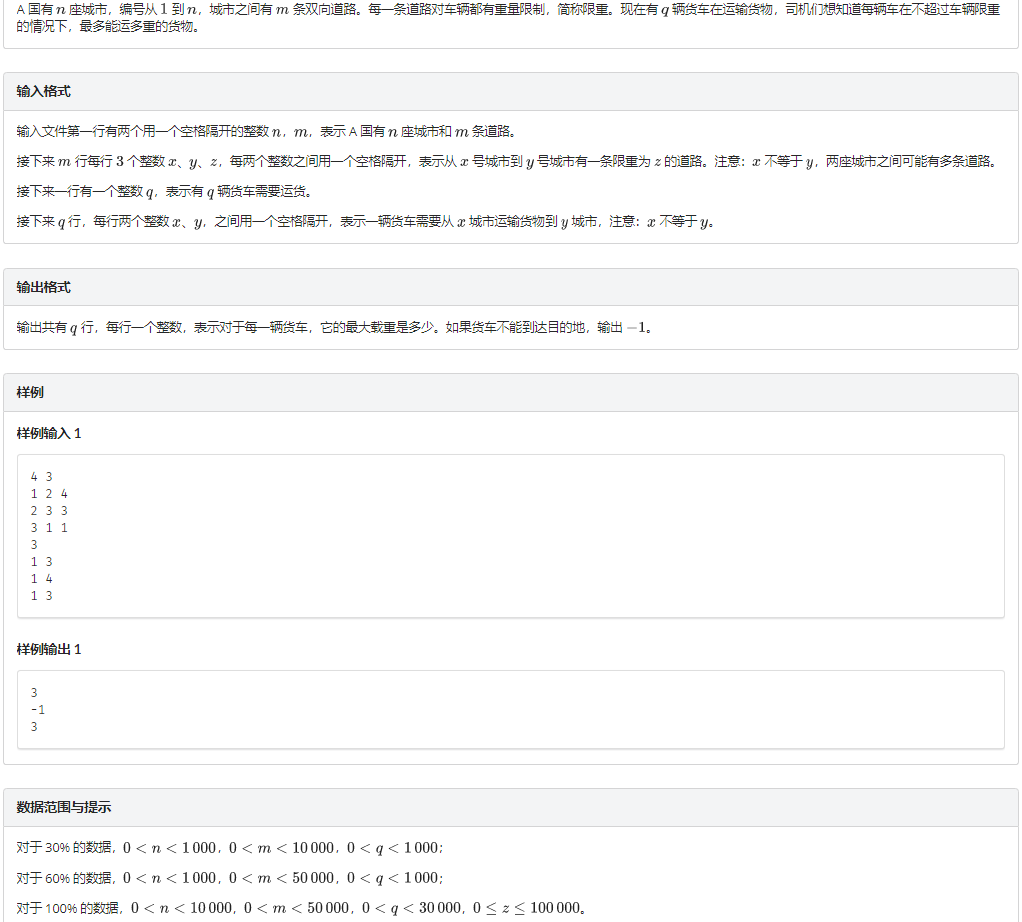
题解

好题啊...可惜我做的时候就像嗑药了，打了乱七八糟一堆bug...

首先要看出最优路径一定是一个最大生成森林。

最大没得说，因为要尽量让权值大。

证明是森林：对于已经生成的一棵树（或者说森林），如果再加入一条非树边 $c->d$,那么原本树上 $c->d$ 的答案一定比新加入这条边的答案好，所以是森林

知道是森林就可以用LCA了，在求$f[u][i]$的过程中顺便求一个$dis[u][i]$记录路径上的最小值（我就是这个简单的$dp$手残写错了） 所以总结一下：先用个$kruskal$求出最小生成树，再跑一遍树上$LCA$即可

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e4+10,M = 5e4+10;
int n,m,q,tot;
int f[N][21],vis[N],dep[N],dis[N][21],fa[N];
int ecnt=-1,head[M<<1];
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
struct edge
{
	int nxt,to,w;
}a[M<<1];
void add(int x,int y,int w)
{
	a[++ecnt]=(edge){head[x],y,w};
	head[x]=ecnt;
}
void dfs(int u,int fa,int num)
{
	vis[u]=num;
	//printf("u=%d
",u);
	for(int i=1;i<=18;i++) 
		f[u][i]=f[f[u][i-1]][i-1],
		dis[u][i]=min(dis[u][i-1],dis[f[u][i-1]][i-1]);
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue;
		f[v][0]=u;
		dis[v][0]=a[i].w;
		dep[v]=dep[u]+1;
		dfs(v,u,num);
	}
}
struct K
{
	int x,y,w;
}k[M<<1];
bool cmp(K a,K b){return a.w>b.w;}
void init(){for(int i=1;i<=n;i++) fa[i]=i;}
int find(int x)
{
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}
int lca(int x,int y)
{
	int ans=INF;
	//printf("vis[x]=%d,vis[y]=%d
",vis[x],vis[y]);
	if(vis[x]!=vis[y])return -1;
	if(dep[x]<dep[y]) swap(x,y);
	//printf("x=%d,y=%d
",x,y);
	//printf("f[3][0]=%d ",f[3][0]);
	for(int i=18;i>=0;i--)
	{
		if(f[x][i]&&dep[f[x][i]]>=dep[y]) 
		{
			//printf("ans=%d
",ans);
			ans=min(ans,dis[x][i]),x=f[x][i];
		}
	}
	if(x==y)return ans;
	for(int i=18;i>=0;i--)
		if(f[x][i]!=f[y][i]) 
		{
			//printf("ans=%d
",ans);
			ans=min(ans,min(dis[x][i],dis[y][i])),
			x=f[x][i],y=f[y][i];
		}
	ans=min(ans,min(dis[x][0],dis[y][0]));
	return ans;
}

int main()
{
	memset(head,-1,sizeof(head));
	
	n=read(),m=read();
	init();
	for(int i=1;i<=m;i++) 
		k[i].x=read(),k[i].y=read(),k[i].w=read(); 
	sort(k+1,k+m+1,cmp);
	for(int i=1;i<=m;i++)
	{
		int x=k[i].x,y=k[i].y;
		if(find(x)!=find(y))
		{
			//printf("ok ");
			fa[fa[x]]=fa[y];
			add(x,y,k[i].w),add(y,x,k[i].w);
		}
	}
	for(int i=1;i<=n;i++)
		if(!vis[i]) tot++,dfs(i,-1,tot);
	q=read();
	while(q--)
	{
		int x=read(),y=read();
		printf("%d
",lca(x,y));
	}
	return 0;
}