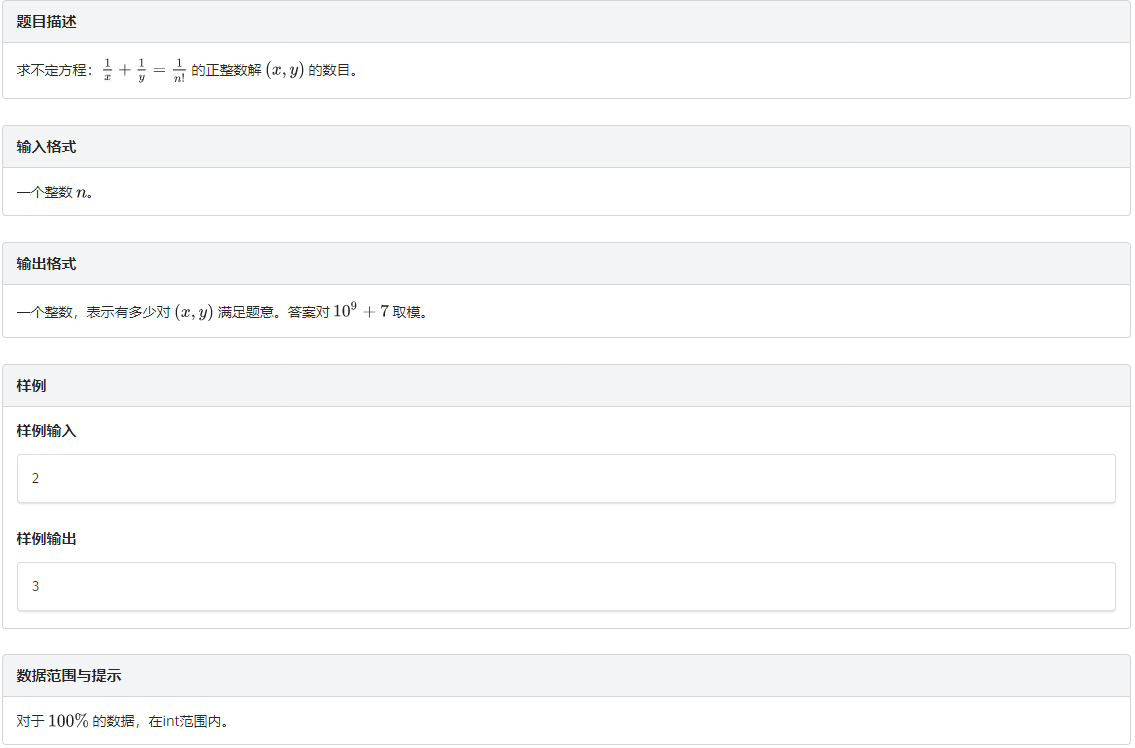
题意
题解
首先面对这种不定方程,先转化成 (x=k imes y) 的形式,本题中即 (y=dfrac{xn!}{x-n!}).
设 (t=x-n!) ,则 (y=n!+dfrac{(n!)^2}{t}).
那么问题转化成求 ((n!)^2) 的约数个数。
这里由于 (n!) 非常大,所以不能用常规的试除法 (O(sqrt{n})) 求出其所有约数。
引入一种方法快速求出 (n!) 的约数个数。
先求出 (n) 中所有的质数,接着...先看代码:
pre();
for(int i=1;i<=cnt;i++)
for(ll j=p[i];j<=n;j*=p[i])
{
c[i]+=n/j;
c[i]%=mod;
}
具体是怎么实现的呢?以 (2) 的幂次方的覆盖为例,先看下图:
其中红色表示 (2) 的倍数,绿色表示 (4) 的倍数,蓝色表示 (8) 的倍数。
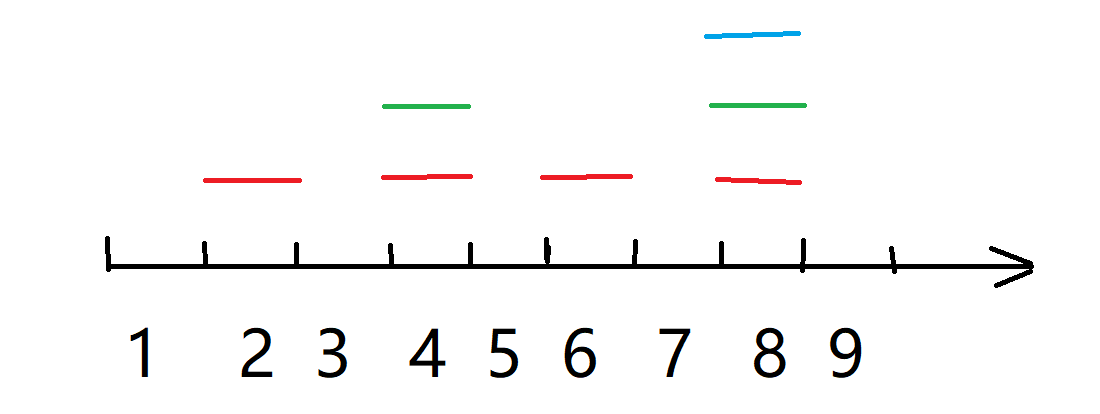
这样的覆盖方法可以发现,(n!) 内的每一个数的质因数个数都会被计入,同时第二维循环只需要枚举到 (n) 即可。
对于 ((n!)^2),累乘 ((2 imes c_i-1)) 即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e7+10,mod = 1e9+7;
inline ll read()
{
ll ret=0;char ch=' ',c=getchar();
while(!(c>='0'&&c<='9')) ch=c,c=getchar();
while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
return ch=='-'?-ret:ret;
}
bool vis[N];
int p[N],cnt,c[N],n;
void pre()
{
vis[2]=0;
for(int i=2;i<=n;i++)
{
if(!vis[i]) p[++cnt]=i;
for(int j=1;j<=cnt&&i*p[j]<=n;j++)
{
vis[i*p[j]]=1;
if(i%p[j]==0) break;
}
}
}
int main()
{
n=read();
pre();
for(int i=1;i<=cnt;i++)
for(ll j=p[i];j<=n;j*=p[i])
{
c[i]+=n/j;
c[i]%=mod;
}
ll ans=1;
for(int i=1;i<=cnt;i++)
ans=(ans*(c[i]*2+1))%mod;
printf("%lld",ans);
return 0;
}