加权有向图

1. 最短路径问题

一个最直观最常用的最短路径问题就是用地图软件或者导航系统来获取从一个地方到另一个地方的路径。在一副加权有向图中，从顶点s到顶点t的最短路径是所有从s到t的路径中的权重最小者。

我们的重点是单点最短路径问题，也就是说给定任意一个顶点，找到其对其他所有顶点的最短路径。

2. 加权有向图的数据结构

加权有向边的数据结构

//加权有向边的数据类型
public class DirectedEdge
{
    private final int v; //边的起点
    private final int w; //边的终点
    private final double weight; //边的权重

    public DirectedEdge(int v, int w, double weight)
    {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }
    
    public double weight()
    { return weight; }

    public int from()
    { return v;}

    public int to()
    { return w;}
    
    public String toString()
    {
        return String.format("%d - %d %.2f", v, w, weight);
    }
}

加权有向图的数据类型

//加权有向图的数据类型
public class EdgeWeightedDigraph
{ 
    private final int V; //顶点数
    private int E;       //边数
    private Bag<DirectedEdge>[] adj; //邻接表

    public EdgeWeightedDigraph(int V)
    {
        this.V = V;
        this.E = 0;
        adj =(Bag<DirectedEdge>[]) new Bag[V];
        for(int v= 0 ;v<V;v++)
            adj[v] = new Bag<DirectedEdge>();
    }
    
    public void addEdge(DirectedEdge e)
    {
        int v = e.from();
        adj[v].add(e);
        E++;
    }
    public Iterable<DirectedEdge> adj(int v)  { return adj[v];}
    
    public int V()  { return V;}
    public int E()  { return E;}
    
    public Bag<DirectedEdge> edges()
    {
        Bag<DirectedEdge> d = new Bag<DirectedEdge>();
        for(int v=0;v<V;v++)
        {
            for(DirectedEdge e: adj[v])
                d.add(e);
        }
        return d;
    }
}

最短路径的数据结构

从一个顶点s到其他所有顶点的最短路径的集合其实本质是一颗树。因为如果最短路径中存在环的话，那么从s到环中任意一个顶点的距离就不是唯一的，也就不存在最短的定义了。

因此我们本质是要得到一颗最短路径树。

1）最短路径的边。使用一个父链接数组edgeTo[]。edgeTo[v]的值为树中连接v和它的父节点的边（也是从s到v的最短路径上的最后一条边）

2）到达起点的距离。用一个distTo[]数组来存从距离。distTo[v]表示从s到v的最短路径的长度。

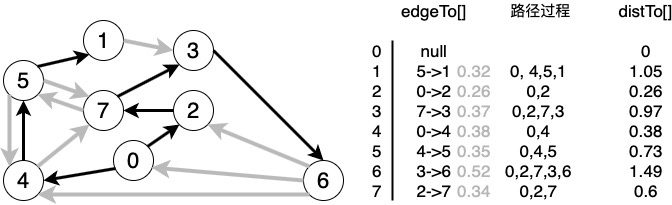
 上图表示的是从0出发的最短路径树。

3. Dijkstra算法（非负权重）

Dijkstra算法本身和即时的prim算法非常接近。prim算法添加的离树最近的边，Dijkstra算法添加的是离起点最近的非树顶点。

只要理解了prim的实现，Dijkstra的算法就非常好理解了。核心还是维护一个distTo[]数组，每访问一个顶点就更新一下数组里的值，直到所有的顶点访问后，数组里存的就是最短路径。

需要注意的是Dijkstra只适用于所有权重为非负的情况。

public class DijkstraSP
{
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    private IndexMinPQ<Double> pq;


    public DijkstraSP(EdgeWeightedDigraph G, int s)
    {
        edgeTo = new DirectedEdge[G.V()];
        distTo = new double[G.V()];
        pq = new IndexMinPQ<>(G.V());
        for(int v=0;v<G.V();v++)
            distTo[v] = Double.POSITIVE_INFINITY;

        distTo[s]  = 0.0;
        pq.insert(s, 0.0);
        while(!pq.isEmpty())
            relax(G, pq.delMin());
    }

    public void relax(EdgeWeightedDigraph G, int v)
    {
        for(DirectedEdge e:G.adj(v))
        {
            int w = e.to();
            if(distTo[w] > distTo[v] + e.weight())
            {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
                if(pq.contains(w)) pq.change(w, distTo[w]);
                else pq.insert(w, distTo[w]);
            }
        }
    }
}

4. 理解负权重

负权重的出现其实不只体现在数学上，在实际应用中其实非常实用。以任务调度为例。

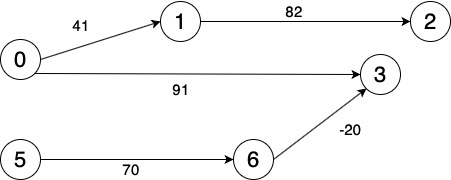
以上图为例。边的权重指的是任务需要的时间。例如任务0需要41个时间单位才能完成，任务0完成后才能开始任务1，任务1需要82个时间单位，然后才能开始任务2...

而6指向3的路径权重为-20，这是指6号任务需要在3号任务开始后的20个时间单位内开始，或者说3号任务不能早于6号任务的20个时间单位。

  

5. 一般的无环加权有向图的最短路径算法（可以处理负权重）

无环加权有向图的算法的核心在于依照有向图的拓扑排序来松弛每条边。而拓扑排序又保证了每条边只会被放松一次，因此这是一种最优的最短路径搜索方法。

public class AcyclicSP
{
    private double[] distTo;
    private DirectedEdge[] edgeTo;

    public AcyclicSP(EdgeWeightedDigraph G, int s)
    {
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];
        for(int v =0 ;v<G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;

        distTo[s] = 0.0;
        Topological top = new Topological(G); //暂未实现的类，只是为了调用来计算有向图的拓扑排序
        for(int v:top.order())
            relax(G, v);
    }

    public void relax(EdgeWeightedDigraph G, int v)
    {
        for(DirectedEdge e: G.adj(v))
        {
            int w = e.to();
            if(distTo[w] > distTo[v] + e.weight())
            {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
            }
        }
    }
}

 6. Bellman - Ford算法

Bellman - Ford算法的特点在于加入了一个用来保存即将被放松的顶点的队列。然后按照队列的顺序放松顶点。

public class BellmanFordSP
{
    private double[] distTo; //距离
    private DirectedEdge[] edgeTo; //最短路径的最后一条边
    private Queue<Integer> queue; //待松弛的顶点
    private boolean[] onQ;  //记录待松弛点，和queue一起使用

    public BellmanFordSP(EdgeWeightedDigraph G, int s)
    {
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];
        onQ = new boolean[G.V()];

        for(int v=0;v<G.V();v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;
        queue.enqueue(s);
        onQ[s] = true;
        while(!queue.isEmpty())
        {
            int v= queue.dequeue();
            onQ[v] = false;
            relax(G, v);
        }
    }

    public void relax(EdgeWeightedDigraph G, int v)
    {
        for(DirectedEdge e:G.adj(v))
        {
            int w = e.to();
            if(distTo[w] > distTo[v] + e.weight()) {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
                if (!onQ[w]) {
                    queue.enqueue(w);
                    onQ[w] = true;
                }
            }
        }
    }
    
   
}

7. 总结

以上所有求有向图最短路径的方法，本质其实都是按一定顺序对所有的顶点做松弛。

Dijkstra算法用了一个优先队列才存储即将要被松弛的点。这样保证每次都是选择当前最短路径的点来做松弛。但是这样做的前提是所有边的权重是正的，否则，选最短的做松弛后结果未必是最短的。

而一般的最短路径方法则巧妙的选择了用有向图的拓扑排序的顺序依次对顶点做松弛，这其实是最为简单，速度最快的方法，而且可以处理负权重。

最后的Bellman - Ford算法用了一个队列来保留上一轮被更新过的顶点。并且相比前两种算法，其实每个顶点的距离可能都被更新过多次。因此最坏情况的效率会低一些，但是更具有通用性。

至此，整个图结构的部分就全部结束了。其实无向图也好，有向图也好，最小生成树，最短路径也好，构建的方法都非常类似，只是具体细节的处理差异。这几篇博客中的代码并非原创，都是摘自《算法》一书中，但是确实是我自己一行一行敲出来的，这个过程也有助于我自己理解和记忆。写到后面就发现，这些代码其实都非常类似。虽然图结构相比之前的一些算法理论上难一些，但代码总体来讲都非常简练。与大家共勉！

参考资料： 《算法》第四版