题目
点这里看题目。
分析
直接变换式子:
[egin{aligned}
h_jle h_i+p_i-sqrt{|i-j|} & Rightarrow p_ile h_j+sqrt{|i-j|}-h_i\
& Rightarrow p_i=lceilmax{h_j+sqrt{|i-j|}-h_i}
ceil\
& Rightarrow p_i=lceilmax{h_j+sqrt{|i-j|}}
ceil-h_i
end{aligned}
]
显然,(|i-j|)可以拆分成(i<j)和(i>j)两个部分,两个部分是相似的,因此我们可以只考虑(i<j)的情况。
考虑到(sqrt{n})的增长速度随(n)的增大而减小,因此会存在“后来的决策点超越前面的决策点”的情况,但绝不存在“前面的决策点超越后来的决策点”的情况。
设(f_i(n)=sqrt{n-i}+h_i),那么我们就正在求解(max_{jle i}{f_j(i)})。
下图展示了样例中(f)函数的情况:
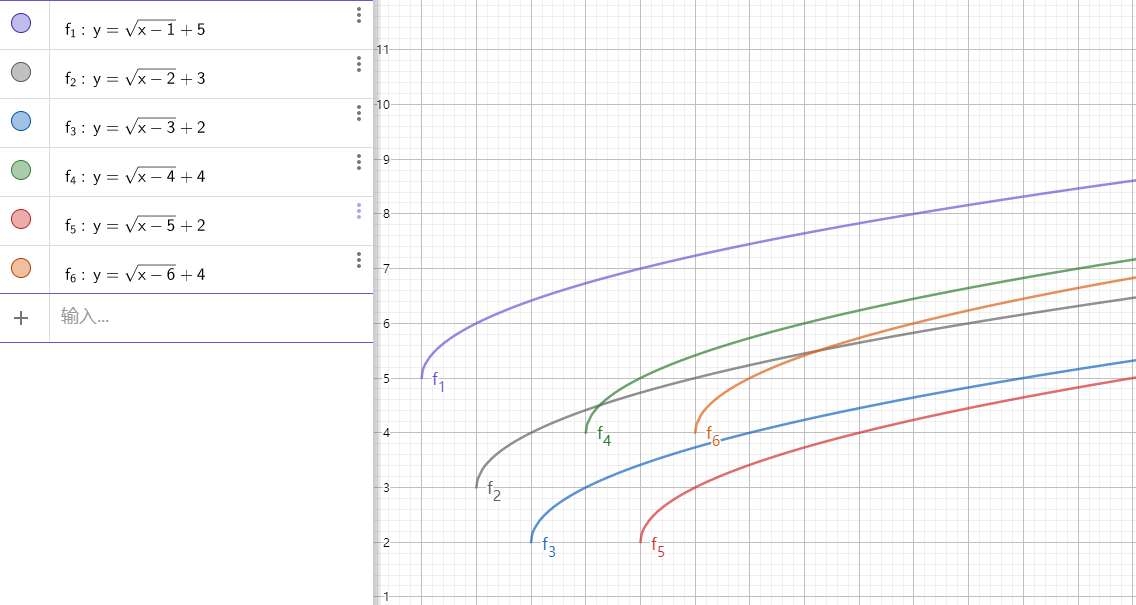
可以发现,两个(f)函数最多有一个交点。那么,对于两个函数,我们就可以二分出它们交点的(x)坐标(没有交点的,我们视为交点在无限远处)。那么,当扫描的下标(i)越过了交点之后,先来的决策点就会被踢出去,后来的决策点就比它更优。
样例中,(f_4)和(f_2)的交点的(x)坐标为(frac {17} 4)。这意味着,当(i<frac {17}4)时,(f_2)更优;否则(f_4)更优。
根据上述性质,每个决策点最多会被弹出一次。因此我们可以想到用队列维护决策点集合。对于每个决策点(k),我们处理出它什么时候会被它后面一个决策点弹出去,记为(d_k)。在新扫描到一个位置的时候,我们先将这个位置从队尾加入到决策点集合,并把那些比它劣的决策点全部弹掉。然后再查询当前的答案,先把队头的变劣的决策点弹掉(惰性删除),然后再计算。
时间复杂度(O(nlog_2n))。
代码
#include <cmath>
#include <cstdio>
#include <algorithm>
const int MAXN = 5e5 + 5;
template<typename _T>
void read( _T &x )
{
x = 0;char s = getchar();int f = 1;
while( s > '9' || s < '0' ){if( s == '-' ) f = -1; s = getchar();}
while( s >= '0' && s <= '9' ){x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar();}
x *= f;
}
template<typename _T>
void write( _T x )
{
if( x < 0 ){ putchar( '-' ); x = ( ~ x ) + 1; }
if( 9 < x ){ write( x / 10 ); }
putchar( x % 10 + '0' );
}
template<typename _T>
_T MAX( const _T a, const _T b )
{
return a > b ? a : b;
}
template<typename _T>
_T ABS( const _T a, const _T b )
{
return a > b ? a : b;
}
int q[MAXN], dl[MAXN];
int H[MAXN], p1[MAXN], p2[MAXN];
int N;
double calc( const int j, const int i ) //j < i
{
return H[j] + sqrt( i - j );
}
int lb( const int a, const int b ) //a < b
{
int l = b, r = N, mid, ret = r + 1;
while( l <= r )
{
mid = l + r >> 1;
if( calc( a, mid ) > calc( b, mid ) ) l = mid + 1;
else ret = mid, r = mid - 1;
}
return ret;
}
void calc( int *P )
{
int h = 1, t = 0;
for( int i = 1 ; i <= N ; i ++ )
{
while( h < t && calc( q[t], dl[t - 1] ) < calc( i, dl[t - 1] ) ) t --;
dl[t] = lb( q[t], i ); q[++ t] = i;
while( h < t && i >= dl[h] ) h ++;
P[i] = MAX( P[i], ( int ) ceil( calc( q[h], i ) ) );
}
}
int main()
{
read( N );
for( int i = 1 ; i <= N ; i ++ ) read( H[i] );
calc( p1 );
std :: reverse( H + 1, H + 1 + N );
calc( p2 );
for( int i = 1 ; i <= N ; i ++ )
write( MAX( MAX( p1[i], p2[N - i + 1] ) - H[N - i + 1], 0 ) ), putchar( '
' );
return 0;
}