贪心——Prim算法(避圈法)

1.简介

　　Prim算法是图论中的一种算法，可在带权连通图里搜索产生最小生成树。

　　该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。

　　Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中，在找当前最近顶点时使用到了贪心算法。

　　预备知识(了解的跳过)：

　　无向图、邻接矩阵、最小生成树

2.实例

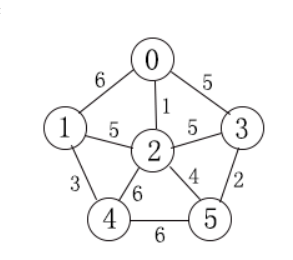
　　先给出一个这样的邻接矩阵，找最小生成树吧：

　　把邻接矩阵可以翻译成这样的无向图：

　　过程：

　　Prim算法是基于节点做优先考虑的，以某一节点开始作为根节点，不断搜索距离的权值最小的节点，然后加入到生成树中。

3.代码

#include<bits/stdc++.h>
#define INF 99999
using namespace std;
const int N = 6;
bool visit[N];
int dist[N] = { 0, };
int graph[N][N] = { {0,6,1,5,INF,INF},  //INF代表两点之间不可达
                    {6,0,5,INF,3,INF},
                    {1,5,0,5,6,4},
                    {5,INF,5,0,INF,2},
                    {INF,3,6,INF,0,6},
                    {INF,INF,4,2,6,0}
                  };
int prim(int cur){
    int index = cur;
    int sum = 0,i = 0,j = 0;
    cout << index << " ";
    memset(visit,false, sizeof(visit));
    visit[cur] = true;
    for(i = 0; i < N; i++)
        dist[i] = graph[cur][i];//初始化，每个与a邻接的点的距离存入dist
    for(i = 1; i < N; i++){
        int minor = INF;
        for(j = 0; j < N; j++){
            if(!visit[j] && dist[j] < minor){   //找到未访问的点中，距离当前最小生成树距离最小的点
                minor = dist[j];
                index = j;
            }
        }
        visit[index] = true;
        cout << index << " ";
        sum += minor;
        for(j = 0; j < N; j++){
            if(!visit[j] && dist[j]>graph[index][j])      //执行更新，如果点距离当前点的距离更近，就更新dist
            {
                dist[j] = graph[index][j];
            }
        }
    }
    cout<<endl;
    return sum;               //返回最小生成树的总路径值
}
int main(){
    cout << prim(0) << endl;//从顶点a开始
    return 0;
}