实验四
实验一
实验内容
- 用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
- 给出伪代码,产品代码,测试代码(不少于5条测试)
实验结果
- 深度遍历
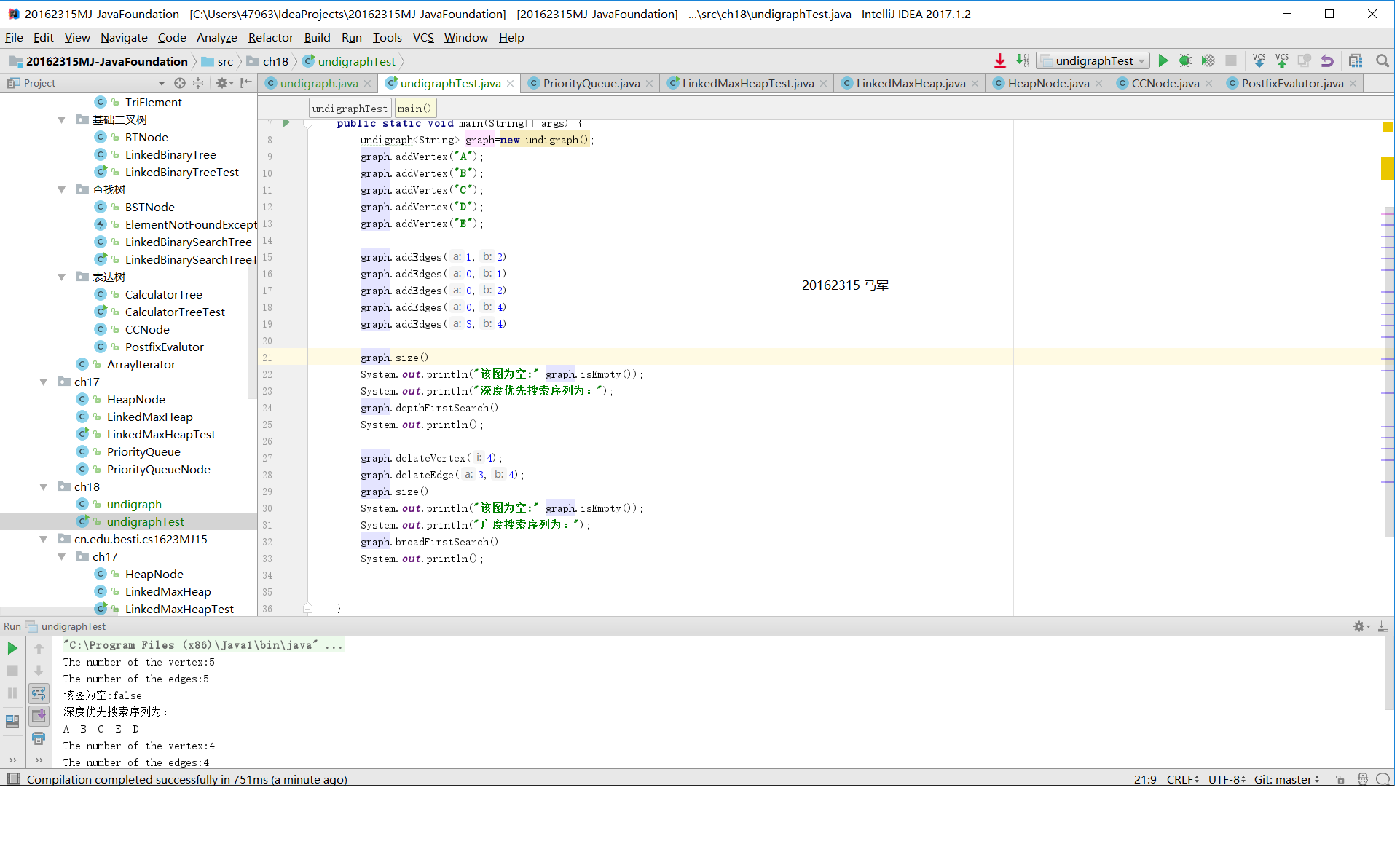
- 广度遍历

实验代码分析
- 该试验要求用邻接矩阵实现无向图,其中包括的方法如要求所列。我创建了一个动态数组vertexlist来储存我所创建的结点。建立了一个二维数组(用以存在边的真假值)。添加删除顶点,返回顶点值方法直接调用动态数组的方法操作,isEmpty只要检测vertexlist是否为空就可以了。
- size方法
public void size(){
System.out.println("The number of the
vertex:"+vertexlist.size());
System.out.println("The number of the
edges:"+edgenumbers);
}
图里面我认为size要返回两个值因此直接写成了void方法把它们打印出来了:顶点的数目和边的数目。
- addEdges方法
public void addEdges(int a,int b){
if (a<vertexlist.size()&&b<vertexlist.size()){
if (adjmatrix[a][b]==1){
System.out.println("The edge has exsisted");
}
adjmatrix[a][b]=1;
adjmatrix[b][a]=1;
edgenumbers++;}
}
在将该边对应的二维数组位置赋值之前首先要检测是否有边,无边时将该位置赋值为1,要注意的是无向图每一条边没有方向,也就是该边的真假对应数组的两个位置。删除边与之同理,将该边的值赋为0就可以解决。
- 遍历的方法
/*int类型方法getNeighbornear(int index)
- 遍历二维数组i行所有路径值
- 返回值为1的列位置
- 寻找失败返回-1*/
public int getNeighbornear(int index) {
for(int c=0;c<vertexlist.size();c++) {
if (adjmatrix[index][c]==1) {
return c;
}
}
return -1;
}
/*int类型方法getNeighbornear(int a,int b )
- 寻找二维数组中a位置元素除b元素外下一个存在路径的顶点
- 寻找失败返回-1*/
public int getNeighborfar(int a,int b) {
for (int c=b+1;c<vertexlist.size();c++) {
if (adjmatrix[a][c]==0) {
return c;
}
}
return -1;
}
遍历方法我没有使用书上的迭代器,在阅读了网上已有的一些代码之后,我学习了很多代码里有的通过设置查找两个邻结点方法来递归进行深广度遍历的方法,这两个方法在接下来进行会引用。
- 深度遍历
public void depthFirstSearch(boolean[] isVisited,int i) {
System.out.print(getVertex(i)+" ");
isVisited[i]=true;/*打印该顶点的值并且将该元素标记为已访问*/
int w=getNeighbornear(i);/*寻找第一个邻结点*/
/*存在第一个邻结点
* 递归进行深度遍历
* 寻找下一个邻结点*/
while (w!=-1) {
if (!isVisited[w]) {
depthFirstSearch(isVisited,w);
}
w=getNeighborfar(i, w);
}
}
/*vodi类型方法depthFirstSearch
* 遍历顶点数组
* 访问每一个顶点并且进行深度遍历*/
public void depthFirstSearch() {
for(int i = 0; i< vertexlist.size(); i++) {
if (!isVisited[i]) {
depthFirstSearch(isVisited,i);
}
}
}
这个方法里面同样设置了顶点是否被访问的这个布尔变量,首先标记第一次访问的顶点,然后如果查找到其第一个邻结点,就继续查找第二个,如果第二个邻结点不存在,那么它就会将第一个邻结点作为初始值重新进行深度遍历的过程。因为前面访问到的顶点都被标记为isVistited,所以不会重复遍历。对所有顶点都进行一次遍历查找邻结点之后就完成了深度遍历,广度遍历与此相似,但使用的是队列进行操作,不再赘述。
实验二
实验内容
-
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
-
给出伪代码,产品代码,测试代码(不少于5条测试)
实验结果

实验代码分析
- 十字链表是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图,可以达到高效的存取效果。同时,代码的可读性也会得到提升。
- 在实现这个代码的过程中我学习了网上的代码,先编写了两个类Vertex顶点类和Edge边类。在这两个类里编写了十字链表必要的元素如弧的出狐点入狐点,同弧头和同狐尾,顶点的出狐和入狐:
public class Edge<E> {
E data;
int fromVertexIndex;
int toVertexIndex;
Edge<E> nextSameFromVertex;
Edge<E> nextSameToVertex;
public Edge(E data, int fromVertexIndex, int toVertexIndex) {
this.data = data;
this.fromVertexIndex = fromVertexIndex;
this.toVertexIndex = toVertexIndex;
}
}
public class Vertex<E,T> {
E data;
Edge<T> firstIn;
Edge<T> firstOut;
public Vertex(E data) {
this.data = data;
}
}
- 关于顶点的增删方法跟动态数组的方法相同并且在测试代码中进行测试了.
-十字链表中重点在于边的添加方法:初始的时候将每个顶点的出入弧都要设置为null,在添加狐之后将结点指针引向与之相连的顶点并寻找同狐头,同狐尾。
public void insertEdge(Edge<Integer> edge, List<Vertex<Integer, Integer>> vertexList) {
int fromVertexIndex = edge.fromVertexIndex;
int toVertexIndex = edge.toVertexIndex;
Vertex<Integer, Integer> fromVertex = vertexList.get(fromVertexIndex);
Vertex<Integer, Integer> toVertex = vertexList.get(toVertexIndex);
if (fromVertex.firstOut == null) {
//插入到顶点的出边属性
fromVertex.firstOut = edge;
} else {
// 插入到edge的nextSameFromVertex属性
Edge<Integer> tempEdge = fromVertex.firstOut;
//找到最后一个Edge
while (tempEdge.nextSameFromVertex != null) {
tempEdge = tempEdge.nextSameFromVertex;
}
tempEdge.nextSameFromVertex = edge;
}
if (toVertex.firstIn == null) {
//插入到顶点的入边属性
toVertex.firstIn = edge;
} else {
// 插入到edge的nextSameToVertex属性
Edge<Integer> tempEdge = toVertex.firstIn;
//找到最后一个Edge
while (tempEdge.nextSameToVertex != null) {
tempEdge = tempEdge.nextSameToVertex;
}
tempEdge.nextSameToVertex = edge;
edgenums++;
}
}
- 在遍历和打印结果的时候通过遍历每个结点,把每条结点的每条弧的都打印出来。
public void traversalandprint(List<Vertex<Integer, Integer>> list) {
for (Vertex<Integer, Integer> vertex : list) {
//输出入度
String infoIn = String.format("vertex: %3d - its in-edge are: ", vertex.data);
Edge<Integer> edge = vertex.firstIn;
while (edge != null) {
infoIn += String.format("(from: %d, to: %d, data: %d)", edge.fromVertexIndex, edge.toVertexIndex, edge.data);
edge = edge.nextSameToVertex;
}
System.out.println(infoIn);
//输出出度
String infoOut = String.format("vertex: %3d - its out-edge are: ", vertex.data);
Edge<Integer> edgeOut = vertex.firstOut;
while (edgeOut != null) {
infoOut += String.format("(from: %d, to: %d, data: %d)", edgeOut.fromVertexIndex, edgeOut.toVertexIndex, edgeOut.data);
edgeOut = edgeOut.nextSameFromVertex;
}
System.out.println(infoOut);
}
实验三
实验内容
- 实现PP19.9:创建计算机网络路由系统,输入网络中点到点的线路,以及每条线路使用的费用,系统输出网络中各点之间最便宜的路径,找出不相通的所有位置。
- 给出伪代码,产品代码,测试代码(不少于5条测试)
实验结果

实验代码分析
要求中最关键的一点就是最短路径,我是通过dijkstra算法实现的:
for (int row = 0; row < edgesMatrix.length; row++) {
for (int column = 0; column < edgesMatrix.length; column++) {
edgesMatrix[row][column] = MAX_VALUE;
}
- 这个项目里的图是带权图,我使用与实验一类似的无反向图实现的,不同的是在初始邻接矩阵的赋值不再是0而是Integer最大值,以无限大来表示没有连接,输入边时多输入一个属性weight,并将weight作为矩阵的值载入。
public boolean addEdge(int vnum1, int vnum2, int weight) {
if (vnum1 >= 0 && vnum2 >= 0 && vnum1 != vnum2 && weight >= 0){
edgesMatrix[vnum1][vnum2] = weight;
edgesMatrix[vnum2][vnum1] = weight;}
return true;
}
- 这个问题的核心是求出顶点间的最短路径,首先确定两点间直接连接长度,然后设置中转点,比较经过中转点的路径长度和直接路径长度来获得最短路径,而在了Dijkstra算法中把结点分成了两类,已经找到了最短路径的顶点标记在一个数组里,其他顶点在另一个数组里继续寻找。
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && edgesMatrix[v][j] < MAX_VALUE) {
if (minDist + edgesMatrix[v][j] <= dist[j]) {
//如果多经由一个v点到达j点的 最短路径反而要短,就更新
dist[j] = minDist + edgesMatrix[v][j];
prev[j] = v; //经由点的序号
}
}
}
- 遍历方式与实验一中的广度遍历类似,不再赘述