廖雪峰Java1-2程序基础-5浮点数运算

1.浮点数运算的特点

• 很多浮点数无法精确表示
• 计算有误差
• 整型可以自动提升到浮点型

如0.1用二进制表示会是一个无限循环的小数。计算机不可能在有限内存中表示一个无限小数。因此浮点数不能精确表示。也造成计算有误差。
如果浮点数和整型进行运算，整型会先提升为浮点型，再进行运算，结果为浮点型。

        double d = 1 - 9.0 /10;//0.09999999999999998
        double d1 = 1.2 + 24.0 / 5;//6.0
        double d2 = 1.2 + 24 / 5;//5.2 整数不会自动提升

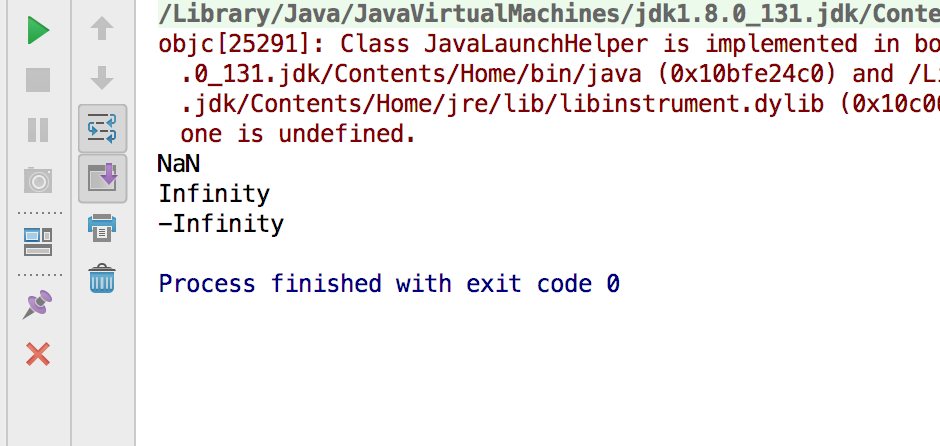
2.特殊值

• NaN表示Not a Number
• Infinity表示无穷大
• -Infinity表示负无穷大

        double d1 = 0.0 / 0;//NaN
        double d2 = 1.0 / 0;//Infinity
        double d3 = -1.0 / 0;//-Infinity
        System.out.println(d1);
        System.out.println(d2);
        System.out.println(d3);

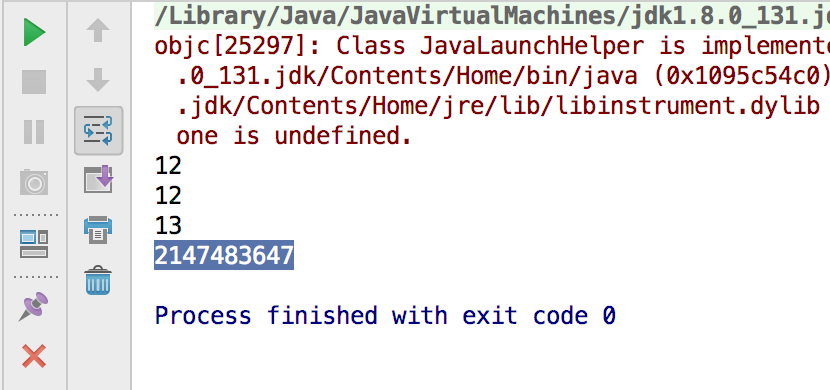
3.强制转型

• 浮点型强制转为整型会直接扔掉小数位
• 四舍五入的技巧，+0.5
• 超出整型范围自动变为最大值

        int n1 = (int)12.3;//12
        int n2 = (int)12.7;//12
        int n3 = (int)(12.7+0.5);//13
        int n4 = (int)1.2e20;//2147483647
        System.out.println(n1);
        System.out.println(n2);
        System.out.println(n3);
        System.out.println(n4);

4.总结：

• 浮点数可能无法精确表示
• 浮点数运算结果可能有误差
• 运算结果会自动提升
• 可以强制转型，但可能丢失精度