#pragma once
#include "stdafx.h"
#include<set>
#include<string>
#include<iostream>
using namespace std;
/*
设计模式-组合模式(Composite)[用类建一棵树]
将对象组合成树形结构以表示 部分-整体 的层次结构。组合模式使得用户对
单个对象和组合对象的使用具有一致性。
*/
class CComponent {//所有节点统一接口
protected:
string m_strName;
public:
CComponent(const string &strName) {
m_strName = strName;
}
virtual void Add(CComponent * const pc) = 0;
virtual void Remove(CComponent * const pc) = 0;
virtual void Display(const int & nDepth) = 0;
};
class CLeaf : public CComponent {
public:
CLeaf(const string &strName) : CComponent(strName) {}
void Add(CComponent *const pc) {
cout << "Cannot add to a leaf" << endl;
}
void Remove(CComponent *const pc) {
cout << "Cannot remove from a leaf" << endl;
}
void Display(const int &nDepth) {
cout << "-" << nDepth << ":" << m_strName << endl;
}
};
class CCpmposite : public CComponent {
private:
set<CComponent*>m_cChildren;
public:
CCpmposite(const string &strName) : CComponent(strName) {
m_cChildren.clear();
}
void Add(CComponent * const pc) {
m_cChildren.insert(pc);
}
void Remove(CComponent * const pc) {
m_cChildren.erase(pc);
delete pc;
}
void Display(const int &nDepth) {
cout << "-" << nDepth << ":" << m_strName << endl;
for each(auto i in m_cChildren) {
i->Display(nDepth + 1);
}
}
~CCpmposite() {
for each(auto i in m_cChildren) {
delete i;
}
}
};
int main() {
CCpmposite *pRoot = new CCpmposite("root");
pRoot->Add(new CLeaf("Lead A"));
pRoot->Add(new CLeaf("Lead B"));
CCpmposite *pComp = new CCpmposite("Composite X");
pComp->Add(new CLeaf("Lead A"));
pComp->Add(new CLeaf("Lead B"));
pRoot->Add(pComp);
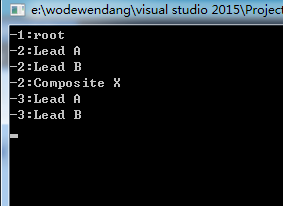
pRoot->Display(1);
delete pRoot;
getchar();
return 0;
}