题目背景
IOI2000第一题
题目描述(题目链接:https://www.luogu.org/problem/P1435)
回文词是一种对称的字符串。任意给定一个字符串,通过插入若干字符,都可以变成回文词。此题的任务是,求出将给定字符串变成回文词所需要插入的最少字符数。
比如 “Ab3bd”插入2个字符后可以变成回文词“dAb3bAd”或“Adb3bdA”,但是插入少于2个的字符无法变成回文词。
注:此问题区分大小写
输入格式
一个字符串(0<strlen<=1000)
输出格式
有且只有一个整数,即最少插入字符数
输入输出样例
输入 #1
Ab3bd
输出 #1
2
题目分析:这道题乍一看与LCS一点关系都没有,但是回文串是正着读和反着读都是一样的,所以就很容易想到将原来的字符串先颠倒过来观察一下
我们先分析下样例:Ab3bd,它的倒序是:db3bA;
你会发现样例的倒序和没倒序之间相同的部分是被b3b,说明它已经是回文不用动,而剩下的(Ad,dA)就是要在其基础上加上(dA,Ad)构成回文,也就是说,添加字母的长度(为构成回文的长度) = 原序列长度-倒序和原序列重叠的长度(已经构成回文的长度);
求重叠的最长长度就用到了LCS
f[i][j]表示串1的i位和串2的j位之前最长公共子序列的长度。
维基百科关于LCS叙述:
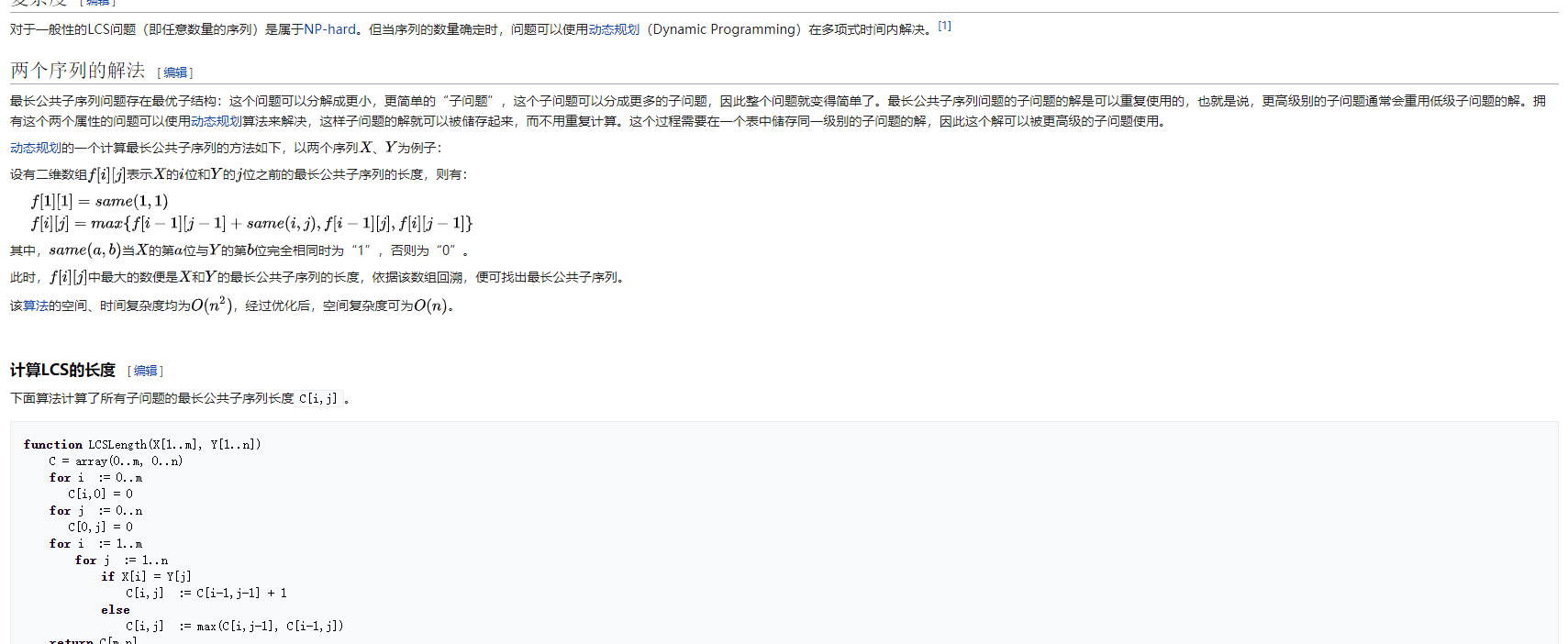
根据LCS模板可以得到以下代码:
#include <bits/stdc++.h> using namespace std; int f[1000+2][1000+2]; int main() { string s,str; int len; cin>>str; len = str.size(); for(int i = 0; i <= len-1; i++) s[i] = str[len-i-1]; for(int i = 0; i<= len-1; i++){ for(int j = 0; j <= len-1; j++){ if(s[i+1] == str[j+1]){ f[i+1][j+1] = f[i][j] + 1; } else{ f[i+1][j+1] = max(f[i][j+1], f[i+1][j]); } } } cout<<len-f[len-1][len-1]; return 0; }