1、矩阵下表引用
|
表达式(Matlab程序) |
函数功能 | |
|---|---|---|
|
1 |
A(1) |
将二维矩阵A重组为一维数组,返回数组中第一个元素 |
|
2 |
A(: , j) |
返回二维矩阵A中第 j 列 列向量 |
|
3 |
A( i , :) |
返回二维矩阵A中第 i 行 行向量 |
|
4 |
A(: , j : k) |
返回二维矩阵A中第 j 列到第 k列 列向量组成的子矩阵 |
|
5 |
A( i : k , :) |
返回二维矩阵A中第 i 行到第 k行 行向量组成的子矩阵 |
|
6 |
A( i : k , j : m) |
返回二维矩阵A中第 i 行到第 k 行 行向量 和第 j 列到第 m 列 列向量的交集组成的子矩阵 |
|
7 |
A(:) |
将二维矩阵A中得每列合并成一个列向量 |
|
8 |
A( j : k) |
返回一个行向量,其元素为A(:)中的第 j 个元素到第 k 个元素 |
|
9 |
A([ j1 j2…]) |
返回一个行向量,其元素为A(:)中的第 j1,j2…个元素 |
|
10 |
A(: , [ j1 j2 …]) |
返回矩阵A的第 j1 列、第 j2 列等的列向量 |
|
11 |
A([ i1 i2 …] : ,) |
返回矩阵A的第 i1 行、第 i2 行等的行向量 |
|
12 |
A([ i1 i2 …] , [ j1 j2 …]) |
返回矩阵A的第 j1列、第 j2 列等和矩阵A的第 i1 行、第 i2 行等的元素 |
下面将常用的几个举例说明:
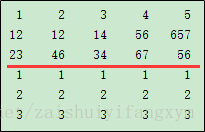
例如:A=[1 2 3 4 5;
12 12 14 56 657;
23 46 34 67 56 ];
(1)将二维矩阵A转化成一维矩阵(列向量):Matlab 默认将其转化成列向量,需要行向量转置即可。
Matlab程序: A(:) %将二维矩阵其转化成列向量
(2)读取矩阵取前N行或N列的方法
Matlab程序:
A(1:2,:) %读取矩阵A前2行
A(:,1:3) %读取矩阵A前3列
(3)求矩阵中每行或每列的最大值和最小值
① 找矩阵A每列的最大值:[max_A,index]=max(A,[],1);
其中,max_A是最大的数值,index是最大的数值所处的位置
② 找矩阵A每行的最大值:[max_A,index]=max(A,[],2);
其中,max_A是最大的数值,index是最大的数值所处的位置
同理可求出每行,每列的最小值。
③ 找矩阵A每列的最小值:[min_A,index]=min(A,[],1);
其中,min_A是最小的数值,index是最小的数值所处的位置
④ 找矩阵A每行的最小值:[min_A,index]=min(A,[],2);
其中,min_A是最小的数值,index是最小的数值所处的位置
2、矩阵合并
已知矩阵:
A=[1 2 3 4 5;
12 12 14 56 657;
23 46 34 67 56];
B=[1 1 1 1 1;
2 2 2 2 2;
3 3 3 3 3];
(1)矩阵A,B左右合并:horzcat(A,B); %矩阵A,B左右合并
(2)矩阵A,B上下合并:vertcat(A,B); %矩阵A,B上下合并
3、矩阵运算(加、减、乘、除、点乘、点除等)
(1)A+B; 表示矩阵A和矩阵B相加(各个元素对应相加);
(2)A-B; 表示矩阵A和矩阵B相减(各个元素对应相减);
(3)A*B; 表示矩阵A和矩阵B相乘;
(4)A.*B; 表示矩阵A和矩阵B对应元素相乘(点乘);
(5)A/B; 表示矩阵A与矩阵B相除法;
(6)A./B; 表示矩阵A和矩阵B对应元素相除(点除);
(7)A^B; 表示矩阵A的B次幂;
(8)A.^B; 表示矩阵A的每个元素的B次幂。
Matlab平台提供了大量的运算函数,很强势。下面列举了常用的函数
|
函数 |
运算法则 | |
|---|---|---|
|
1 |
exp(x) |
求以e为底数的x次幂 |
|
2 |
log(x) |
求以e为底数对x值取对数 |
|
3 |
Log10(x) |
求以10为底数x值取对数 |
|
4 |
sqrt(x) |
求x的平方根 |
|
5 |
sin(x) |
正弦函数 |
|
6 |
cos(x) |
余弦函数 |
|
7 |
tan(x) |
正切函数 |
|
8 |
asin(x) |
反正弦函数 |
|
9 |
acos(x) |
反余弦函数 |
|
10 |
atan(x) |
反正切函数 |
|
11 |
mode(a,b) |
a与b相除取余数 |
|
12 |
min(a,b) |
返回a, b中较小的数值 |
|
13 |
max(a,b) |
返回a, b中较大的数值 |
|
14 |
mean(x) |
求x的列平均数(列平均) |
|
15 |
median(x) |
求x的列中位数(列中位数) |
|
16 |
sum(x) |
x中各个列之间的元素求和 |
|
17 |
rank(x) |
X矩阵的秩 |