
training set 训练集 validation set 验证集 test set测试集 这些与衡量你做的怎么样有关
当你知道怎么衡量你在一个问题的表现,问题就解决了一半。(衡量表现的重要性)

每个你将建立的分类器都会尝试记住训练集,并且它通常在这方面会做的很好很好
你的工作 是帮助它泛化到新的数据上
所以我们怎么用测量泛化能力代替测量分类其记住数据的能力
最简单的方法就是从训练集中取出一个小的子集

现在用它训练和测量测试数据上的错误,问题解决了,你的分类器现在不能欺骗你了
因为它从未见过测试数据,所以它不可能记住数据
但仍然有一个我呢提,因为训练一个分类器通常是一个反复试错的过程
你尝试一个分类器 测量它的性能,你尝试另一个,再测量,再另一个,再另一个
你调整这个模型,探索参数,测量
最终 你得到了你认为完美的分类器,最后你小心的把测试数据从训练数据中分离
并且只测量在测试数据上的性能
现在你在一个真实的生产环境中部署你的系统,你得到了更多的数据,你在新数据上给性能打分
它几乎做不好,可能发生了什么呢?
发生的是: 你的分类器已经通过你的眼睛,间接地看到了测试数据
每次你决定用哪个分类器时, 调整哪个参数时,你确实给了分类器测试集的信息
只有一点点,但它加起来,所以随着时间的流逝 随着你进行很多次很多次实验
你的测试数据渗透进你的训练数据

所以我们能做什么? 有很多方法可以解决这个问题,这里给一个最简单的

从你的训练集里再取出一部分,把它藏起来,不要看它直到你做出了最后的决定
你可以用你的验证集去测量实际误差,可能验证集会渗透进训练集,但是那没有关系
因为你最总是有这个测试集的,你可以依靠它去实际测量真正的性能
过拟合与数据集大小
在这里不讨论交叉验证,但是如果在你的课程中从未遇到,强烈建议你去学习它,交叉验证是深度学习的关键
深度学习有很多旋钮你可以调节,你将会一遍又一遍的调整他们,
你要小心在你的测试集上过拟合,用验证集,你的验证集和测试集需要多大呢?
视情况而定,你的验证集越大,你的数会越精确

想像一下你的验证集只有六个实例 精确度为66%
现在你调整你的模型,性能从66%提升到83%,这些可信吗?
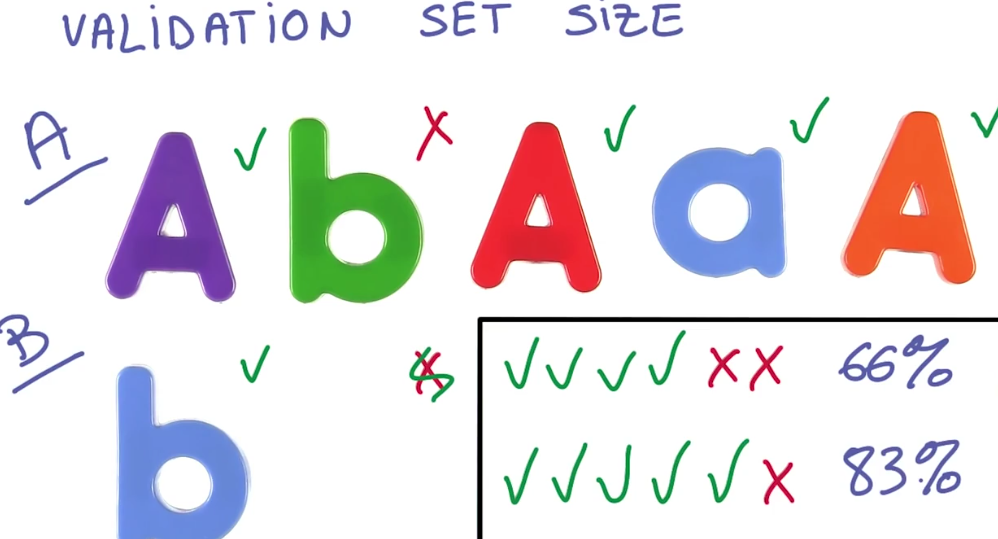
当然不能,这只是一个实例的标签改变了,它可能只是噪声
你的测试集越大 噪声越少 测量越准确

这是个很有用的经验法则

在你的验证集上影响了30个实例的改变,这样或那样的方式
通常是有统计学意义的,通常是可以信任的

想象你的验证集里有3000个实例,假定你信任30的规则,你可以相信哪个水平的准确性的提升?

当你得到从80%到81%这1%的提升,更有说服力 有30个实例从不正确到正确
这是个很强大的信号 不论你在做的是什么 确实提升了你的准确率

这是为什么对大多数分类器任务,人们倾向于用超过3000个实例做验证集,
这使得准确率的第一个小数位是有效数字,给你足够的分辨率去看到小的改进
如果你的类是不平衡的 例如
如果一些重要的类别很罕见 它的启发式就不再是好的
坏消息 你只需要更多的数据

现在 如果你的训练集很小 分出3000个实例也是很多的数据,我们之前提过的交叉验证
是一个可能的方法来缓解这个问题,但是交叉验证可能是一个漫长的过程
因此获得更多的数据往往是正确的解决方法
对逻辑分类器做最优化
回到训练模型上来,利用梯度下降法训练逻辑回归非常有效
一方面 你是直接优化你所关心的误差 这是个非常棒的主意
这就是为什么在应用时 许多机器学习的研究工作 都是关于设计好的损失函数,用于做最优化。
但正如你在作业中运行模型时可能遇到的那样,它存在最大的问题是它非常难以规模化
随机梯度下降法

解决梯度下降算法 难以 规模化的问题很简单,你要计算这个梯度
这里有一个经验法则:如果计算这个操作需要n次浮点运算,那么计算这个梯度则需要三倍计算量
正如之前那样,损失函数非常巨大,它取决于你数据集的没一个元素
如果你的数据集较大 那会是非常打的计算量,但我们期望能训练大量的数据,因为实际问题中
有更多的数据总会有更多的收获 因为梯度下降比较直接,要实现它需要很多步
这意味着你要遍历的整个数据集上百次,这并不好,因此我们打算偷个懒

与其计算损失 还不如直接计算它的估计值,一个非常差的估计,实际上是差的惨不忍睹
这个估计差到你会怀疑为啥它还能有效,但这样就是可行,
因为我们又花了时间让它没那么差。我们将要使用的估计值是随机从数据集中抽取的很小一部分的平均损失
一般在1到1000个样本左右,说到 随机 因为这非常重要,如果你选样本时不够随机
那它就完全不再有效,因此我们将取出数据集中非常小的一片,计算那些样本的损失和导数
并假设那个导数就是进行梯度下降正确的方向。
它并不是每次都是正确的方向,实际上它偶尔还会增加实际的损失,而不是减少它,
但我们通过每次执行非常非常小的步幅,多次执行这个过程来补偿它
因此每一步变得更容易计算,但我们也付出了代价,相比于一大步,我们需要走很多小步
总的来说我们还是赢了好多。事实上,相比于梯度下降,这样做异常有效

这种技术便叫做随机梯度下降,这是深度学习的核心
因为随机梯度下降在数据和模型尺寸方面扩展性很好,我们期望同时有大量的数据和大模型
随机梯度下降 简称 SGD 则非常棒且容易规模化
但由于它本质上是一个非常差的优化器,碰巧它又是唯一足够快的
实际中能解决很多问题
动量法与使用学习率调节下降

之前让输入零均值同方差,这对SGD很重要,用方差较小的随机权重来进行初始化。
下面学习更多重要的技巧,这应该包括了实现SGD所需要的所有技巧

第一个是动量(momentum)
回忆一下 在SGD里,虽然我们每次只是往随机方向走一小步
但积累起来,就能带我们来到损失函数的极小值处
其实,先前走过的步子还积累了关于前进方向的知识,我们也可以把这方面知识利用起来

一个省事的方式是保持梯度的移动平均,用移动平均代替当前一批数据的方向
这种动量技术很有效 常常会有更好的收敛性

第二个是学习率衰减
回忆一下 用SGD代替梯度下降时,在接近目标的时候 我们的步子要走的更小和更有噪声,多小的步子呢?
这其实也是个研究领域,不过 步子随着不断训练而越来越小,这样做总是有好处的
有些人喜欢用学习率的指标衰减 有些人喜欢每当损失到达停滞时变小 方法很多
但要记住的关键一点,是随着时间流逝而减小它的值
超空间参数

调整学习率常常让人觉得奇怪,比如 你可能认为更高的学习率代表你能学习更多,或者学得更快
但这并不是真的。事实上 如果你在训练模型的时候降低学习率,能够更快地得到一个更好的模型
它也可能变得更糟,你也许会希望通过观察损失曲线,得知模型的训练速度
越高的学习率在开始的时候学的很快,但是过了一会就会放缓了
而较低的学习率能让模型继续训练并变得更好
这张图对于每一个训练神经网络的人来说都非常熟悉,永远不要相信模型的训练速度
这和你的模型训练的有多好基本没有关系

这也是为什么人们认为SGD是黑魔法
你还有很多超参数可以调节:
初始化权重(initialization parameters)
学习率(learning rate parameters)
衰减比(decay)
动量(momentum)
并且你要确保他们 是正确的
在实际训练的时候 情况会好很多
但是还是要记住一件事情,当训练出现问题的时候,首先应该想到 降低学习率

对于小模型来说还有很多好的解决办法,遗憾的是 目前还没有一个让人完全满意的非常大的模型。
我们将会介绍一个AdaGrad模型 能够让事情变得简单一点。
AdaGrad是SGD的优化版本,它使用了动量来防止过拟合,而且学习率能够自动衰减
使用AdaGrad能够降低训练过程对超参数的敏感度,但是它的准确率比使用动量的SGD低一些
如果你只是希望它能够使用,AdaGrad仍然是一个非常好的选择
概括一下:
我们有一个非常简单的线性模型 它可以计算概率,我们也可以用它来进行分类
我们现在知道该如何在大量的数据之上,使用SGD之类的算法优化它的参数
尽管它只是一个简单的线性模型,现在我们已经有了我们需要的所有的工具,是时候去进行更深入的学习了
