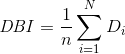Clustering metrics 聚类评价指标

Clustering metrics

See the Clustering performance evaluation section of the user guide for further details.

The sklearn.metrics.cluster submodule contains evaluation metrics for cluster analysis results. There are two forms of evaluation:

• supervised, which uses a ground truth class values for each sample.

• unsupervised, which does not and measures the ‘quality’ of the model itself.

metrics.adjusted_mutual_info_score(…[, …])	Adjusted Mutual Information between two clusterings.
metrics.adjusted_rand_score(labels_true, …)	Rand index adjusted for chance.
metrics.calinski_harabasz_score(X, labels)	Compute the Calinski and Harabasz score.
metrics.davies_bouldin_score(X, labels)	Computes the Davies-Bouldin score.
metrics.completeness_score(labels_true, …)	Completeness metric of a cluster labeling given a ground truth.
metrics.cluster.contingency_matrix(…[, …])	Build a contingency matrix describing the relationship between labels.
metrics.fowlkes_mallows_score(labels_true, …)	Measure the similarity of two clusterings of a set of points.
metrics.homogeneity_completeness_v_measure(…)	Compute the homogeneity and completeness and V-Measure scores at once.
metrics.homogeneity_score(labels_true, …)	Homogeneity metric of a cluster labeling given a ground truth.
metrics.mutual_info_score(labels_true, …)	Mutual Information between two clusterings.
metrics.normalized_mutual_info_score(…[, …])	Normalized Mutual Information between two clusterings.
metrics.silhouette_score(X, labels[, …])	Compute the mean Silhouette Coefficient of all samples.
metrics.silhouette_samples(X, labels[, metric])	Compute the Silhouette Coefficient for each sample.
metrics.v_measure_score(labels_true, labels_pred)	V-measure cluster labeling given a ground truth.

---

 

聚类算法评价指标——Davies-Bouldin指数(Dbi)

    最近在做一个时空序列聚类的小项目，度量聚类优劣的指标使用到了DBI指数，所以开始学习了一下DBI指数，以下是我的理解和基于python3的实现：

    戴维森堡丁指数(DBI)，又称为分类适确性指标，是由大卫L·戴维斯和唐纳德·Bouldin提出的一种评估聚类算法优劣的指标。首先假设我们有m个时间序列，这些时间序列聚类为n个簇。m个时间序列设为输入矩阵X，n个簇类设为N作为参数传入算法。使用下列公式进行计算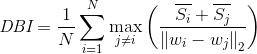：这个公式的含义是度量每个簇类最大相似度的均值。

    接下来是算法的具体计算步骤：

    1、计算Si

    DBI计算公式中首先定义了Si变量，Si计算的是类内数据到簇质心的平均距离，代表了簇类i中各时间序列的分散程度，计算公式为：其中Xj代表簇类i中第j个数据点，也就是一个时间序列，Ai是簇类i的质心，Ti是簇类i中数据的个数，p在通常情况下取2，这样就可以计算独立的数据点和质心的欧式距离（euclidean metric），当然在考察流型和高维数据的时候，欧氏距离也许不是最佳的距离计算方式，但也是比较典型的了。

    2、计算Mij

    分子之和计算完后，需计算分母Mij，定义为簇类i与簇类j的距离，计算公式为：

a_{k,i代表簇类i质心点的第k个值，Mij就是簇类i与簇类j质心的距离。}

    3、计算Rij

    计算了分子与分母后，DBI定义了一个衡量相似度的值Rij，计算公式为：

    4、计算DBI

    有了以上公式的基础，我们做一个基于簇类数n的n^2的嵌套循环，对每一个簇类i计算最大值的Rij，记为Di，即，也即簇类i与其他类的最大相似度值，也就是取出最差结果。然后对所有类的最大相似度取均值就得到了DBI指数，计算公式为：

---

 

聚类︱python实现 六大 分群质量评估指标（兰德系数、互信息、轮廓系数）

之前关于聚类题材的博客有以下两篇： 
1、 笔记︱多种常见聚类模型以及分群质量评估（聚类注意事项、使用技巧） 
2、k-means+python︱scikit-learn中的KMeans聚类实现 
.

---

1 R语言中的分群质量——轮廓系数

因为先前惯用R语言，那么来看看R语言中的分群质量评估，节选自笔记︱多种常见聚类模型以及分群质量评估（聚类注意事项、使用技巧）：

没有固定标准，一般会3-10分群。或者用一些指标评价，然后交叉验证不同群的分群指标。 
一般的指标：轮廓系数silhouette（-1,1之间，值越大，聚类效果越好）（fpc包），兰德指数rand；R语言中有一个包用30种方法来评价不同类的方法（NbClust），但是速度较慢 
商业上的指标：分群结果的覆盖率；分群结果的稳定性；分群结果是否从商业上易于理解和执行 
轮廓系数旨在将某个对象与自己的簇的相似程度和与其他簇的相似程度进行比较。轮廓系数最高的簇的数量表示簇的数量的最佳选择。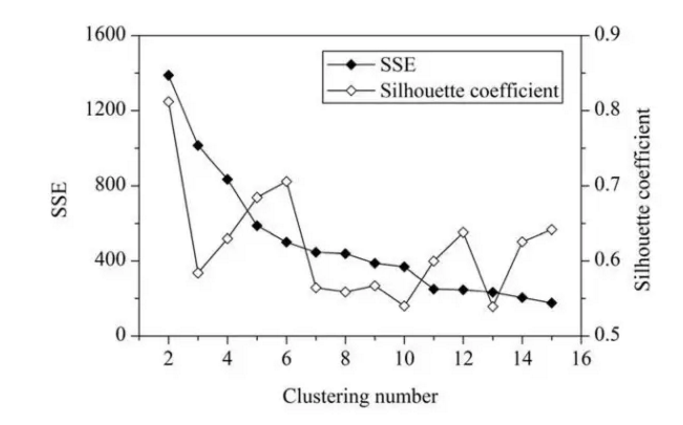 
一般来说，平均轮廓系数越高，聚类的质量也相对较好。在这，对于研究区域的网格单元，最优聚类数应该是2，这时平均轮廓系数的值最高。但是，聚类结果（k=2）的 SSE 值太大了。当 k=6 时，SEE 的值会低很多，但此时平均轮廓系数的值非常高，仅仅比 k=2 时的值低一点。因此，k=6 是最佳的选择。 
.

---

2 python中的分群质量

主要参考来自官方文档：Clustering

部分内容来源于：机器学习评价指标大汇总 
个人比较偏好的三个指标有：Calinski-Harabaz Index（未知真实index的模型评估）、Homogeneity, completeness and V-measure（聚类数量情况）、轮廓系数

1.1 Adjusted Rand index 调整兰德系数

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.adjusted_rand_score(labels_true, labels_pred)  
0.24

• 1
• 2
• 3
• 4
• 5
• 6

.

1.2 Mutual Information based scores 互信息

Two different normalized versions of this measure are available, Normalized Mutual Information(NMI) and Adjusted Mutual Information(AMI). NMI is often used in the literature while AMI was proposed more recently and is normalized against chance:

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)  
0.22504

• 1
• 2
• 3
• 4
• 5
• 6

.

1.3 Homogeneity, completeness and V-measure

同质性homogeneity：每个群集只包含单个类的成员。 
完整性completeness：给定类的所有成员都分配给同一个群集。

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.homogeneity_score(labels_true, labels_pred)  
0.66...

>>> metrics.completeness_score(labels_true, labels_pred) 
0.42...

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

两者的调和平均V-measure：

>>> metrics.v_measure_score(labels_true, labels_pred)    
0.51...

• 1
• 2

.

1.4 Fowlkes-Mallows scores

The Fowlkes-Mallows score FMI is defined as the geometric mean of the pairwise precision and recall: 

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>>
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)  
0.47140...

• 1
• 2
• 3
• 4
• 5
• 6

.

1.5 Silhouette Coefficient 轮廓系数

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
...                                                      
0.55...

• 1
• 2
• 3
• 4
• 5
• 6
• 7

.

1.6 Calinski-Harabaz Index

这个计算简单直接，得到的Calinski-Harabasz分数值ss越大则聚类效果越好。Calinski-Harabasz分数值ss的数学计算公式是（理论介绍来源于：用scikit-learn学习K-Means聚类）：

　

也就是说，类别内部数据的协方差越小越好，类别之间的协方差越大越好，这样的Calinski-Harabasz分数会高。 
　在scikit-learn中， Calinski-Harabasz Index对应的方法是metrics.calinski_harabaz_score. 
在真实的分群label不知道的情况下，可以作为评估模型的一个指标。 
同时，数值越小可以理解为：组间协方差很小，组与组之间界限不明显。 
与轮廓系数的对比，笔者觉得最大的优势：快！相差几百倍！毫秒级

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabaz_score(X, labels)  
560.39...