Python 调C 示例《采样方法总结：Alias method》

采样方法总结：Alias method

之前做的论文中，有一处关键的计算涉及到对一个高维度的离散分布求数学期望，这个问题本来可以简单地sum over这个概率分布的support解决，然而这个方案被reviewer质疑运行速度太慢，于是又想出一招用alias method做Monte Carlo采样算积分。用了采样以后程序变得更容易并行化，用C写了下效率大增。由于网上已经有相当多介绍alias method采样方法的文章了，其中不少还非常详细，我再写一遍也不过鹦鹉学舌，因此本文只对实现方法作简单记录。

相关链接：

一个国外大神写的文章，介绍非常详细：Darts, Dice, and Coins；

一篇讲得简单清晰的中文文章：【数学】时间复杂度O(1)的离散采样算法-- Alias method/别名采样方法；

C++实现：https://oroboro.com/non-uniform-random-numbers/；

各种离散采样方法的实验比较：回应CSDN肖舸《做程序，要“专注”和“客观”》，实验比较各离散采样算法 - Milo Yip - 博客园；

Naive Implementation:

最早写的这个版本应该是网上所有alias method实现里代码量最少，也最简单暴力的版本了，虽然复杂度并不是最优。

注意：

• 为了方便在Python中调用，这里把生成alias table的过程写在cpp中，在Python里用numpy的C++接口调用cpp；
• 因为这个实现过于简单暴力，两种情况下代码会死循环，第一是输入的pdf不合法的情况，即pdf向量中所有元素加起来不等于1.0，第二是浮点数精度不足带来的条件判断不通过问题，这里的代码在我的电脑上运行良好；

用shell（或用 python 调shell ）跑咩？

// TO COMPILE sampler.cpp into sampler.so:
// g++ -std=c++11 sampler.cpp -o sampler.so -shared -fPIC -O2 -D_GLIBCXX_USE_CXX11_ABI=0

extern "C" {
/**
* @brief	Generate an alias table from a discrete distribution
* @param	out		An array of size 2 * length, representing the alias table
Note that this array should be 1.0 in each column after the function
**/
void gen_alias_table(float* out, int* events, int length) {
	int more, less, flag;
	while (true) {
		flag = 1;
		for (int i = 0; i < length; i++) {
			if (out[i] + out[i + length] < 1.0) {
				less = i;
				flag = 0;
				break;
			}
		}
		for (int i = 0; i < length; i++) {
			if (out[i] + out[i + length] > 1.0) {
				more = i;
				flag = 0;
				break;
			}
		}
		if (flag)
			break;
		out[less + length] = 1.0 - out[less];
		out[more] = out[more] - 1.0 + out[less];
		events[less + length] = more;
	}
}
} // extern "C"

Python部分实现如下：

# utils.py
import numpy as np
import ctypes as ct

class discreteSampler(object):
    def __init__(self, probs):
        '''
        This class can sample from high dimensional discrete distribution using the Alias method
        For better efficiency, the generation of alias table is implemented with C++
        :param probs: a 1 dimensional numpy.ndarray representing the PDF for the discrete distribution
        '''
        length = probs.shape[-1]
        self.probs = np.copy(probs)
        self.alias = np.zeros((2, length), dtype=np.float32)
        self.alias[0, :] = self.probs * length
        self.events = np.ones((2, length), dtype=np.int32)
        self.events[0, :] = np.arange(0, length, dtype=np.int32)
        self.events[1, :] = -1.0

        # Load and run the C++ dynamic library
        BASE_DIR = os.path.dirname(os.path.abspath(__file__))
        self.dll = np.ctypeslib.load_library(os.path.join(BASE_DIR, 'sampler.so'), '.')
        self.dll.gen_alias_table(self.alias.ctypes.data_as(ct.c_void_p),
                                 self.events.ctypes.data_as(ct.c_void_p),
                                 ct.c_int(length))

    def generate(self):
        idx = random.randint(0, self.probs.shape[-1] - 1)
        if random.uniform(0.0, 1.0) <= self.alias[0, idx]:
            return idx
        else:
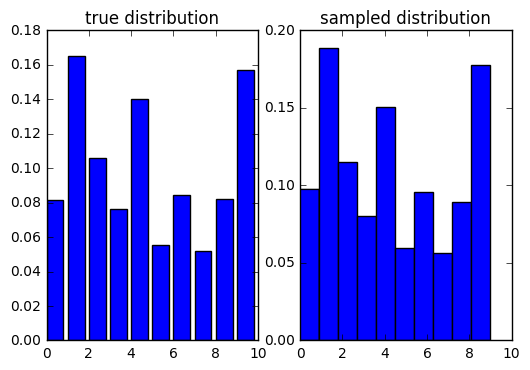
            return self.events[1, idx]

最后用随机数测试下，采样10000次，可视化。

# Testing the sampling using the alias method implementation
import numpy as np
import utils
import matplotlib.pyplot as plt

probs = np.random.uniform(0.0, 1.0, [10])
probs /= np.sum(probs)
idxs = np.arange(0, 10)

sampler = utils.discreteSampler(probs)
collect = list()
for it in range(10000):
    collect.append(sampler.generate())
    
plt.figure()
plt.subplot(121)
plt.bar(idxs, probs)
plt.title('true distribution')
plt.subplot(122)
plt.hist(collect, bins=10, normed=True)
plt.title('sampled distribution')
plt.show()

运行结果：