替代梯度下降——基于极大值原理的深度学习训练算法
在深度学习中，基于梯度下降的算法是目前最主流的参数优化方法，例如SGD，Adam等等，不过这次介绍的论文就提出了另外一种用来训练神经网络参数的方法。先简单概括一下，论文的核心思想是将神经网络看作是一个动力学系统，而把对网络的训练过程看作是如何实现对这个动力学系统的最优控制，按照这样的思路，作者基于庞特里亚金极大值原理（Pontryagin's maximum principle, PMP）设计了一个迭代算法，来求得这个控制问题的最优解，从而实现对于神经网络参数的优化。
神经网络—>动力学系统
其实将神经网络看作动力学系统的想法并不新鲜，尤其是当残差网络（residual network, ResNet）提出以后，这一观点变得更加流行。简单来说，ResNet可以看作是动力学系统的离散时间近似，具体描述可以接着看下文。
对于监督学习来说，其目的就是通过神经网络来去逼近一个从X映射到Y的函数 ，其中X就是输入的样本数据，而Y就是对应的目标值。假设样本特征有d维，一共K个样本，则有样本集
，其中
。
现在通过动力学的观点来看神经网络，我们认为输入X就是运动物体的初始状态，比如粒子的位置。在我们的动力学系统中，这些粒子遵循下面的规律运动：
其中t代表时间， 代表该系统在t时刻的参数，而
代表位置X对时间的导数，即速度。
这就是一个给定初始状态的常微分方程，求解该方程，我们就可以得出粒子的最终状态
现在将时间离散化，为了得出最终状态 ，可以通过前向欧拉法求解：
通过上式可以看出，残差网络中的第n层就可以看作是其中的函数 ，每一层的输出
都是该层输入
加上函数
的计算结果
乘一个常数
。因此我们可以将ResNet看作一个动力学系统。
方便起见，我们还是先讨论时间连续的情况，对于最终状态，可以计算它的loss
，其中函数
是固定的，因此优化问题就可以写成如下形式：
其中 是参数空间，
在控制问题中叫做running cost，放在机器学习中可以理解为是一个正则化项。
而这篇论文的核心内容就是对这个优化问题进行求解。
为了简便起见，之后的讨论认为样本数K=1，而这并不会影响最终的结论。
Pontryagin's maximum principle
论文中采用了庞特里亚金极大值原理(Pontryagin's maximum principle, PMP)的思想来求解优化问题，具体方法如下：
首先定义哈密顿量H
那么PMP就告诉我们，下列条件：
(1)
(2)
(3)
就是上述优化问题最优解的必要条件，注意到这里只是必要条件，也就是说PMP得到的不一定是全局最优解，不过在实际情况中，PMP的解通常已经足够好了。
在上述条件中， 叫做协态(co-state)，而
就是我们想要的最优控制参数，也就是神经网络的最优参数。通过条件(3)可以看出，这其实是一个很强的条件，一般的条件都是梯度为0(
)等形式，而条件(3)则直接保证了H的全局最大，这样做的好处就是参数空间
可以不是连续可微的，即使
是一些离散值的集合，PMP依然可以成立。
Method of Successive Approximations
- Basic MSA
想要通过PMP得到最优解，就需要同时得到满足条件的 ，想要得到这些解的解析形式是很困难的，因此论文中采用了逐次逼近法( Method of Successive Approximations, MSA)来求得数值逼近解，MSA是一种通过交替进行传播与优化来迭代求解的方法，具体步骤如下：
Basic MSA算法
首先第一步是根据条件(1)计算 ，原方程
可以化简为
；已知初始条件
，通过常微分方程解出
后，通过
求得T时刻的协态
作为末状态，然后再通过常微分方程
解出
；得到
和
之后，就可以寻找令哈密顿量H最大的参数
，完成一次迭代，这样迭代多次之后，我们就可以得到满足精度要求的最优解
，这就是Basic MSA的具体步骤。
整体来看，MSA其实可以被分为两大部分：前向-后向哈密顿动力学( forward-backward Hamiltonian dynamics)以及控制参数的最大化。先是通过前向传播求出 ，然后再通过后向传播得到
，最后实现对于控制参数
的最大化。这里有一个非常值得注意地方，那就是哈密顿量H的最大化是与时间解耦(decoupled)的，这也就是说我们可以分别对t进行最大化，从神经网络的角度来看，这就意味着我们可以让不同的网络层并行地执行参数最大化操作。相比于
和
的前向-后向传播，
的最大化往往更加耗费时间，因此该算法的这个特点可以显著地提高速度。
尽管看起来很好，但是Basic MSA却有一个问题，那就是它没有办法保证一定收敛到最优解，如果迭代的初始参数 选择得不好，那么就会导致结果出现偏差。
2. 误差估计
现在就来分析一下到底是哪里导致Basic MSA出现了偏差，回忆一下，需要优化的问题是：
而我们要做的就是 ，首先给出一些前提假设：
有了这些假设，就可以得到如下的结论（具体证明可看原论文的附录B）：
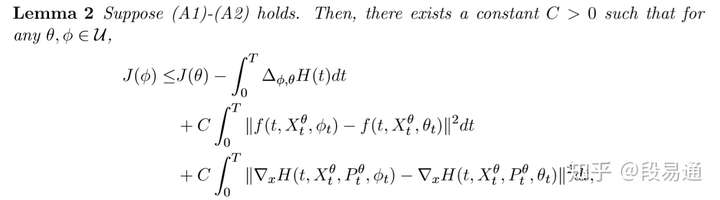
其中 和
满足之前的条件
而lemma中的
从上面的不等式可以看出，要想使得 ，那么仅仅令
是不够的，还应该考虑不等式右边的后两项，它们可以被解释为用参数
替代
后，新哈密顿方程对于原方程产生的误差，换句话说它们反映了替换参数后的方程对原来状态的满足性，因此把它们叫做可行性误差( feasibility errors)。若可行性误差过大，则Basic MSA就有可能出现收敛的偏差。
3.Extended PMP and Extended MSA
为了确保PMP的收敛性，就需要控制可行性误差的大小，因此论文提出了Extended PMP和相应的Extended MSA，它参考了增广拉格朗日方法，将哈密顿量的形式变为：
那么就有Extended PMP：
上面的公式成立是优化问题最优解的必要条件，Extended PMP的证明也很简单，若 是最优参数，则由PMP可知
则Extended PMP的哈密顿量变为
形式与PMP的哈密顿量一样，因此Extended PMP的三个条件也同样可被满足，所以Extended PMP的条件同样是最优解的必要条件。可以看出，因为Extended PMP是由PMP推出来的，它的成立需要建立在PMP成立的基础上，所以Extended PMP其实一个比PMP更弱的必要条件，而构建它的目的就是为了控制可行性误差。
有了Extended PMP以后，就可以得到相应的Extended MSA，其算法流程如下：
E-MSA
其实从算法流程中可以注意到，迭代的前两步相较于Basic MSA并没有发生变化，这是因为当 时，有
形式与Basic MSA一致，因此Extended MSA的前两步无需变化（这一点可能会有些不好理解，如果不明白，可以将这个E-MSA仍看作是Basic MSA，只不过第三个条件中的 换成了
，反正它们都是最优解的必要条件，因此算法仍然成立）。
现在来证明Extended MSA可以解决上述的可行性误差问题，首先定义
由算法可知（注意上标k和k+1）
对不等式从0到T积分，则有
考虑到本轮迭代的前两步已经满足
则有
将这个式子与lemma 2进行对比，可以发现只要选择一个合适的 ，它就可以保证
会随着迭代不断减小
现在分析一下这个不等式，不等式的右侧的后两项一定小于等于0，因此 一定大于等于0，这也就说明了每一轮迭代
的一直在变大。如果
不再增加，即
趋近于0时，那么后两项就一定也会趋近0，即可行性误差收敛为0，也就是说更新参数后的哈密顿量仍然可以满足原状态。
现在证明，当 足够大时，
一定会收敛于0，如下所示。
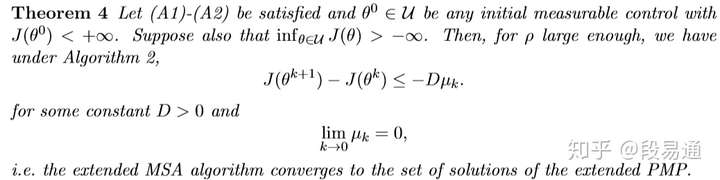
时间离散化表示
- Discrete-Time PMP and Discrete-Time MSA
前面的讨论都是基于连续时间的情况，这与动力学系统的特性相符合，不过前面也已经提到了，神经网络应该被看作是离散时间下的动力学系统，因此我们还需要得到上面算法的时间离散化版本。
再回顾一下，时间离散化后，我们可以通过前向欧拉法求解状态X，即
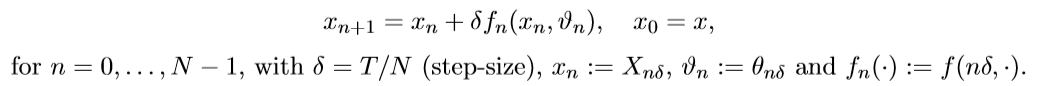
相应地，原先的最优化问题就变为
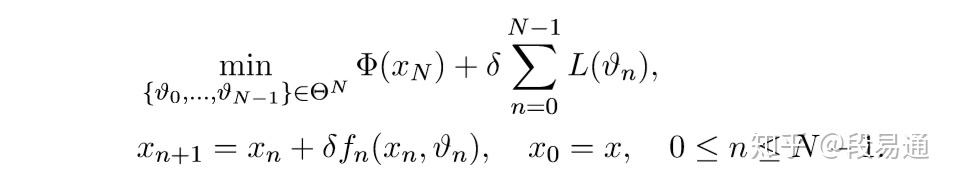
定义离散哈密顿量
则离散时间版本的PMP为：
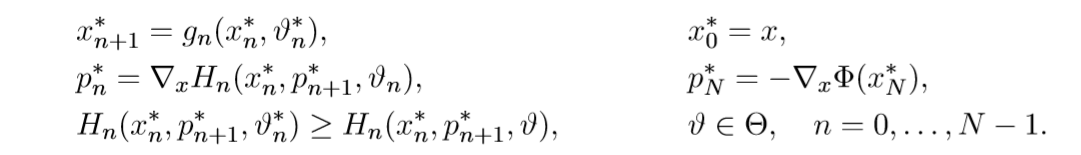
其中
看到这里我们可能会产生一个疑问，那就是上面连续时间的结论在离散化后还成立吗？不幸的是，答案是不一定，已经有一些研究结果表明PMP对于一些离散时间的动力学系统并不成立，这篇论文并没有给出PMP仍适用的证明，作者只是希望在一些适当的情况下，lemma 2对于离散情况还能够成立。
最后给出E-MSA的离散版本
图中画红线的地方估计是作者写错了，应该是
简单说一下流程，其实和连续情况很相似，离散版本中给定x的初始状态，通过前向欧拉法求得x的数值解，然后计算出p的末状态，然后用反向欧拉法得出p的解；最后最大化哈密顿量，完成一次迭代。
2. 与梯度下降的关系
作为一种替代梯度下降的方法，我们肯定要对MSA和梯度下降进行比较，而这篇论文则证明了梯度下降只是Basic MSA在一些特殊情况下的结果。
现在回到Basic MSA，我们修改一下迭代中最后一步的哈密顿量最大化操作，让它变“软”一点
对于这样的Basic MSA，它与梯度下降等价，证明如下
因此，梯度下降就可以看作是Basic MSA的“软化”版本，它与Basic MSA的差别就在于迭代的最后一步，由于需要求参数的梯度，因此梯度下降要求损失函数对于参数是可微的，而由于MSA方法并不需要考虑求参数的梯度，因此它对于参数空间的要求更低。
3. Mini-batch Algorithms
还记得刚开始的时候，为了方便我们令样本数K=1吗？现在就可以把结论拓展到mini-batch上了，结果如下：
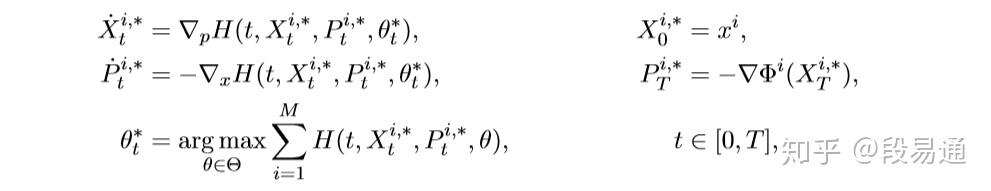
对于MSA，迭代前面的步骤不变，最后一步的哈密顿量最大化变为
实验
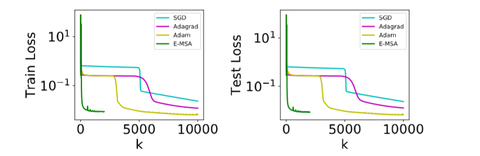
终于到实验了，论文中做了一些关于MSA和梯度下降方法的对比实验，首先是比较简单的函数逼近实验，用神经网络去逼近函数 ，而损失函数为平方损失，具体细节可看原论文，不过有一点需要注意，就是作者在实验中采用了10次迭代的limited memory BFGS方法(L-BFGS)来实现MSA算法中的哈密顿量最大化，L-BFGS是一种拟牛顿法，用来寻找最优解，感兴趣的话可以参看有关文章。
实验结果如下：
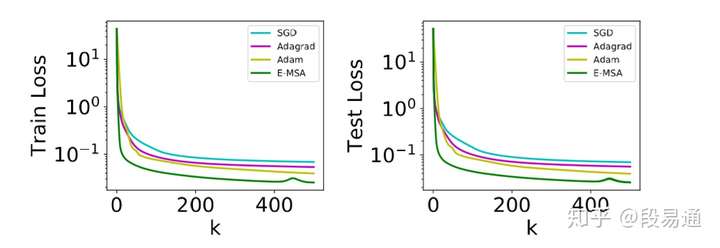
可以看出，E-MSA的每次迭代的收敛速度确实比梯度下降方法快一些。另外，梯度下降法的一大问题就是如果参数初始化得不好，那么就有可能会遇到一些局部平坦的区域，导致收敛速度变慢，而MSA方法则不会受到这个问题的影响，如下图所示
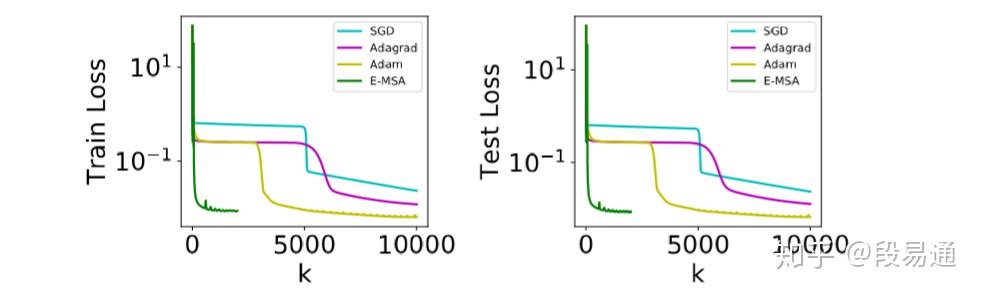
除了简单的函数近似，作者还做了MNIST数据集上手写数字识别的对比实验，如下图所示
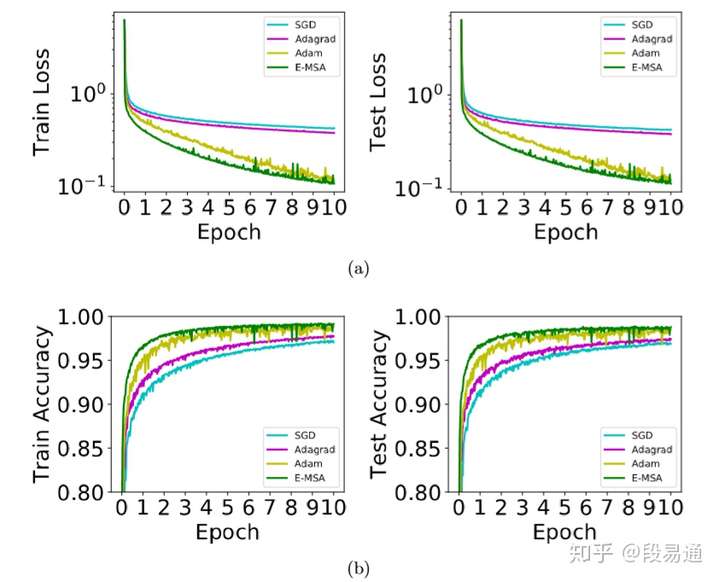
然而，论文中也提到了MSA的一个很大的不足之处，那就是每轮迭代的时间会比梯度下降慢得多，这是可以理解的，毕竟MSA的每轮迭代都需要去找到一个最大值，而梯度下降只需要计算一次梯度就行了。这就导致了虽然MSA每次迭代收敛地更快，但是从时间上来看却反而更慢了，如下所示。
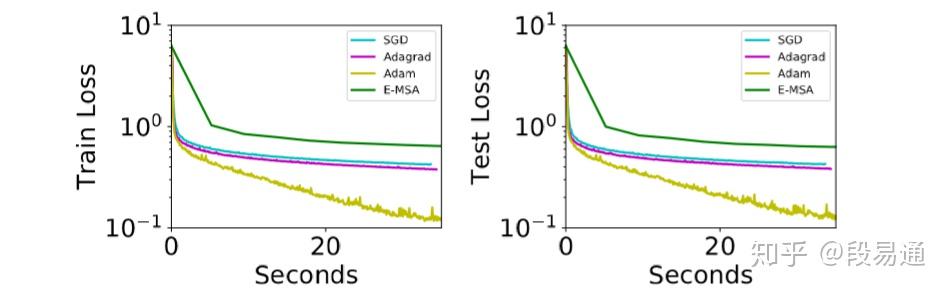MNIST数字识别对比
总结
先总结一下MSA的优点：
- 收敛得更快，而且并不需要精心设置初始化的训练参数。
- 对于参数空间的要求很低，甚至可以是离散的，这就使得我们可以设计一些具有离散参数值的神经网络层。
- 迭代中的最大化是对于每一层分别进行的，因此参数空间大大减小。
- 神经网络层都是相似的，一般就那么几种，因此它们的哈密顿量的形式也有限，这样我们就可以专门针对这些哈密顿量设计一些特殊的优化算法。
- 在实际迭代中，我们并不需要对哈密顿量实现完全最大化，只需要比上一步有所增加就行，因此可以引入一些快速的启发式算法。
总的来说，E-MSA能否最终替代梯度下降法，关键在于能否以合理的计算代价实现高效的哈密顿最大化。
总结一下全文，这篇论文从动力学系统的角度出发，将残差网络看作是其时间离散化的情况，从而将监督学习问题看作是对一个最优控制问题的求解，通过参考控制领域内的PMP和MSA这些已有的方法，作者提出了针对深度学习的离散化Extended MSA，并且证明了现在的梯度下降法只不过是Basic MSA的一个变种，通过实验表明了E-MSA确实解决了梯度下降法存在的一些问题，不过它本身也同样有待于进一步的改进。
参考资料
[1] Maximum Principle Based Algorithms for Deep Learning
[2] 庞特里亚金最大化原理_百度百科
[3] https://www.zhihu.com/question/315809187/answer/623687046
加速对抗训练——YOPO算法浅析
随着深度学习的不断发展，基于深度神经网络（DNN）的模型在很多数据集上的表现都已经超越了人类的水平，然而对抗攻击(adversarial attack)的出现却让我们开始怀疑DNN是否真正学习到了有用的信息。对抗攻击大致可以理解为，给定一张猫的图片，训练好的DNN可以准确地对图片进行分类，然而如果在原始图片上加上一些特定的噪音，虽然在人的肉眼看来这张图片几乎没有什么改变，仍然可以清晰地认出这是一只猫，但是DNN却有可能得到一个完全不同的分类结果。换句话说就是，输入样本的微小改变就可能会导致模型的准确度大幅度下降。
为了解决这个问题，模型在训练时就需要采用对抗训练(adversarial training)的方式，然而传统的对抗训练需要花费的时间较长，而本文介绍的这篇论文就提出了一种通过极大值原理(Pontryagin's Maximum Principle, PMP)来加速对抗训练的YOPO(You Only Propagate Once)算法。下面就来具体介绍YOPO相比于传统方法速度快在了哪里。
首先说明一下，这篇论文和我上一次介绍的论文很相关，所以部分内容就不再赘述了，为了更容易理解本篇文章，建议没看过我上一篇文章的读者可以先看那篇，下面是链接。
段易通：替代梯度下降——基于极大值原理的深度学习训练算法zhuanlan.zhihu.com
Differential Game
在上篇文章中已经提到了，对于一个残差神经网络，其实可以用动力学系统的角度来看待它，而网络的训练过程则可以看作是对动力学系统实现最优化控制。而本篇论文则是将对抗训练看作一个differential game，differential game可以理解为：有两个参与者，他们控制同一个动力学系统，一个人的目标是最大化系统最终的payoff，而另一个人则想要最小化payoff。
放到对抗训练中来看，其中一个参与者就是神经网络，它通过改变网络权重来最小化最终的目标函数，而另外一个参与者就是adversary，它要做的就是对抗攻击，通过修改输入的方式来最大化目标函数。那么对抗训练的优化问题就可以写成如下的形式：
公式中的符号设定与上一篇文章基本一致，这里只提一些关键的地方：
- 函数
就是目标函数，
就是神经网络中的参数，而
则是对抗攻击中对于输入的扰动，它不能任意取值，需要被约束在一个
-ball 里面。
- N代表样本数，T代表神经网络层数，网络中的层就由
函数来表示。需要注意这里与上一篇文章有所不同，上一篇文章中网络层之间用的是残差网络的传递关系：
，这样的话就需要通过常微分方程的数值解法来求解，而现在这里做了一些改动，作者直接采用了通用的
方式。
- 原始输入就是
，对于第0层网络
（实际上是网络的第一层，不过为了与符号对应就叫做第0层吧），我们需要在原始输入
，然后再经过一层层
的作用，最终得到
。之后再通过函数
计算loss，并加上关于权重
的正则项
，得到最终的目标函数。
Projected Gradient Descent
明确了优化问题以后，我们就可以设计相应的算法来寻找最优解了，首先把上面的优化问题简写一下，变成：
其中 还是代表网络的第0层，而
，代表网络中除去第0层以外的其它层的共同作用；B是一个batch的样本数量。简便起见，这里忽略了正则项
，下文中将会说明这样做是可以的。
对于这样的一个优化问题，一种非常简单的解决方法就是：先对对抗攻击参数 进行梯度上升，然后再对网络权重参数
进行梯度下降，这样不断地迭代直到收敛，最终得到的网络就能很好地抵御对抗攻击了。这种算法被叫做Projected Gradient Descent(PGD)，它的具体步骤如下：
PGD-r算法
它的思路很简单，就是先对 执行r次梯度上升，然后再对
做一次梯度下降，完成一次权重更新。这样一来，每更新一次
，就需要先对
做r次正向和反向传播，这就导致了PGD-r的训练速度非常慢。
YOPO算法（梯度下降版本）
为了解决速度慢的问题，论文作者提出了一种能够减少计算正反向传播次数的新方法，具体来说，首先令
在对 更新的循环中，我们把p固定，认为它不会随着
的改变而改变，这样的话梯度的计算公式就从
变为：
我们只需要计算 对于网络第0层
的梯度，这样就减少了正反向传播的层数，从而加快速度。算法的完整流程如下：
YOPO-m-n算法
简单分析一下这个算法，首先给定一个初始的 ，计算出对应的p，然后在固定p的情况下做n次梯度下降得到
，接着完成更新：
，并重新计算p，这样进行m步，就得到了 集合
，最后用这m个
完成对于参数
的动量SGD。
可以看出，虽然YOPO-m-n关于参数 的迭代更新中实际上只计算了m次p，也就是只完成了m次完整的正反向传播，但是却实现了m*n次梯度下降。而PGD-r算法完成r次完整的正反向传播却只能实现r次梯度下降。这样看来，YOPO-m-n算法的效率明显更高，而实验也表明，只要使得m*n略大于r，YOPO-m-n的效果就能够与PGD-r相媲美。
将极大值原理用于对抗训练
说到这里其实才进入了这篇论文的核心内容，前面的那个YOPO算法在本质上还是一个基于梯度下的方法，而只要是梯度下降，就必须要一层层地计算出反向传播的loss，不过YOPO在迭代中通过“冻结”p的方式减少了计算传播的次数，这种“冻结”的方法究竟有没有道理？下面我们将证明这种“冻结”p的方式是有理论支持的，它其实是极大值原理（PMP）版本YOPO算法的一种特殊形式。
通过上一篇文章可以知道，运用极大值原理（PMP）的参数训练方法可以替代梯度下降，而它最大的特点就是网络参数在优化时，层与层之间是解耦的，也就是说PMP方法在优化 时，只需要对
所在的第0层进行优化，而不需要去计算其它层的梯度传播，这样就大大提高了效率。下面将具体介绍PMP如何用于对抗训练。
对于每一层t，定义哈密顿量的形式为：
那么就可以得到如下PMP定理：
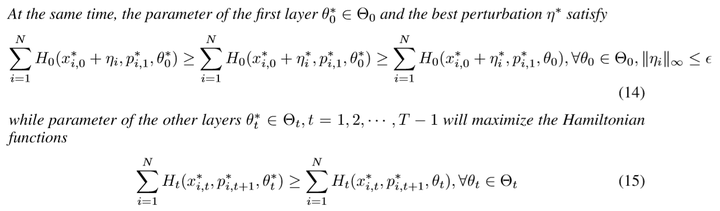
关于这个定理的证明，可以看本文最后的附录。
这个定理看起来很复杂，其实还是上一篇文章中PMP的那些东西，简单来说，对于优化问题：
如果该问题存在最优解，那么相应的最优参数 和
以及
和协态
就一定满足下列条件：
通过分析这几个PMP条件可以看出，参数 的优化其实只和第三个条件有关，而第三个条件需要计算的只是关于网络第0层的哈密顿量，这样就使得参数
的优化与其余层解耦，在优化时也就不用去考虑正反向传播了（其实上一篇文章中已经提到了，正反向传播是分别通过x和p来完成的，分别对应着上面的第1、2个条件，与条件3无关）。
YOPO算法（PMP版本）
PMP的这些条件虽然只是最优解的必要条件，但是它们已经很强了，能够满足这些条件的解一般都是最优解。因此如果我们能够设计一个能够去逼近PMP解的算法，那么就能够用它来取代原先梯度下降的算法。PMP版本的YOPO算法如下：
首先，这个算法通过不断迭代的方式来逼近PMP条件的解。算法流程和上一篇文章中的MSA算法基本一致，只是在优化哈密顿量的步骤有所不同，这里简单说一下前面的流程：给定初始条件后，第一步是通过正向传播计算出每一网络层的 （图中红框部分），第二步通过反向传播计算出
（图中蓝框部分） ，这两步的具体分析可看上一篇文章的MSA算法。
接下来重点讨论优化步骤，按照YOPO算法的流程，首先我们应该优化参数 使得目标函数最大，而PMP条件告诉我们，
的最优参数
其实只需要满足条件：
那么我们原先通过对目标函数作梯度上升来更新 的方式，就可以变为对网络第0层的哈密顿量
求
（也就算法中划绿线的部分）。按照YOPO算法，这样进行m次迭代之后，接着就需要对参数
进行优化来使得目标函数达到最小，而在PMP中，这样的优化可以变成分层解耦的形式，即最优参数
只需要对每一层的哈密顿量满足：
这样，原先用梯度下降来更新 的方式就变为了算法中的紫框部分，注意在对
进行最大化时，算法中采用了类似于动量梯度下降的方法（作者说这样可以防止过拟合），不是只考虑最新的
，而是考虑了整个历史集合
，对这m个
的H的平均值进行
，这样就完成了一次迭代。在多次迭代直到算法收敛之后，我们就得到了PMP的解，从而完成了对于参数的优化。
两种YOPO之间的关系
在上面的讨论中，我们分别用梯度下降和PMP得到了两种版本的YOPO，而下面我们将证明梯度下降版本只不过是PMP版本的一种特殊情况而已。
看到这里，你可能会想起上一篇文章中那个“软化”的最大化操作，没错，下面的证明与之前那个“软化”的证明基本是相同的，不过这里比较重要，所以我再从头推导一遍：
回忆一下，目标函数 的形式为：
而哈密顿量
当算法已经完成正向和反向传播（即红框和蓝框两部分）时，对于 ，从
递推可以得到：
注意，这里为了方便，令样本数N=1，这并不影响最终的结论。
那么参数 关于
的导数就可以写做：
可以发现，如果我们把PMP版本算法中的 哈密顿量操作（即紫框部分），看成是只沿着梯度上升的方向更新一步，即
那么其实它就是老版本YOPO中的梯度下降：
而对于算法中 的操作，如果我们把它看成是沿着梯度下降的方向更新n步，则有
在这n步更新过程中，反向传播得到的 是固定不变的，每步只计算
关于
的梯度，可以看出，其实它就是老版本YOPO中的n步梯度上升：
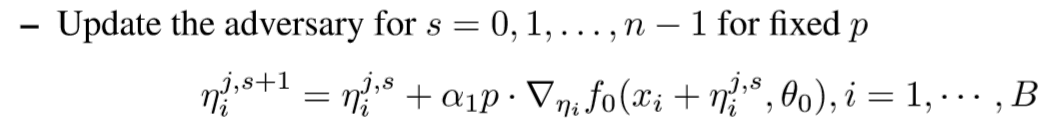
这也就解释了为什么我们在老版本YOPO算法中可以“冻结”p，这其实就是PMP版本在一些限制下的结果。这样我们就明白了两种YOPO算法之间的关系——梯度下降版本只是PMP版本的一个特例。
说到这里，我们就能够看懂下面这张图了
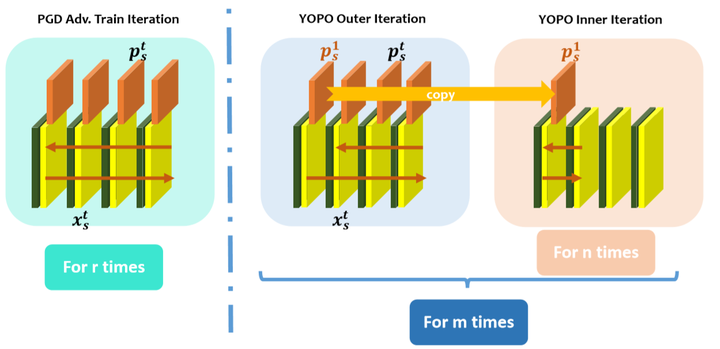PGD与YOPO算法流程对比
其中橄榄绿和黄色的块代表网络中间层的 ，橘红色的块代表每一层对于loss的梯度，也就是
。
左边是传统的PGD-r算法，可以看出，每要更新一次第0层的 ，就需要完成一次完整的正向传播和反向传播，而PGD-r算法每迭代一次
都需要进行r次这样的更新。
右边是YOPO-m-n算法，同样是更新第0层的参数 ，首先也同样需要进行
的正向传播，然后进行
的反向传播，不同的是在得到
之后，将它拷贝一份，利用
和函数
来计算
的梯度并执行n次梯度下降，然后再进行下一次的正反向传播。这样一来，YOPO-m-n每进行一次完整的正反向传播，都可以完成
的n次更新。
实验
对于实验，这里只简单介绍一下，感兴趣的读者可以看论文原文。
作者首先对PGD和YOPO算法在MNIST和CIFAR10两个数据集上进行了对比，结果如下：
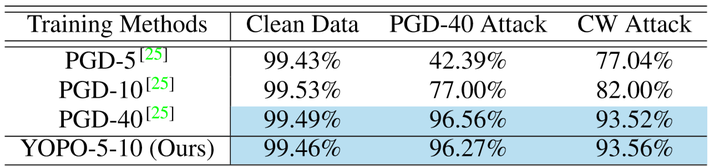MNIST结果
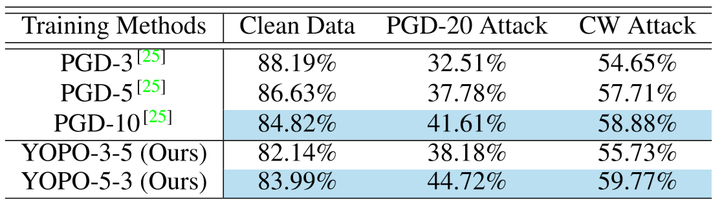CIFAR-10结果
而算法在训练过程中的错误率-时间曲线如下：
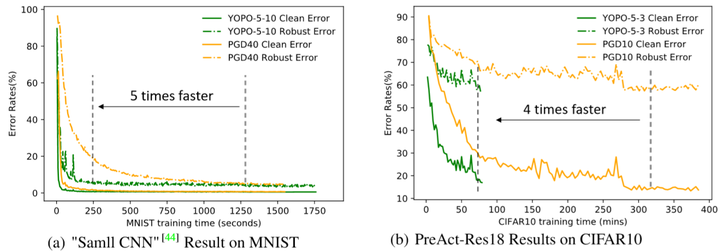
可以看出当准确率差不多时，YOPO的收敛速度比PGD快很多。
另外，作者还将YOPO做了一点改进，把原先的目标函数 替换掉，采用了在对抗训练中表现最好的TRADES算法的目标函数（这一部分可看论文中的补充材料），变成TRADES-YOPO算法，结果如下：
附录：PMP证明
最后来具体证明一下为什么PMP对于对抗训练是成立的，也就是证明之前那四个条件是优化问题最优解的必要条件。
首先我们先不考虑对抗攻击，也就是在输入数据中先不加 ，那么优化问题就变成了：
我们将证明，对于该问题的最优解 ，它将能够满足下列三个条件：
其中
下面开始证明，首先我们可以认为优化问题中的正则项，也就是 ，可以这么做的原因是可以在x中在额外加一个维度的分量w，使得
我们可以通过修改 为
，再相应地修改函数
来实现，这样
就不需要显式地出现在公式中了。
现在给这样的两个集合：
对于 ，可以这样去理解，由于
可以看作是初始状态
在参数
的控制下，在时间t到达的状态，那么
就是系统在t时所有可能到达状态的集合。而对于集合
，由于
已经是控制问题的最优结果了，那么
就是所有比最优结果还要好的状态集合（这是有可能的，因为最优的
是在满足约束条件下得出的）。可以看出，对于
和
，这两个集合之间是没有交集的。
现在，我们对这两个集合做一些改动，令：
简单分析一下这个关于 的递推公式，我们可以看出，当参数
时，有
，这个结论在下面的证明中会用到。
则得到两个新的集合：
之所以这么做，是因为这样就使得两个新的集合是凸集，而构造凸集的动机是为了下面这个重要的线性化引理：
引理：如果和
两者不相交，那么
和
就可以被一个超平面分离，这个超平面是：
对于集合 ，满足
而由于
经过推导可以发现
再考虑到集合 的性质，则有
现在进入整个证明最核心的部分，我们通过反证法来证明PMP的哈密顿量最大化条件：
假设存在参数 使得
其中 ，这就意味着
现在构建这么一个模型，对于网络的前t层： ，有
，而对于第t层，参数
，那么根据
递推公式的结论，就有
那么根据 的要求，就有
，但是这却违反了上面所有的t都要满足
的要求，出现矛盾，因此
不存在，即优化问题最优解
一定是哈密顿量H的最大解，PMP条件得证。
现在我们来证明加上对抗攻击之后的PMP定理，稍微修改一下函数： ，
，则对抗攻击的优化问题变为：
现在，所有的层的参数 都是固定的，需要优化的是
，那么同样套用上面已经证明的定理，对于最优的
，一定满足条件:
其中
则有
其中
带入不等式则有
也就是
这样就完成了整个定理证明。
参考资料
[1] You Only Propagate Once: Accelerating Adversarial Training via Maximal Principle
[2] An Optimal Control Approach to Deep Learning and Applications to Discrete-Weight Neural Networks