非线性泛函分析导论(二):变分问题的拓扑结构
【上节回顾】
我们已经了解了 Sobolev 嵌入定理、Rellich 紧嵌入定理以及如何给 Sobolev 空间上的非线性泛函做导数演算——也就是变分。我们也了解到,与有限维的函数极值问题相比,无限维空间的泛函取到极值需要更加严格的条件——集合的弱紧性 + 泛函的弱连续性。我们还简要介绍了约束泛函极值的 Lagrange 乘子定理,并做了一个简单的应用:特征值问题。最后,我们还介绍了测度论中有关 Caratheodory 映射的重要结果,这一些结果与我们熟悉的 Holder 不等式结合起来可以证明许多泛函的可微性。先给出上篇文章的传送门:
必须说明的是:对 Lagrange 乘子定理的理解我们没有过多阐述,这是因为我们还需要 Banach 空间的隐函数定理(非常重要,留待以后介绍)。待我们面对 Nehari 流形的时候,我们会再次回顾乘子定理。
为了更加深入地处理非线性问题,本篇文章不得不开始引入一些拓扑学工具。说实话,泛函分析仅仅停留在本科的线性算子理论是没有出路的,但是只要你开始处理非线性问题,那么拓扑工具是怎么也绕不过去的坎儿。不过,我们只把对拓扑的介绍控制在必要的最低的限度内,事实上,这些内容仅仅是代数 / 微分拓扑的皮毛知识罢了。
【Ekeland 变分原理】
上节我们已经熟知了泛函取到极值的充分必要条件。但是我们需要验证弱紧性、弱下半连续性。下面给出的定理指出泛函近似极小点存在的条件。


当 Ekeland 变分原理与 P.S. 条件结合起来时,会给出一个非常重要的推论。

需要指出的是,条件 14.18 中 Frechet 导数的范数趋于零的意思是:Frechet 导数作为线性算子的范数趋于零!


【拓扑形变、映射度与流形的环绕】
先简要介绍形变引理。需要指出的是,在本篇文章中,我们暂时还无法给出形变引理的完整表述。但为了节约下篇文章的篇幅,我还是在这里解释一下形变引理的几何直观。

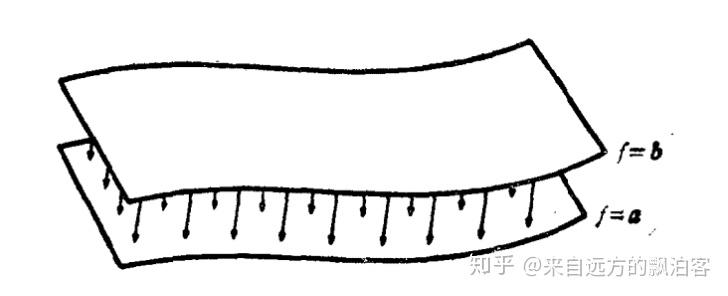
也就是说,如果区间【a,b】内没有函数的临界值,那么函数的水平集是同胚的。最简单的例子可以用环面的高度函数来理解。
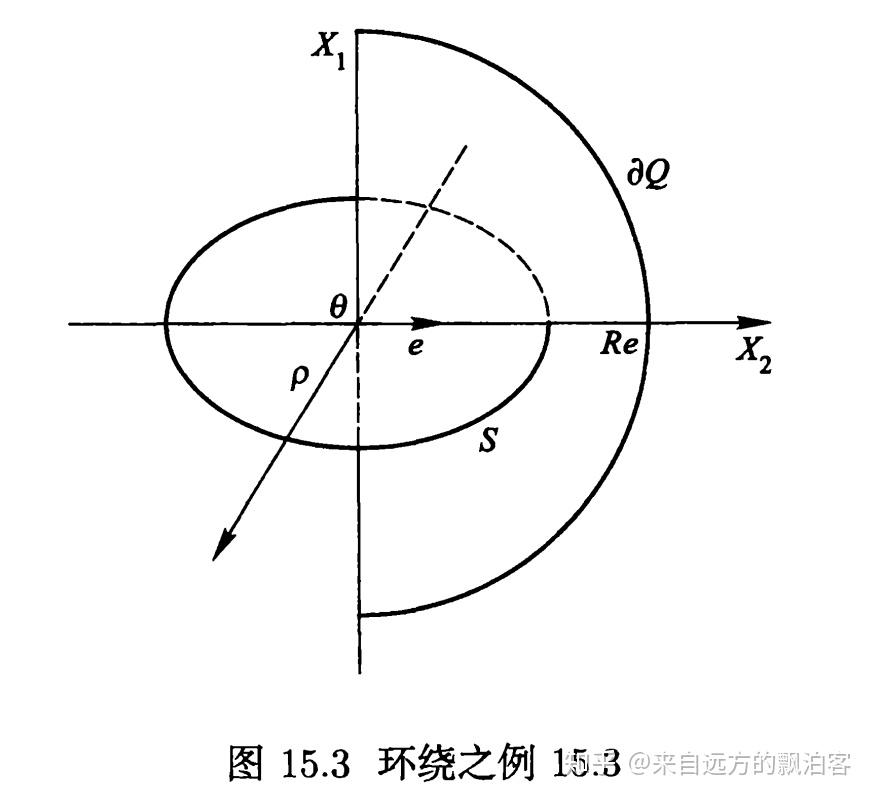
考虑环面 M 切于平面Π,如下图:
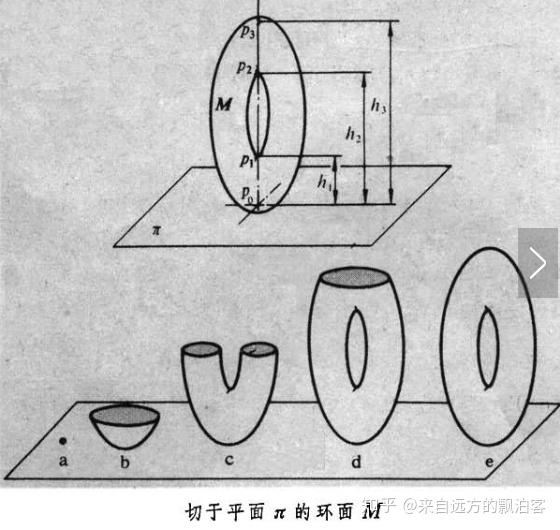
设函数
是 M 关于平面Π的高度。这个例子表明:若在实数α 、b (α <b ) 之间没有f 的临界值,则函数的水平集
与
是同胚的, 但当函数值 c 扫过ƒ 的一个临界值时, 函数的水平集
的拓扑结构将发生变化。因此,我们可以根据函数水平集的拓扑性质是否发生变化来判定函数临界点的存在性!
放到无限维空间也是一样:我们可以根据泛函水平集的拓扑性质是否发生变化来判定泛函临界点的存在性。这就是大范围变分法的基本出发点。
我们学过偏微分方程,应该都知道一个偏微分方程解的存在性就可以转化为一个泛函的临界点的存在性。 我们通过研究 Sobolev 空间上一个泛函临界点的存在性,可以推出对应 PDE 弱解的存在性,然后通过 PDE 的正则性理论来提升弱解的光滑性。这就是现代偏微分方程研究的套路之一。
接下来我们介绍映射度。这个工具最早是由拓扑学家 Brouwer 提出的,现在在泛函分析中广为流传(几乎是任何一本非线性泛函分析必讲的内容)。先给出定义及其性质:


以上五条是映射度最最基本最最常用的性质。概括地说,如果我们想要证明命题:
这类命题显然是极度普遍的。那么我们只需要证明:
(这就是 Kronecker 存在性)映射度的威力可见一斑!
恒同映射的映射度为 1,这样,如果我们能把 f 与恒同映射同伦起来(且验证满足性质 2:同伦不变性),就可以做到这一点。
映射度相应的无限维版本称为 Lery-Schaulder 度。然而对于我们目前来说,Brouwer 度已经足够。
现在我们给出环绕的概念:

利用 Brouwer 映射度,我们可以证明两个流形是环绕的。
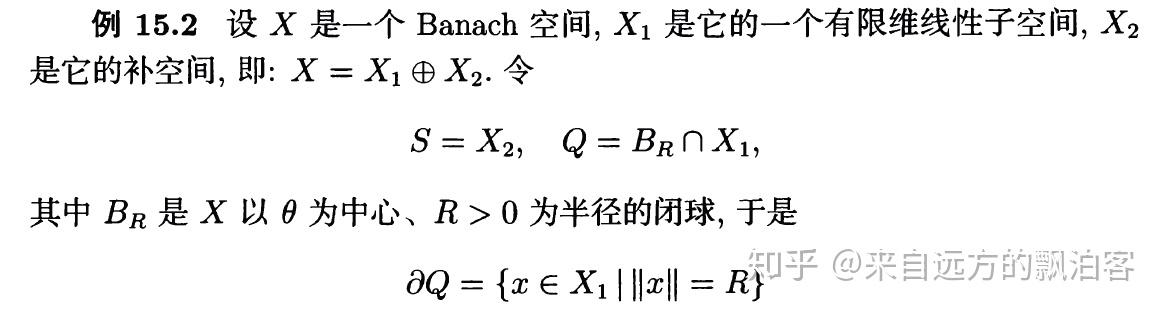
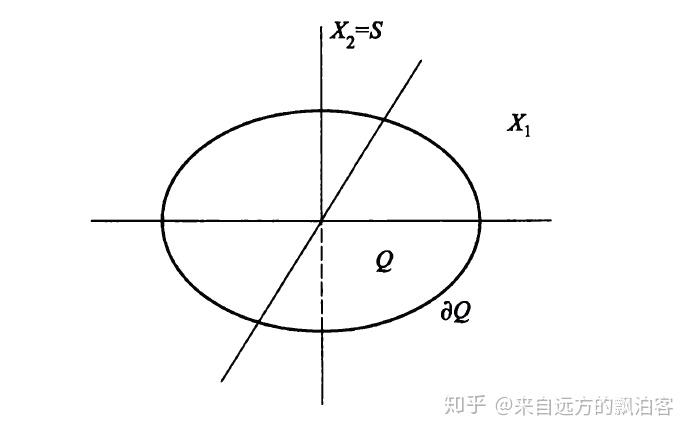

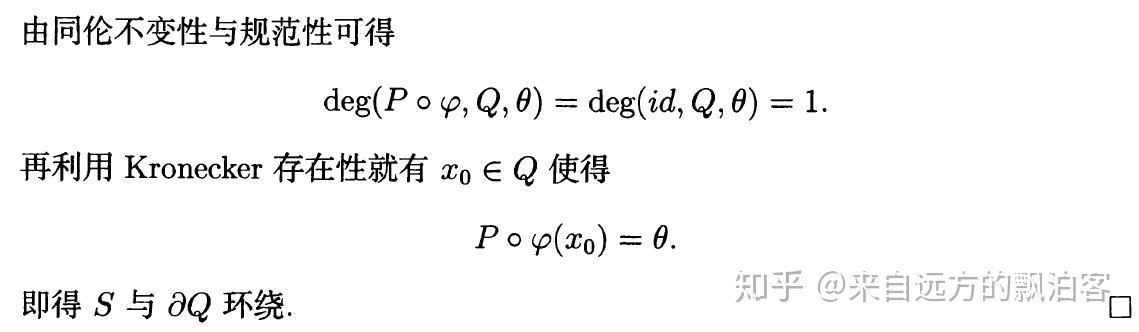
我们再来看一个稍微难一点的练习:




本文的最后,我们给出大范围变分法的第一个定理:
环绕定理
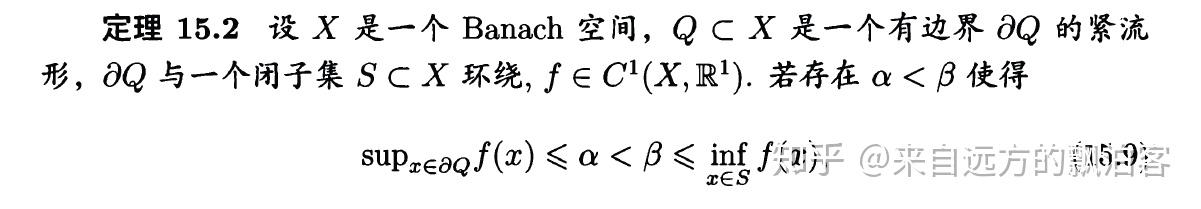
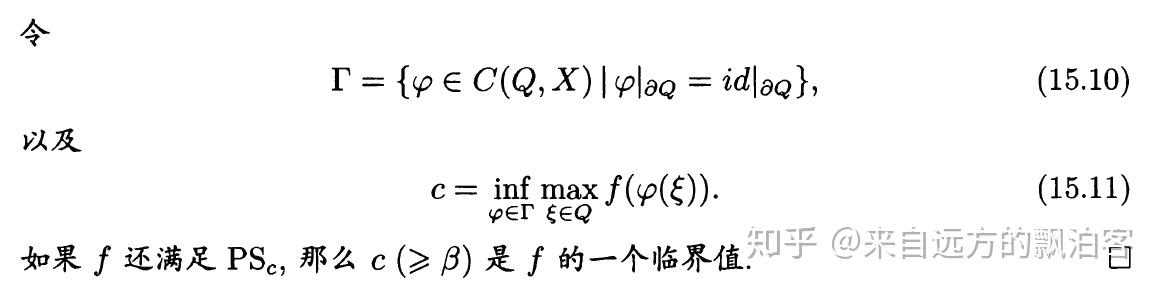
当然,这个定理太过一般化(有点像哲学命题),不便于应用。事实上,只要稍加特殊化,我们就可以得到著名的山路定理(Mountain Pass theorem by A.Ambrosetti and P.H.Rabinowitz)。事实上,通过构造不同的环绕结构,利用环绕定理,我们可以造出形形色色的临界点定理。


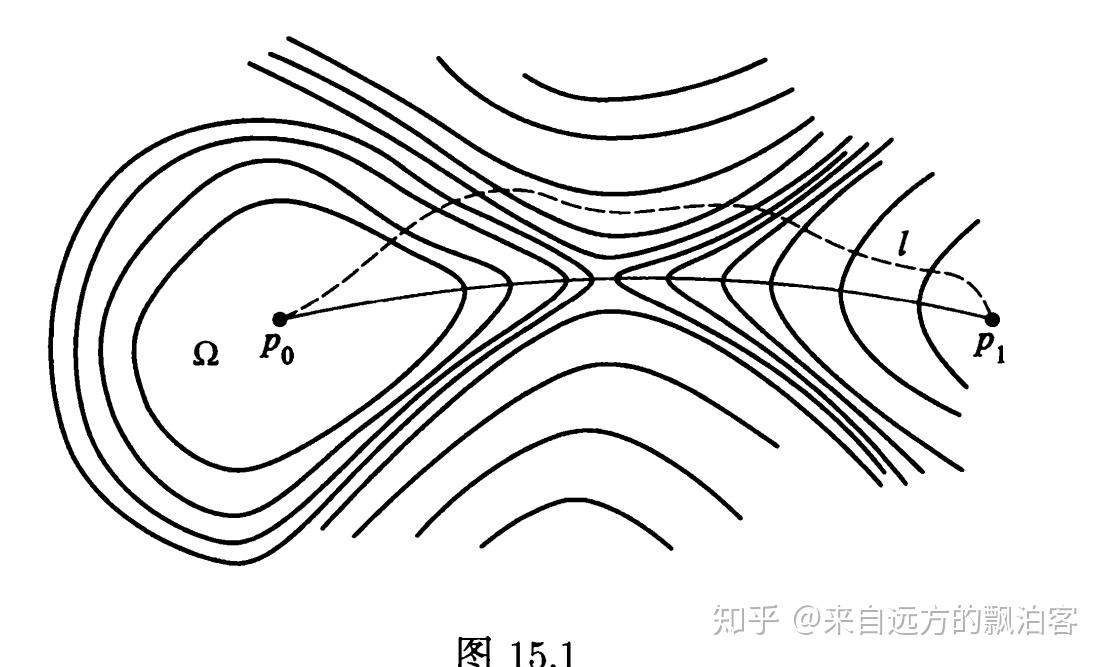

事实上,我们只要取:
,显然
与 S 环绕。带入到环绕定理即可证明山路定理。
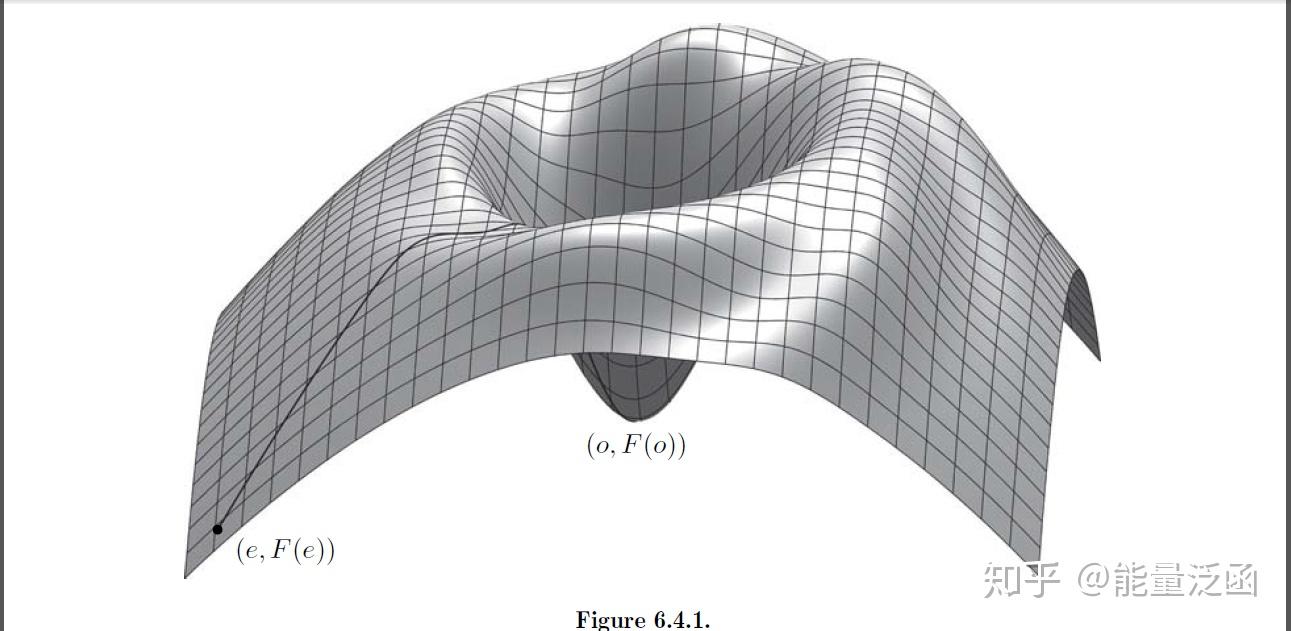
粗略地讲,从山谷谷底去往山外另一处低洼地带,你必须先爬坡,再下山,这其中会经过一个临界点。
山路定理是非线性分析、非线性 PDE 理论中非常重要的一个定理。它是环绕定理的特例,也可以用 Ekeland 变分原理证明。不过更多的时候,我们还是借助于形变引理、通过反证法来证明它。
to be continued
不明觉厉,还在学数分的我瑟瑟发抖...
慢慢来不急
Morse 理论?
是的,不过还没到那个深度。只是非线性泛函导论性质的文章。
最近看 Evans 的 PDE 的时候看到这部分。讲得很好,点个赞!
谢谢
请问截图都出自哪本书?谢谢
专栏介绍里有
不止一本
全文完