要求
- 给定一个正数n,可将其分割成多个数字的和,求让这些数字乘积最大的分割方法(至少分成两个数)
示例
- n=2,返回1(2=1+1)
- n=10,返回36(10=3+3+4)
实现
- 回溯遍历(n^2,超时)
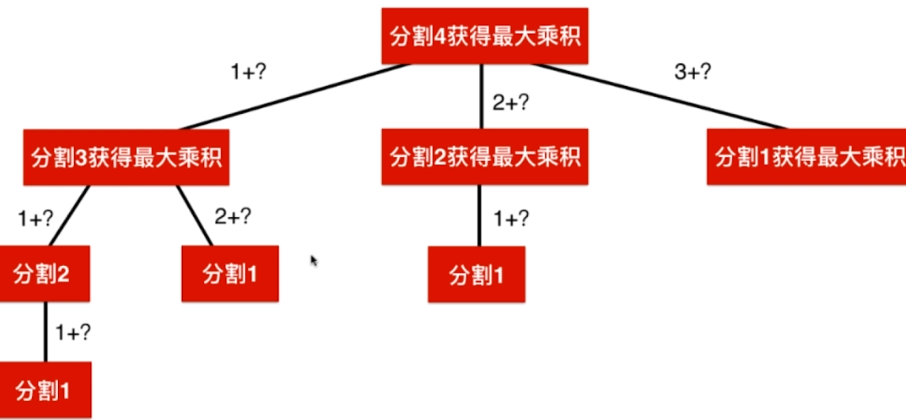

1 class Solution { 2 private: 3 int max3( int a , int b , int c ){ 4 return max( a , max(b,c) ); 5 } 6 7 // 将n进行分割(至少两部分)可获得的最大乘积 8 int breakInteger(int n){ 9 10 if( n == 1 ) 11 return 1; 12 13 int res = -1; 14 for( int i = 1 ; i <= n-1 ; i ++ ) 15 // i + (n-i) 16 res = max3( res, i * (n-i) , i * breakInteger(n-i) ); 17 18 return res; 19 } 20 21 public: 22 int integerBreak(int n) { 23 return breakInteger(n); 24 } 25 };
- 记忆化搜索
- 21:不要写成 res=max(res,i*breakInteger(n-i)),breakInteger(n-i) 将 n-i 至少分成两部分,不分割的话就是 i*(n-i)
- 自定义传入3个数求最大值的函数

1 class Solution { 2 private: 3 vector<int> memo; 4 5 int max3( int a , int b , int c ){ 6 return max( a , max(b,c) ); 7 } 8 9 // 将n进行分割(至少两部分)可获得的最大乘积 10 int breakInteger(int n){ 11 12 if( n == 1 ) 13 return 1; 14 15 if( memo[n] != -1) 16 return memo[n]; 17 18 int res = -1; 19 for( int i = 1 ; i <= n-1 ; i ++ ) 20 // i + (n-i) 21 res = max3( res, i * (n-i) , i * breakInteger(n-i) ); 22 memo[n] = res; 23 return res; 24 } 25 26 public: 27 int integerBreak(int n) { 28 memo = vector<int>(n+1,-1); 29 return breakInteger(n); 30 } 31 };
- 动态规划
- 重叠子问题:有相同的子问题,可采用记忆化搜索进行优化
- 最优子结构:通过求子问题的最优解,可以获得原问题的最优解
- 如:想获得分割n的最大乘积,需要知道分割n-1,n-2...,1等的最大乘积
- 满足重叠子问题 + 最优子结构的递归问题,可以用记忆化搜索/动态规划求解

1 class Solution { 2 private: 3 int max3( int a , int b , int c ){ 4 return max( a , max(b,c) ); 5 } 6 7 public: 8 int integerBreak(int n) { 9 assert( n >= 2 ); 10 11 // memo[i]表示至少将数字i分割(至少两部分)后得到的最大乘积 12 vector<int> memo(n+1,-1); 13 14 memo[1] = 1; 15 for( int i = 2 ; i <= n ; i ++ ) 16 // 求解memo[j] 17 for( int j = 1 ; j <= i-1 ; j ++ ) 18 // j + (i-j) 19 memo[i] = max3(j*(i-j) , j*memo[i-j] , memo[i] ); 20 21 return memo[n]; 22 } 23 };
相关
- 279 Perfect Squares
- 91 Decode Ways
- 62 Unique Paths
- 63 Unique Paths II
