初始化

分别使用0、随机数和抑梯度异常初始化参数,比较发现抑梯度异常初始化参数可以得到更高的准确度。
原始数据:
import numpy as np import matplotlib.pyplot as plt import sklearn import sklearn.datasets from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec from math import sqrt # %matplotlib inline plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots plt.rcParams['image.interpolation'] = 'nearest' plt.rcParams['image.cmap'] = 'gray' # load image dataset: blue/red dots in circles train_X, train_Y, test_X, test_Y = load_dataset()
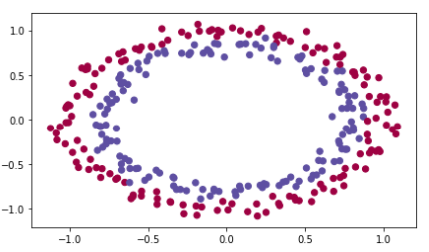
使用抑梯度异常初始化代码如下:

1 #three layers 2 def model(X, Y, learning_rate=0.01, num_iterations=15000, print_cost=True, initialization="he"): 3 """ 4 Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID. 5 6 Arguments: 7 X -- input data, of shape (2, number of examples) 8 Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples) 9 learning_rate -- learning rate for gradient descent 10 num_iterations -- number of iterations to run gradient descent 11 print_cost -- if True, print the cost every 1000 iterations 12 initialization -- flag to choose which initialization to use ("zeros","random" or "he") 13 14 Returns: 15 parameters -- parameters learnt by the model 16 """ 17 18 grads = {} 19 costs = [] # to keep track of the loss 20 m = X.shape[1] # number of examples 21 layers_dims = [X.shape[0], 10, 5, 1] 22 23 # Initialize parameters dictionary. 24 parameters = initialize_parameters_he(layers_dims) 25 26 # Loop (gradient descent) 27 for i in range(0, num_iterations): 28 29 # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID. 30 a3, cache = forward_propagation(X, parameters) 31 32 # Loss 33 cost = compute_loss(a3, Y) 34 35 # Backward propagation. 36 grads = backward_propagation(X, Y, cache) 37 38 # Update parameters. 39 parameters = update_parameters(parameters, grads, learning_rate) 40 41 # Print the loss every 1000 iterations 42 if print_cost and i % 1000 == 0: 43 print("Cost after iteration {}: {}".format(i, cost)) 44 costs.append(cost) 45 46 # plot the loss 47 plt.plot(costs) 48 plt.ylabel('cost') 49 plt.xlabel('iterations (per hundreds)') 50 plt.title("Learning rate =" + str(learning_rate)) 51 plt.show() 52 53 return parameters 54 55 56 # GRADED FUNCTION: initialize_parameters_he 57 def initialize_parameters_he(layers_dims): 58 """ 59 Arguments: 60 layer_dims -- python array (list) containing the size of each layer. 61 62 Returns: 63 parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": 64 W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) 65 b1 -- bias vector of shape (layers_dims[1], 1) 66 ... 67 WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) 68 bL -- bias vector of shape (layers_dims[L], 1) 69 """ 70 71 np.random.seed(3) 72 parameters = {} 73 L = len(layers_dims) - 1 # integer representing the number of layers 74 75 for l in range(1, L + 1): 76 ### START CODE HERE ### (≈ 2 lines of code) 77 parameters['W'+str(l)]=np.random.randn(layers_dims[l], layers_dims[l-1])*sqrt(2./layers_dims[l-1]) 78 parameters['b'+str(l)]=np.zeros((layers_dims[l], 1)) 79 ### END CODE HERE ### 80 return parameters 81 82 parameters = initialize_parameters_he([2, 4, 1]) 83 print("W1 = " + str(parameters["W1"])) 84 print("b1 = " + str(parameters["b1"])) 85 print("W2 = " + str(parameters["W2"])) 86 print("b2 = " + str(parameters["b2"])) 87 88 89 parameters = model(train_X, train_Y, initialization = "he") 90 print("On the train set:") 91 predictions_train = predict(train_X, train_Y, parameters) 92 print("On the test set:") 93 predictions_test = predict(test_X, test_Y, parameters) 94 95 96 plt.title("Model with He initialization") 97 axes = plt.gca() 98 axes.set_xlim([-1.5, 1.5]) 99 axes.set_ylim([-1.5, 1.5]) 100 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
预测准确度0.96

L2正则化

原始数据:
1 from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec 2 from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters 3 import scipy.io 4 from testCases_v3 import * 5 6 train_X, train_Y, test_X, test_Y = load_2D_dataset()
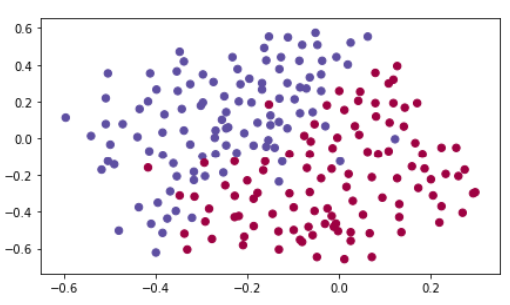
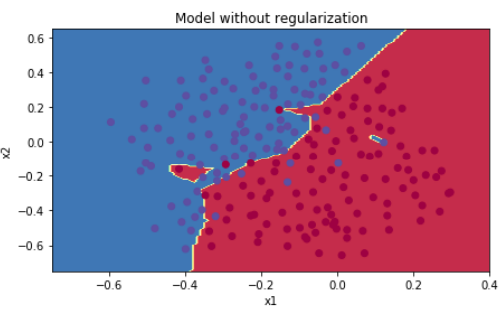
如果不使用正则化:

1 def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1): 2 """ 3 Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID. 4 5 Arguments: 6 X -- input data, of shape (input size, number of examples) 7 Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples) 8 learning_rate -- learning rate of the optimization 9 num_iterations -- number of iterations of the optimization loop 10 print_cost -- If True, print the cost every 10000 iterations 11 lambd -- regularization hyperparameter, scalar 12 keep_prob - probability of keeping a neuron active during drop-out, scalar. 13 14 Returns: 15 parameters -- parameters learned by the model. They can then be used to predict. 16 """ 17 18 grads = {} 19 costs = [] # to keep track of the cost 20 m = X.shape[1] # number of examples 21 layers_dims = [X.shape[0], 20, 3, 1] 22 23 # Initialize parameters dictionary. 24 parameters = initialize_parameters(layers_dims) 25 26 # Loop (gradient descent) 27 for i in range(0, num_iterations): 28 29 # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID. 30 if keep_prob == 1: 31 a3, cache = forward_propagation(X, parameters) 32 elif keep_prob < 1: 33 a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob) 34 35 # Cost function 36 if lambd == 0: 37 cost = compute_cost(a3, Y) 38 else: 39 cost = compute_cost_with_regularization(a3, Y, parameters, lambd) 40 41 # Backward propagation. 42 assert(lambd == 0 or keep_prob == 1) # it is possible to use both L2 regularization and dropout, 43 # but this assignment will only explore one at a time 44 if lambd == 0 and keep_prob == 1: 45 grads = backward_propagation(X, Y, cache) 46 elif lambd != 0: 47 grads = backward_propagation_with_regularization(X, Y, cache, lambd) 48 elif keep_prob < 1: 49 grads = backward_propagation_with_dropout(X, Y, cache, keep_prob) 50 51 # Update parameters. 52 parameters = update_parameters(parameters, grads, learning_rate) 53 54 # Print the loss every 10000 iterations 55 if print_cost and i % 10000 == 0: 56 print("Cost after iteration {}: {}".format(i, cost)) 57 if print_cost and i % 1000 == 0: 58 costs.append(cost) 59 60 # plot the cost 61 plt.plot(costs) 62 plt.ylabel('cost') 63 plt.xlabel('iterations (x1,000)') 64 plt.title("Learning rate =" + str(learning_rate)) 65 plt.show() 66 67 return parameters 68 69 70 parameters = model(train_X, train_Y) 71 print("On the training set:") 72 predictions_train = predict(train_X, train_Y, parameters) 73 print("On the test set:") 74 predictions_test = predict(test_X, test_Y, parameters) 75 76 77 plt.title("Model without regularization") 78 axes = plt.gca() 79 axes.set_xlim([-0.75, 0.40]) 80 axes.set_ylim([-0.75, 0.65]) 81 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
预测准确度0.915
使用了L2正则化:

1 # GRADED FUNCTION: compute_cost_with_regularization 2 def compute_cost_with_regularization(A3, Y, parameters, lambd): 3 """ 4 Implement the cost function with L2 regularization. See formula (2) above. 5 6 Arguments: 7 A3 -- post-activation, output of forward propagation, of shape (output size, number of examples) 8 Y -- "true" labels vector, of shape (output size, number of examples) 9 parameters -- python dictionary containing parameters of the model 10 11 Returns: 12 cost - value of the regularized loss function (formula (2)) 13 """ 14 m = Y.shape[1] 15 W1 = parameters["W1"] 16 W2 = parameters["W2"] 17 W3 = parameters["W3"] 18 19 cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost 20 21 ### START CODE HERE ### (approx. 1 line) 22 L2_regularization_cost=lambd/(2*m)*(np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) 23 ### END CODER HERE ### 24 25 cost = cross_entropy_cost + L2_regularization_cost 26 return cost 27 28 A3, Y_assess, parameters = compute_cost_with_regularization_test_case() 29 print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1))) 30 31 32 # GRADED FUNCTION: backward_propagation_with_regularization 33 def backward_propagation_with_regularization(X, Y, cache, lambd): 34 """ 35 Implements the backward propagation of our baseline model to which we added an L2 regularization. 36 37 Arguments: 38 X -- input dataset, of shape (input size, number of examples) 39 Y -- "true" labels vector, of shape (output size, number of examples) 40 cache -- cache output from forward_propagation() 41 lambd -- regularization hyperparameter, scalar 42 43 Returns: 44 gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables 45 """ 46 47 m = X.shape[1] 48 (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache 49 50 dZ3 = A3 - Y 51 52 ### START CODE HERE ### (approx. 1 line) 53 dW3=np.dot(dZ3,A2.T)/m+lambd*W3/m 54 ### END CODE HERE ### 55 db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True) 56 57 dA2 = np.dot(W3.T, dZ3) 58 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 59 ### START CODE HERE ### (approx. 1 line) 60 dW2=np.dot(dZ2,A1.T)/m+lambd*W2/m 61 ### END CODE HERE ### 62 db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True) 63 64 dA1 = np.dot(W2.T, dZ2) 65 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 66 ### START CODE HERE ### (approx. 1 line) 67 dW1=np.dot(dZ1,X.T)/m+lambd*W1/m 68 ### END CODE HERE ### 69 db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True) 70 71 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2, 72 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 73 "dZ1": dZ1, "dW1": dW1, "db1": db1} 74 return gradients 75 76 77 X_assess, Y_assess, cache = backward_propagation_with_regularization_test_case() 78 grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd=0.7) 79 print ("dW1 = " + str(grads["dW1"])) 80 print ("dW2 = " + str(grads["dW2"])) 81 print ("dW3 = " + str(grads["dW3"])) 82 83 84 parameters = model(train_X, train_Y, lambd=0.7) 85 print("On the train set:") 86 predictions_train = predict(train_X, train_Y, parameters) 87 print("On the test set:") 88 predictions_test = predict(test_X, test_Y, parameters) 89 90 91 plt.title("Model with L2-regularization") 92 axes = plt.gca() 93 axes.set_xlim([-0.75,0.40]) 94 axes.set_ylim([-0.75,0.65]) 95 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
预测准确率0.93

Dropout正则化(随机失活)
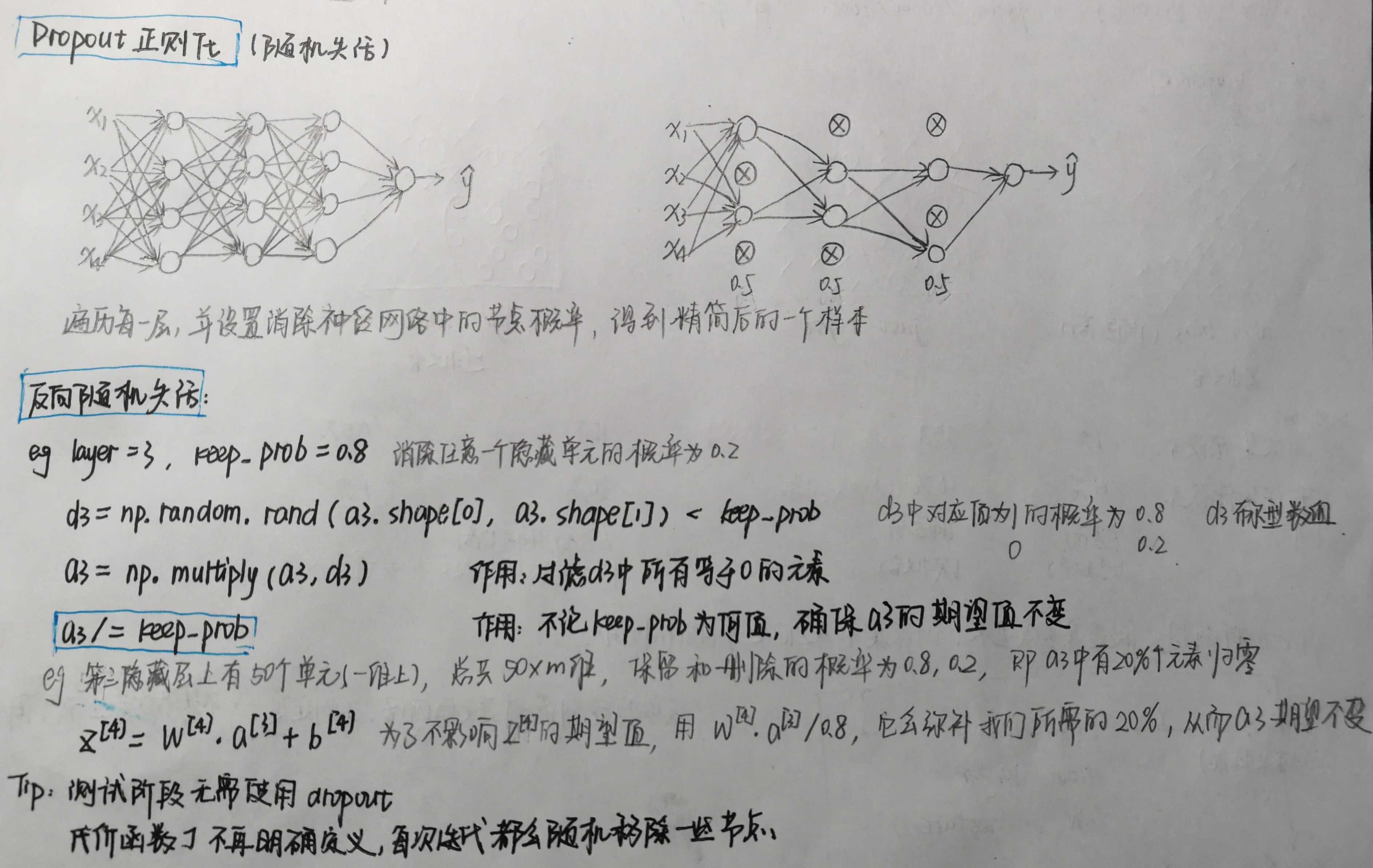

1 # GRADED FUNCTION: forward_propagation_with_dropout 2 def forward_propagation_with_dropout(X, parameters, keep_prob=0.5): 3 """ 4 Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID. 5 6 Arguments: 7 X -- input dataset, of shape (2, number of examples) 8 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 9 W1 -- weight matrix of shape (20, 2) 10 b1 -- bias vector of shape (20, 1) 11 W2 -- weight matrix of shape (3, 20) 12 b2 -- bias vector of shape (3, 1) 13 W3 -- weight matrix of shape (1, 3) 14 b3 -- bias vector of shape (1, 1) 15 keep_prob - probability of keeping a neuron active during drop-out, scalar 16 17 Returns: 18 A3 -- last activation value, output of the forward propagation, of shape (1,1) 19 cache -- tuple, information stored for computing the backward propagation 20 """ 21 np.random.seed(1) 22 23 # retrieve parameters 24 W1 = parameters["W1"] 25 b1 = parameters["b1"] 26 W2 = parameters["W2"] 27 b2 = parameters["b2"] 28 W3 = parameters["W3"] 29 b3 = parameters["b3"] 30 31 # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID 32 Z1 = np.dot(W1, X) + b1 33 A1 = relu(Z1) 34 ### START CODE HERE ### (approx. 4 lines) # Steps 1-4 below correspond to the Steps 1-4 described above. 35 D1=np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...) 36 D1=D1<keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold) 37 A1=np.multiply(A1,D1) # Step 3: shut down some neurons of A1 38 A1/=keep_prob # Step 4: scale the value of neurons that haven't been shut down 39 ### END CODE HERE ### 40 41 Z2 = np.dot(W2, A1) + b2 42 A2 = relu(Z2) 43 ### START CODE HERE ### (approx. 4 lines) 44 D2=np.random.rand(A2.shape[0], A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...) 45 D2=D2<keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold) 46 A2=np.multiply(A2,D2) # Step 3: shut down some neurons of A2 47 A2/=keep_prob # Step 4: scale the value of neurons that haven't been shut down 48 ### END CODE HERE ### 49 50 Z3 = np.dot(W3, A2) + b3 51 A3 = sigmoid(Z3) 52 53 cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) 54 return A3, cache 55 56 X_assess, parameters = forward_propagation_with_dropout_test_case() 57 A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob=0.7) 58 print ("A3 = " + str(A3)) 59 60 61 # GRADED FUNCTION: backward_propagation_with_dropout 62 def backward_propagation_with_dropout(X, Y, cache, keep_prob): 63 """ 64 Implements the backward propagation of our baseline model to which we added dropout. 65 66 Arguments: 67 X -- input dataset, of shape (2, number of examples) 68 Y -- "true" labels vector, of shape (output size, number of examples) 69 cache -- cache output from forward_propagation_with_dropout() 70 keep_prob - probability of keeping a neuron active during drop-out, scalar 71 72 Returns: 73 gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables 74 """ 75 76 m = X.shape[1] 77 (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache 78 79 dZ3 = A3 - Y 80 dW3 = 1. / m * np.dot(dZ3, A2.T) 81 db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True) 82 83 dA2 = np.dot(W3.T, dZ3) 84 ### START CODE HERE ### (≈ 2 lines of code) 85 dA2 = dA2*D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation 86 dA2 = dA2/keep_prob # Step 2: Scale the value of neurons that haven't been shut down 87 ### END CODE HERE ### 88 89 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 90 dW2 = 1. / m * np.dot(dZ2, A1.T) 91 db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True) 92 93 dA1 = np.dot(W2.T, dZ2) 94 ### START CODE HERE ### (≈ 2 lines of code) 95 dA1=dA1*D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation 96 dA1=dA1/keep_prob # Step 2: Scale the value of neurons that haven't been shut down 97 ### END CODE HERE ### 98 99 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 100 dW1 = 1. / m * np.dot(dZ1, X.T) 101 db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True) 102 103 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2, 104 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 105 "dZ1": dZ1, "dW1": dW1, "db1": db1} 106 107 return gradients 108 109 110 X_assess, Y_assess, cache = backward_propagation_with_dropout_test_case() 111 gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob=0.8) 112 print ("dA1 = " + str(gradients["dA1"])) 113 print ("dA2 = " + str(gradients["dA2"])) 114 115 116 parameters = model(train_X, train_Y, keep_prob=0.86, learning_rate=0.3) 117 print("On the train set:") 118 predictions_train = predict(train_X, train_Y, parameters) 119 print("On the test set:") 120 predictions_test = predict(test_X, test_Y, parameters) 121 122 123 plt.title("Model with dropout") 124 axes = plt.gca() 125 axes.set_xlim([-0.75, 0.40]) 126 axes.set_ylim([-0.75, 0.65]) 127 plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
预测准确度0.95

梯度校验

一维梯度校验:

1 from testCases_v3 import gradient_check_n_test_case 2 from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector 3 4 #一维梯度校验 5 # GRADED FUNCTION: forward_propagation 6 def forward_propagation(x, theta): 7 """ 8 Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x) 9 10 Arguments: 11 x -- a real-valued input 12 theta -- our parameter, a real number as well 13 14 Returns: 15 J -- the value of function J, computed using the formula J(theta) = theta * x 16 """ 17 18 ### START CODE HERE ### (approx. 1 line) 19 J = np.dot(theta, x) 20 ### END CODE HERE ### 21 return J 22 23 x, theta = 2, 4 24 J = forward_propagation(x, theta) 25 print ("J = " + str(J)) 26 27 28 # GRADED FUNCTION: backward_propagation 29 def backward_propagation(x, theta): 30 """ 31 Computes the derivative of J with respect to theta (see Figure 1). 32 33 Arguments: 34 x -- a real-valued input 35 theta -- our parameter, a real number as well 36 37 Returns: 38 dtheta -- the gradient of the cost with respect to theta 39 """ 40 ### START CODE HERE ### (approx. 1 line) 41 dtheta=x 42 ### END CODE HERE ### 43 return dtheta 44 45 x, theta = 2, 4 46 dtheta = backward_propagation(x, theta) 47 print ("dtheta = " + str(dtheta)) 48 49 50 # GRADED FUNCTION: gradient_check 51 def gradient_check(x, theta, epsilon=1e-7): 52 """ 53 Implement the backward propagation presented in Figure 1. 54 55 Arguments: 56 x -- a real-valued input 57 theta -- our parameter, a real number as well 58 epsilon -- tiny shift to the input to compute approximated gradient with formula(1) 59 60 Returns: 61 difference -- difference (2) between the approximated gradient and the backward propagation gradient 62 """ 63 64 # Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit. 65 ### START CODE HERE ### (approx. 5 lines) 66 theta1=theta+epsilon # Step 1 67 theta2=theta-epsilon # Step 2 68 J1=forward_propagation(x, theta1) # Step 3 69 J2=forward_propagation(x, theta2) # Step 4 70 gradapprox=(J1-J2)/(2*epsilon) # Step 5 71 ### END CODE HERE ### 72 73 # Check if gradapprox is close enough to the output of backward_propagation() 74 ### START CODE HERE ### (approx. 1 line) 75 grad = backward_propagation(x, theta) 76 ### END CODE HERE ### 77 78 ### START CODE HERE ### (approx. 1 line) 79 numerator = np.linalg.norm(grad - gradapprox) # Step 1' 80 denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2' 81 difference = numerator / denominator # Step 3' 82 ### END CODE HERE ### 83 84 if difference < 1e-7: 85 print("The gradient is correct!") 86 else: 87 print("The gradient is wrong!") 88 89 return difference 90 91 x, theta = 2, 4 92 difference = gradient_check(x, theta) 93 print("difference = " + str(difference))
输出:
The gradient is correct!
difference = 2.919335883291695e-10
N维梯度校验:

1 #N维梯度校验 2 def forward_propagation_n(X, Y, parameters): 3 """ 4 Implements the forward propagation (and computes the cost) presented in Figure 3. 5 6 Arguments: 7 X -- training set for m examples 8 Y -- labels for m examples 9 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 10 W1 -- weight matrix of shape (5, 4) 11 b1 -- bias vector of shape (5, 1) 12 W2 -- weight matrix of shape (3, 5) 13 b2 -- bias vector of shape (3, 1) 14 W3 -- weight matrix of shape (1, 3) 15 b3 -- bias vector of shape (1, 1) 16 17 Returns: 18 cost -- the cost function (logistic cost for one example) 19 """ 20 21 # retrieve parameters 22 m = X.shape[1] 23 W1 = parameters["W1"] 24 b1 = parameters["b1"] 25 W2 = parameters["W2"] 26 b2 = parameters["b2"] 27 W3 = parameters["W3"] 28 b3 = parameters["b3"] 29 30 # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID 31 Z1 = np.dot(W1, X) + b1 32 A1 = relu(Z1) 33 Z2 = np.dot(W2, A1) + b2 34 A2 = relu(Z2) 35 Z3 = np.dot(W3, A2) + b3 36 A3 = sigmoid(Z3) 37 38 # Cost 39 logprobs = np.multiply(-np.log(A3), Y) + np.multiply(-np.log(1 - A3), 1 - Y) 40 cost = 1. / m * np.sum(logprobs) 41 42 cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) 43 44 return cost, cache 45 46 47 def backward_propagation_n(X, Y, cache): 48 """ 49 Implement the backward propagation presented in figure 2. 50 51 Arguments: 52 X -- input datapoint, of shape (input size, 1) 53 Y -- true "label" 54 cache -- cache output from forward_propagation_n() 55 56 Returns: 57 gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables. 58 """ 59 60 m = X.shape[1] 61 (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache 62 63 dZ3 = A3 - Y 64 dW3 = 1. / m * np.dot(dZ3, A2.T) 65 db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True) 66 67 dA2 = np.dot(W3.T, dZ3) 68 dZ2 = np.multiply(dA2, np.int64(A2 > 0)) 69 dW2 = 1. / m * np.dot(dZ2, A1.T) * 2 # Should not multiply by 2 70 db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True) 71 72 dA1 = np.dot(W2.T, dZ2) 73 dZ1 = np.multiply(dA1, np.int64(A1 > 0)) 74 dW1 = 1. / m * np.dot(dZ1, X.T) 75 db1 = 4. / m * np.sum(dZ1, axis=1, keepdims=True) # Should not multiply by 4 76 77 gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, 78 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2, 79 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1} 80 81 return gradients 82 83 84 # GRADED FUNCTION: gradient_check_n 85 def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7): 86 """ 87 Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n 88 89 Arguments: 90 parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3": 91 grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. 92 x -- input datapoint, of shape (input size, 1) 93 y -- true "label" 94 epsilon -- tiny shift to the input to compute approximated gradient with formula(1) 95 96 Returns: 97 difference -- difference (2) between the approximated gradient and the backward propagation gradient 98 """ 99 100 # Set-up variables 101 parameters_values, _ = dictionary_to_vector(parameters) 102 grad = gradients_to_vector(gradients) 103 num_parameters = parameters_values.shape[0] 104 J_plus = np.zeros((num_parameters, 1)) 105 J_minus = np.zeros((num_parameters, 1)) 106 gradapprox = np.zeros((num_parameters, 1)) 107 108 # Compute gradapprox 109 for i in range(num_parameters): 110 111 # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]". 112 # "_" is used because the function you have to outputs two parameters but we only care about the first one 113 ### START CODE HERE ### (approx. 3 lines) 114 theta1=np.copy(parameters_values) # Step 1 115 theta1[i][0]+=epsilon # Step 2 116 J_plus[i],_=forward_propagation_n(X, Y, vector_to_dictionary(theta1)) # Step 3 117 ### END CODE HERE ### 118 119 120 # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]". 121 ### START CODE HERE ### (approx. 3 lines) 122 theta2=np.copy(parameters_values) # Step 1 123 theta2[i][0]-=epsilon # Step 2 124 J_minus[i],_=forward_propagation_n(X, Y, vector_to_dictionary(theta2)) # Step 3 125 ### END CODE HERE ### 126 127 # Compute gradapprox[i] 128 ### START CODE HERE ### (approx. 1 line) 129 gradapprox[i]=(J_plus[i]-J_minus[i])/(2*epsilon) 130 ### END CODE HERE ### 131 132 # Compare gradapprox to backward propagation gradients by computing difference. 133 ### START CODE HERE ### (approx. 1 line) 134 numerator = np.linalg.norm(grad - gradapprox) # Step 1' 135 denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2' 136 difference = numerator / denominator # Step 3' 137 ### END CODE HERE ### 138 139 if difference > 1e-7: 140 print("�33[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "�33[0m") 141 else: 142 print("�33[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "�33[0m") 143 144 return difference 145 146 147 X, Y, parameters = gradient_check_n_test_case() 148 149 cost, cache = forward_propagation_n(X, Y, parameters) 150 gradients = backward_propagation_n(X, Y, cache) 151 difference = gradient_check_n(parameters, gradients, X, Y)
输出:
There is a mistake in the backward propagation! difference = 0.2850931566540251
