要建立一个数组,首先需要一个维数向量dim来描述其维数属性. dim 是由一个或多个非负整数组成的向量,所有非负整数的乘积等于数组的长度。一个向量只有定义其维数以后才能成为一个数组,例如:
x<-c(1:10) is.array(x)#检验x是不是数组 is.vector(x)#查看其是不是一个向量 dim(x)<-8#定义谁数后成为数组 dim(x)<-10#定义谁数后成为数组,且长度要与向量长度一样 is.array(x)#检验x是不是数组
结果:

注意:若dim(x)<-8,这个所赋的值已经小于向量的长度,系统会报错为下所示
Error in dim(x) <- 8 :
dims [product 8] do not match the length of object [10]
dim(x)#查看x的数组长度

矩阵的建立:
由于矩阵具有特殊性,R语言中往往利用函数matrix()建立矩阵,利用函数diag()建立对角矩阵.函数matrix()的调用格式为:
matrix(data=NA, nrow = 1, ncol = 1, byrow = FALSE, dimnames= NULL)
其中,data 为给定的数据向量;nrow为矩阵的行数;ncol为矩阵的列数;;byrow 为逻辑参数,默认状态为FALSE,即按列填充数据; dimnames 为矩阵维数的名称,默认时为空。例如
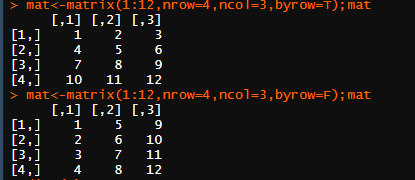
mat<-matrix(1:12,nrow=4,ncol=3,byrow=T);mat
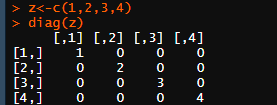
diag(4)#创建一个4阶的单位矩阵

z<-c(1,2,3,4)#创建一个主对角线上的元素为z向量上的这些元素的矩阵 diag(z)#创建矩阵
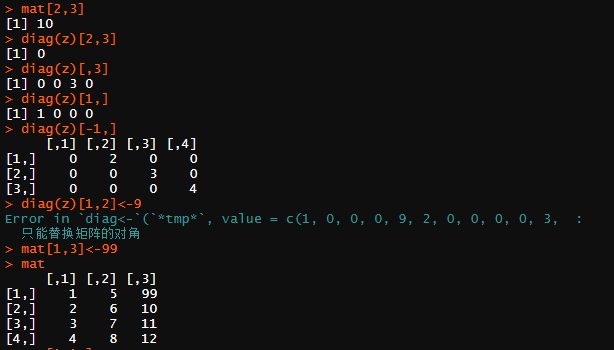
mat[2,3]#查看矩阵第二行第三列的元素 diag(z)[,3]#查看矩阵z的第三列元素 diag(z)[1,]#查看矩阵z的第一行上的元素 diag(z)[-1,]#去除矩阵z的第一行元素 mat[1,3]<-99;mat#替换第一行第三列位置上的元素
mat[1+1,]#第一行元素+1

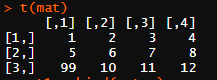
t(mat)#转置
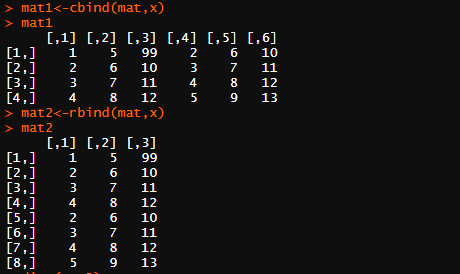
mat1<-cbind(mat,x);mat1#按列合并矩阵
mat2<-rbind(mat,x);mat2#按行合并矩阵
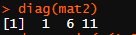
diag(mat2)#查看矩阵主对角线上的元素
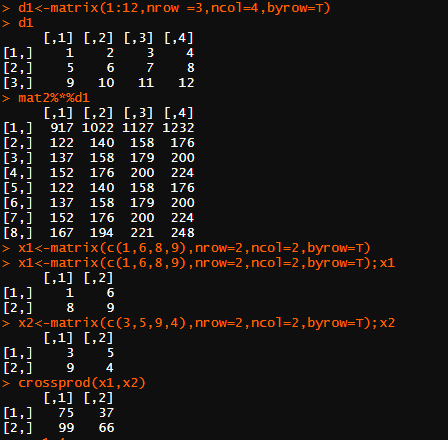
d<-matrix(c(1,3,6,9),nrow=2,ncol=2);d#建一个方阵

det(d)#计算方阵的行列式值

矩阵的代数乘积:矩阵A和B的代数乘积A%*%B只有在A的列数与矩阵B的行数相同的条件下才能够进行运算.。
矩阵A和B的交叉乘积:

矩阵(向量)的外积

线性方程组的求解

矩阵的特征值与特征向量

矩阵的奇异值分解

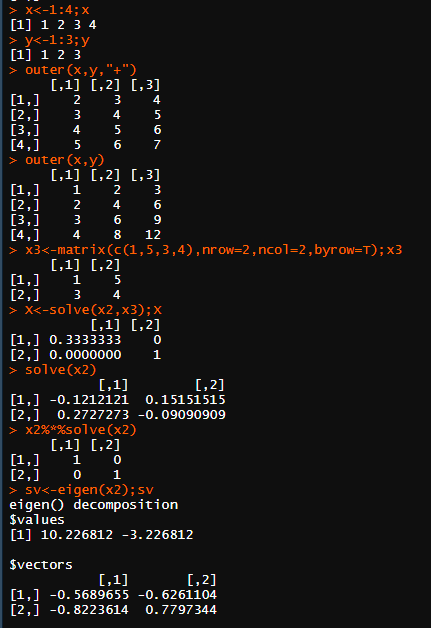
d1<-matrix(1:12,nrow =3,ncol=4,byrow=T);d1#创建矩阵 mat2%*%d1#两个矩阵的乘积 x1<-matrix(c(1,6,8,9),nrow=2,ncol=2,byrow=T);x1#创建矩阵 x2<-matrix(c(3,5,9,4),nrow=2,ncol=2,byrow=T);x2#创建矩阵 crossprod(x1,x2)#内积 x<-1:4;x y<-1:3;y outer(x,y,"+")#外积 outer(x,y)#外积 x3<-matrix(c(1,5,3,4),nrow=2,ncol=2,byrow=T);x3#矩阵 X<-solve(x2,x3);X#求出X的值 solve(x2)#由于矩阵x2可逆,则命令solve(x2)返回矩阵x2的逆矩阵
x2%*%solve(x2)#证明solve(x2)是x2的逆矩阵
sv<-eigen(x2);sv#特征值与特征向量
a1<-matrix(c(-1,2,3,1,0,3,-2,1,4,0,3,2),nrow=3,ncol=4,byrow=T);a1 b1<-matrix(c(4,3,2,-1,5,-3,0,1,1,2,-5,0),nrow=3,ncol=4,byrow=T);b1 3*a1-2*b1#3a1-2b1的值 A<-matrix(c(3,-1,2,0,1,5,7,9,2,4,6,8),nrow=3,ncol = 4,byrow = T);A B<-matrix(c(7,5,-2,4,5,1,9,7,3,2,-1,6),nrow=3,ncol=4,byrow=T);B x<-((B-A)/2);x#求解A-2X=B的值 C<-matrix(1:12,nrow=3,ncol=4,byrow=T);C svd(C)#求出其的奇异值
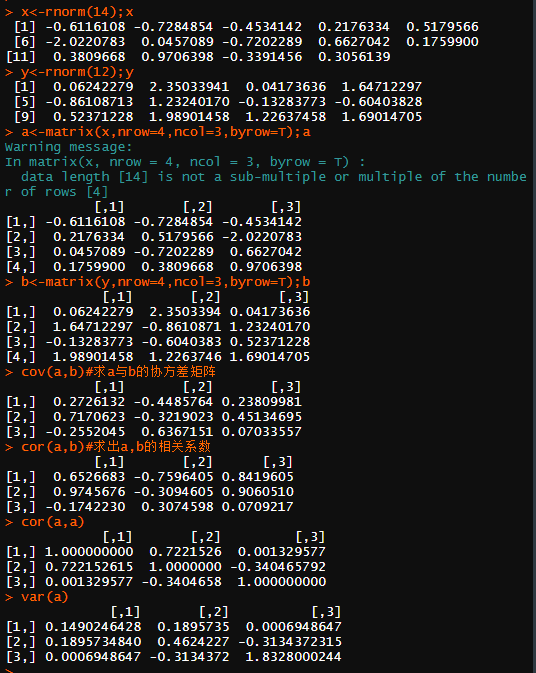
函数max(、min()、median(、 sumO、mean(、 sd0分别返回矩阵所有元素的最大值、最小值、中位数、和、均值以及标准差; var(A)返 回矩阵A的各列的协方差阵; cov(A,B)和cor(A,B)分别返回矩阵A和矩阵B的各列的协方差阵和相关系数阵,由定义cov(a,a)=var(a)。
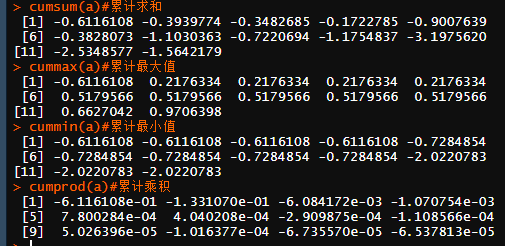
函数cumsum(、cumprod0、 cummax(、 cummin0分别返回矩阵的(按列)累积求和、累积乘积、累积最大值以及累积最小值向量。
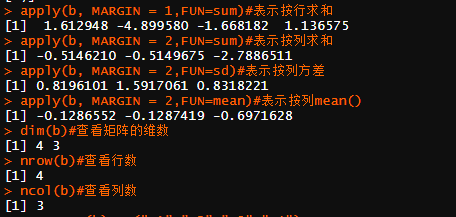
函数max(、min(、 median(、sum()、mean(、 sd0只针对矩阵所有元素计算,若针对每一行或每一列进行 上述计算,可以利用命令apply0),其调用格式为:
apply(X, MARGIN, FUN)
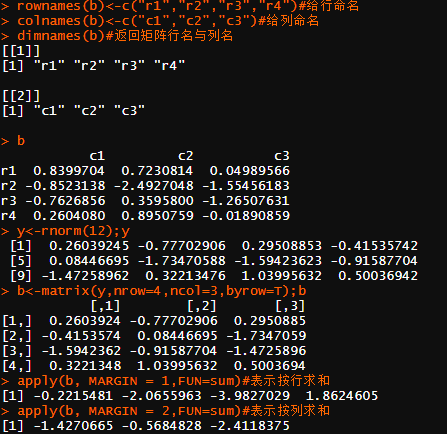
其中,X为矩阵或数组; FUN为上述函数;当X为矩阵时,参数MARGIN=1,表示按行计算,MARGIN=2,表示按列计算,当X为三维数组时,MARGIN=c(1, 2)表示按行列进行等,另外,函数dim()、 nrow()以及ncol()可以分别得到矩阵的维数、行数和列数,rownames()、colnames()给矩阵分别添加行名和列名; dimnames()返回矩阵的行名和列名。


.