T1
1.聪明的小偷
(thief.pas/c/cpp)
【问题描述】
从前有一个收藏家收藏了许多相同的硬币,并且将它们放在了n个排成一排的口袋里,每个口袋里都装了一定数量的硬币。
这些硬币价值不菲,自然引起不少人觊(ji,4)觎(yu,2),于是收藏家每天都会来检查一次这n个口袋,首先他会先检查每个口袋是不是都有硬币,之后他会计算出第1个和第2个口袋的硬币数量之和,第2个与第3个口袋的硬币数量和,如此直到第n-1个与第n个口袋的硬币数量之和,得到n-1个数的序列。
如果收藏家发现某个口袋没有硬币,或者他计算得到的序列较上一天相比有变动,那么收藏家就知道肯定有人动了他的硬币。
有一个聪明的小偷,他想在收藏家不知道的情况下偷走一些硬币,为此,他不仅可以偷偷地从某个口袋中拿出一些硬币,也可以将硬币在口袋间任意移动,现在他想知道对于给定的n个口袋及对应的硬币数量,他最多能拿多少枚硬币。
小偷是很聪明的,他早就算出来啦,但是他想考考作为徒弟的你……
【数据规模与约定】
对于50%的数据,有2≤n≤20,每个口袋中硬币数量≤20。
对于100%的数据,有2≤n≤999,每个口袋中硬币数量≤10000且为正整数。
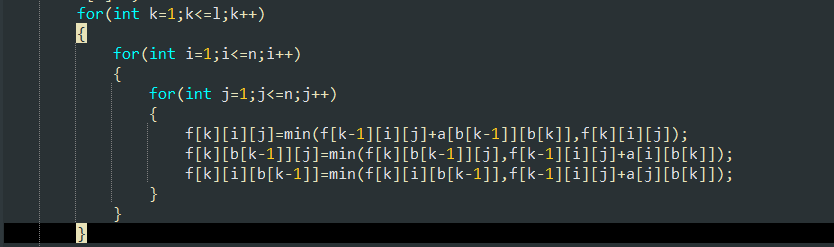
贪心提,自己造了几组数据,连蒙带猜找到规律就可以了
当n为偶数时,答案一定为 0,当 n为奇数时,答案为所有编号为奇数的口袋中硬币数量的最小值 -1。
注:n<=3时奇数也不行
T2
2.无名
(noname.pas/c/cpp)
【问题描述】
这道题实在不知道该取什么名字比较好,于是就取了这个名字。
给定一个长度为n的正整数序列,你的任务就是求出至少需要修改序列中的多少个数才能使得该数列成为一个严格(即不允许相等)单调递增的正整数序列,对序列中的任意一个数,你都可以将其修改为任意的正整数。
【数据规模与约定】
对于30%的数据,有1≤n≤10。
对于80%的数据,有1≤n,T≤50,且输入序列中每个数均不超过50。
对于100%的数据,有1≤n≤50000,1≤T≤5000,输入序列中每个数均为不超过1000000000(10^9)的正整数,且每个测试点中T组数据对应的n值总和不超过500000。
看到数据范围就果断选择80分算法
80分:
DP
f[i][j] 代表前i个数最后一位为j时的最小改变策略

x 表示可以任意数变到的最大值
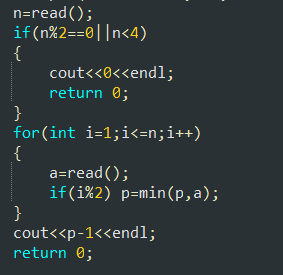
正解:
简单来说就是:构造序列b[i] = a[i] – i;答案即为序列总长度减去B的最长不下降子序列。
(nlogn)二分优化lis
T3
3.服务
(service.pas/c/cpp)
【问题描述】
一家公司为它在各地的用户提供服务,公司有三名负责这项工作的员工,分别编号为1,2,3,服务的地点有n个,分别编号为1,2,3,...n,把从编号为p的服务地点直接到达编号为q的服务地点所需的移动费用记为C(p,q),显然C(p,p)=0(停留在原地不需要费用),但不保证对任意p,q均有C(p,q)=C(q,p)。
初始时员工1在地点1,员工2在地点2,员工3在地点3,现在公司依次收到了L个服务请求,每个请求需要一名员工赶到其指定的地点进行服务,员工可以选择直达,也可以选择经过若干个服务地点中转,特别地,如果指派的员工已在当前请求所在地,则该请求不需要任何移动费用即可被处理。
出于公平起见,所有请求必须按顺序处理,这意味着即使一名员工在赶往当前请求的途中经过之后的请求所在的地点,他也不可以先处理之后的请求,但是公司不限制每位员工赶往请求地点的路线,也允许一个服务地点有多名员工。
你的任务就是对于这L个请求,找到一个服务方案(即对每个请求分配合适的员工去服务以及规划移动路线),使得三名员工提供服务的总移动费用最小。
【数据规模与约定】
每个测试点5分,各个测试点数据范围如下:
|
测试点编号 |
n |
L |
|
1-3 |
||
|
4-6 |
||
|
7-10 |
||
|
11-14 |
||
|
15-17 |
||
|
18-20 |
对于所有的测试点,均有数据组数,地点数,给定的C矩阵主对角线上的数全部为0,且输入数据中所有的数均为不超过2000的非负整数。
从考试开始到结束都没想过4维的DP
打了不知道多长时间的暴力后 果断放弃提交()
正解:
首先用Floyd求最短路。
4 维 DP f[k][i1][i2][i3] 代表做到第 k 个任务是3人在 i1 i2 i3 时的费用。
5重循环。
优化
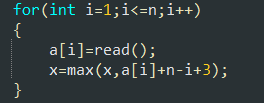
因为有任务,所以可已确定完成这个任务前后某个人的位置 完成第 k 个任务前一定有一个人在 b[k1-1] 的位置 完成第 k 个任务后一定有一个人在 p[k1] 的位置。所以就能剩一冲循环了(4重)。
因为可以确定某个人的位置,所以可以再省略一维 i3。i1,i2都不到p[k1]的位值,i3一定就在;i1或 i2到 b[k1]的位值,i3一定就不在;
所以:并列3个核心
注:初始化f[0][1][2]=0;
b[0]=3;